温度对电纺聚氨酯纳米纤维机械性能的影响

背景

一维 (1D) 纳米材料由于其独特的性质和在许多领域的有趣应用而得到深入研究 [1,2,3]。已经探索了许多合成和制造方法，以从各种材料中生成纤维、线、棒和管形式的一维纳米结构 [4, 5]。然而，它们的用途受到受限材料范围、成本和生产率的组合的限制。与其他产生一维纳米结构的方法不同，静电纺丝具有成本相对较低和生产率高的优势，除了使用静电排斥来不断减小粘弹性射流的直径外，这与生产微米级纤维的商业工艺相似。 6, 7]。

聚氨酯 (PU) 由通过氨基甲酸酯键连接的软段和硬段组成，其中软段赋予柔韧性，而硬段提供刚度和强度 [8, 9]。 PU 材料在工业中得到了广泛的应用，因为它的硬度可以通过改变结构中的硬段来轻松调节 [10]。静电纺 PU 纳米纤维在高性能空气过滤器、防护纺织品、伤口敷料薄膜和传感器中具有广泛的潜在应用 [11, 12]。了解机械性能对于纳米材料的应用和功能至关重要 [13]。然而，由于难以进行纳米级测试，对电纺纳米纤维机械性能的研究很少受到关注。在过去的十年中，原子力显微镜 (AFM) 被用来以一种直接的方式表征一维纳米结构的机械性能 [14,15,16]。一种基于 AFM 的简便三点弯曲测试旨在测量单个纳米纤维的杨氏模量，该测试涉及通过样品和基板之间的自粘力将一维纳米结构夹持在沟槽上。悬浮的一维纳米结构的中点受到 AFM 尖端施加的力，然后，记录中点的相应偏转并用于计算杨氏模量。在这里，PU 纳米纤维是通过静电纺丝法制备的。然后通过三点弯曲试验研究了温度对聚氨酯纳米纤维杨氏模量的影响。

方法

材料准备

N, N-二甲基甲酰胺（DMF）和四氢呋喃（THF）购自天津恒兴化学试剂有限公司。聚氨酯弹性体（Elastollan® 1180A10）购自巴斯夫。将 PU 溶解在 DMF 和 THF 的体积比为 1:1 的混合物中。在剧烈搅拌下，将溶液在室温下密封超过 12 小时。市售的静电纺丝装置（北京优卡力科技发展有限公司，中国）用于制造静电纺 PU 纳米纤维。喷嘴和接地收集器之间的距离调整为 13 cm。施加 9-10 kV 的高压以产生聚合物射流。将所得纤维收集在旋转心轴上，在真空条件下放置过夜以去除溶剂残留物，然后保存在干燥器中进行进一步实验。

物理表征和测试方法

通过扫描电子显微镜（SEM，JSM-6610LV，日本）表征所制备的 PU 纳米纤维的微观结构和形态。使用 DSC-TGA（SDT Q600，TA Instruments）在氩气气氛下进行热重差示扫描量热法 (TG/DSC) 分析。电纺PU膜的宏观弹性模量采用万能试验机（Instron 5943，美国）测量。通过使用 Multimode 8 AFM (Bruker Nano Inc., USA) 测试纳米纤维的纳米力学性能。首先，使用Si模板作为收集器（购自苏州RDMICRO有限公司）沉积电纺PU纳米纤维。悬浮在凹槽上的纳米纤维进行了 AFM 测试。基板上凹槽的宽度和深度为2和3 μm。探针被简化为直径为 50 nm 的球体。悬臂的弹簧常数采用热调谐法测量。在蓝宝石表面上校准悬臂的灵敏度，作为悬臂偏转信号与施加的电压的关系。记录力曲线以计算单个纳米纤维的弹性模量。每个实验重复5次，结果取平均值（算术平均值）。进行有限元模拟以评估尖端穿透到纳米纤维表面的程度。在商业软件包（ANSYS 15.0）中建立仿真模型。纳米纤维、探针和基底材料均被视为弹性线性各向同性固体[17]。

结果与讨论

通过SEM和AFM表征了电纺PU纳米纤维的形态特征。如图 1a 所示，电纺 PU 薄膜由随机取向的纳米纤维组成，直径范围从数百纳米到几微米。图 1b 中的 AFM 图像表明 PU 纳米纤维在横向截面中​​是均匀的。 AFM测得的纳米纤维直径为~ 300 nm。

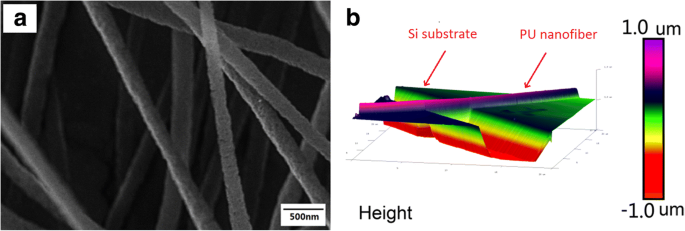
SEM (a ) 和原子力显微镜 (b ) 电纺聚氨酯纳米纤维的图像

图 2a 显示了电纺 PU 纳米纤维在氩气中以 10 °C/min 的加热速率的 TG/DSC 曲线。很明显，聚氨酯纳米纤维在氩气中的热降解表现出一个两阶段的过程。在 100 到 200 °C 之间可以观察到少量的重量损失，表明在此阶段水和一些小分子产物的蒸发。在 300 °C 下观察到的重量损失与聚合物的分解有关 [18, 19]。然而，在氩气中只显示了一个小的吸热峰，对应于主要的失重阶段。如图 2b 所示，电纺 PU 的 FTIR 光谱在 3320、2960、1710、1530、1220、1110 和 777 cm ^-1 处具有特征吸收带 , 代表 υ (N–H), υ (C–H), υ (C–O), υ (C–C), υ (C–C), υ (C–O) 和 υ (C–H), 分别 [18]。

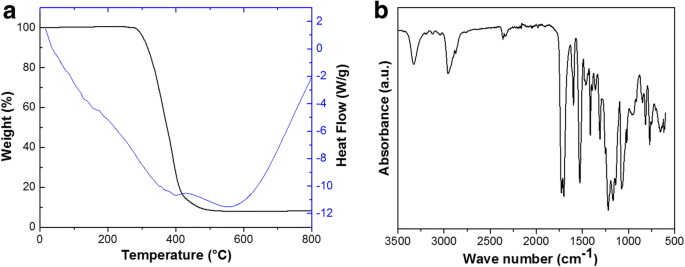
TG/DSC 曲线 (a ) 和 FTIR 光谱 (b )电纺PU纳米纤维

在三点弯曲试验中，PU纳米纤维沉积在Si晶片的表面，如图3所示。两端固定的梁的三点梁弯曲理论已被广泛用于计算a的杨氏模量。纳米纤维如下：

其中 F 是施加在中点的力，L 是纳米纤维的悬浮长度，d 是纳米纤维在中点的挠度，I 是截面惯性矩 (I =πr ⁴ /4，其中 r 是纤维的半径）。计算杨氏模量 [20] 应满足以下假设：(i) 纤维的两端固定，(ii) L 远大于 r , 和 (iii) d 很小。在我们的工作中，在测试中没有观察到纳米纤维和基材之间的相对滑动。得出的结论是L可以将计算误差控制在8%以内。 /r 在之前的工作中大于 10 [17]。因此，在三点弯曲试验期间可以满足这些假设。有限元法模拟结果表明，针尖穿透深度低于纳米纤维变形的10%。因此弹性模量的计算是基于可以忽略表面变形的假设。

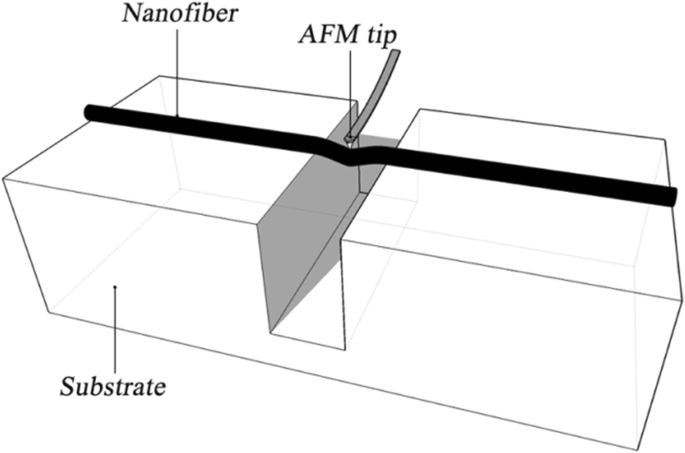
三点弯曲试验方案

图 4a 显示了三点弯曲试验的结果，作为杨氏模​​量与 PU 纳米纤维直径的关系图。单根 PU 纳米纤维的杨氏模量如图所示。 PU 纳米纤维的杨氏模量表现出直径依赖性。模量值随着直径减小到约 300 nm 的特定尺寸以下而增加。 150 nm的直径可以获得~ 25 GPa的高杨氏模量，而直径大于300 nm的杨氏模量降低到~ 5 GPa。在最近的工作中，通过基于 AFM 的三点弯曲试验测量的聚合物纳米纤维如尼龙 6、聚（ε-己内酯）、纤维素和聚乙烯醇的杨氏模量在几 GPa 到几十 GPa 的范围内。 21,22,23]。在这项工作中测量的 PU 纳米纤维的杨氏模量也在上述范围内。还测量了电纺 PU 膜的宏观机械性能。可以获得0.9 MPa的杨氏模量，这可以归因于电纺膜的高孔隙率。

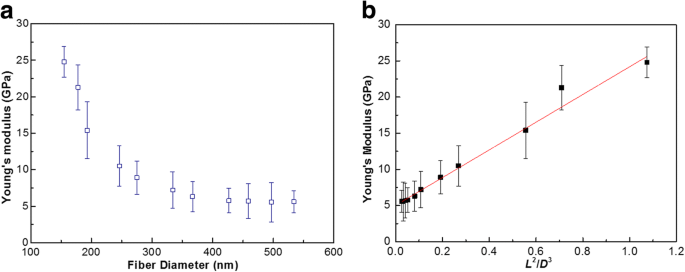
一 杨氏模量与 PU 纳米纤维直径的关系图。 b 表面张力对聚氨酯纳米纤维力学性能的影响

正如之前的工作 [24] 所报道的，观察到的杨氏模量随着直径的减小而增加，主要是由于表面张力效应。考虑表面效应，表观杨氏模量可表示为：

其中 E 0, γ , 和 υ 分别是散装材料的杨氏模量、表面张力和泊松比。 D 是纳米纤维的直径。如图 4b 所示，线性回归允许确定弹性模量和表面张力。因此，PU 纳米纤维的固有杨氏模量约为 ~ 5.0 GPa，远大于散装材料的固有杨氏模量。其原因是在静电纺丝过程中分子链在静电纺丝纤维内取向[25]。

温度对单根 PU 纳米纤维杨氏模量的影响如图 5a 所示。对于直径为 155 nm 的单根 PU 纳米纤维，杨氏模量在 25 °C~ 60 °C 范围内随着温度的升高而线性降低。然而，图 5b 中的 AFM 图像证实，随着温度升高到 60 °C，PU 纳米纤维的纤维形态完全保持不变。横向截面轮廓表明测量的 PU 纳米纤维的直径从 200 到 214 nm 略有增加。我们可以得出结论，PU 纳米纤维在相对较低的温度下具有高尺寸稳定性。此外，杨氏模量与温度的线性关系表明电纺PU纳米纤维在纳米器件和纳米传感器领域的潜在应用。

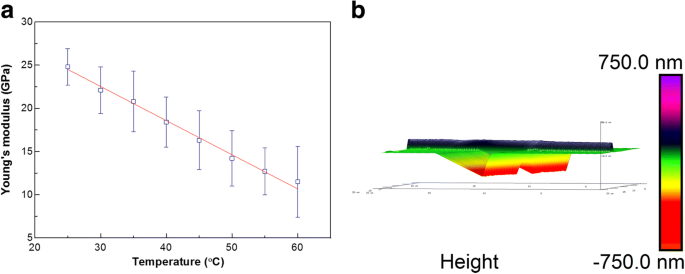
一 温度对单根 PU 纳米纤维杨氏模量的影响。 b 60 °C下单根PU纳米纤维的形貌

单根直径为 215 nm 的 PU 纳米纤维的力学性能退化如图 6 所示。对相同的纳米纤维重复三点弯曲试验 50 次循环。纳米纤维的杨氏模量值略有波动，因为这样的过程不能每次都精确控制在同一点。一般来说，经过50 次循环后，PU纳米纤维表现出良好的耐久性，杨氏模量没有明显下降。

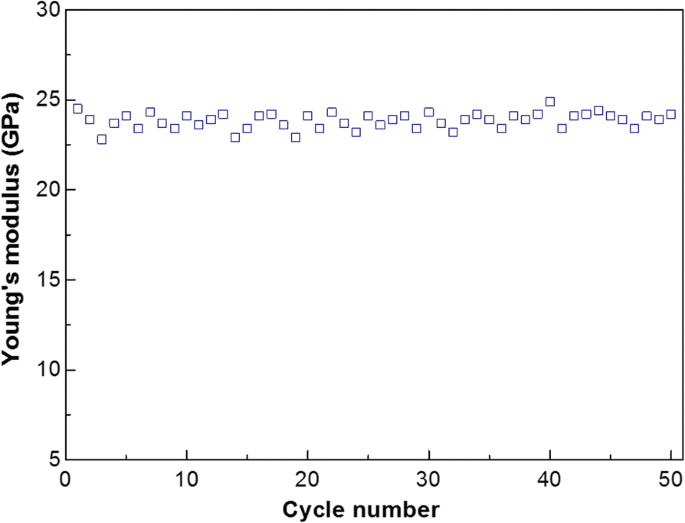
单根聚氨酯纳米纤维力学性能的退化

结论

总之，通过三点弯曲试验测量了由电纺法制备的单根 PU 纳米纤维的杨氏模量。随着直径的减小，杨氏模量增加可以归因于表面效应。此外，杨氏模量在 25 °C~60 °C 范围内随着温度的升高呈线性下降。 PU纳米纤维具有良好的耐久性，即使在50 次循环后杨氏模量也没有明显下降。

缩写

一维：

一维

原子力显微镜：

原子力显微镜

DMF：

N,N-二甲基甲酰胺

PU：

聚氨酯

SEM：

扫描电镜

TGA/DSC：

热重差示扫描量热法（TG/DSC）

THF：

四氢呋喃