石墨烯/金属系统中等离子体诱导的完美吸收

背景

等离子体由于其非凡的特性[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]和在许多领域的巨大潜力而​​受到广泛关注，包括集成光子学、生物传感、能量捕获、光电探测。最近，已经观察到一种新的等离子体现象，称为欺骗表面等离子体 (SSP)，它可以通过穿孔金属传播并克服衍射极限 [16]。然后在太赫兹、微波和较低频率范围内探索了 SSP [17,18,19]，并且已经提出了许多基于 SSP 的深亚波长设备 [20, 21]。然而，SPP 的高阻尼率严重阻碍了此类设备的应用。这个问题的一个解决方案是人工等离子体诱导透明 (PIT) 介质 [22]，它在宽吸收光谱内具有清晰的透明窗口。 PIT 效应主要依赖于辐射元件和亚辐射元件的耦合，这已被广泛研究 [23,24,25]。最近还证明了类似的现象，等离子体诱导吸收 (PIA)，这是由明暗等离子体模式的相长干涉引起的 [26]。 PIA共振[27, 28]可以表现出显着的快光效应，在光开关和处理方面具有潜在的应用前景。

然而，传统的基于金属结构PIA效应的器件很难或不可能获得可调性，严重限制了其应用。石墨烯 [29, 30] 以其半金属性、高迁移率和高可调性而闻名，可以成为可调谐红外等离子体器件的极好候选材料。在本文中，我们研究了可调谐 PIA 效应，该效应是通过分别由周期性银凹槽和单层石墨烯支持的 F-P 共振模式和准导模式的相长干涉实现的。发现谐振强度和线宽强烈依赖于耦合距离。还表明消光率可以达到~ 99.999%。消光比定义为 1-R -T ，其中 R 和 T 分别为反射率和透射率。它只是 1-R 在我们的系统中，因为这里的透射率为 0。因此，超高 FOM* 高达 10 ⁶ 在石墨烯/金属系统中可以实现，并且可以通过调节石墨烯的栅极电压来动态调节谐振频率。这些突出的特性可应用于生化传感和动态光开关。

方法

我们的结构示意图如图 1 所示，由单层石墨烯和位于带槽银顶部的 Al2O3 隔离层组成。 Al2O3 的厚度为 g .该系统由横向磁 (TM) 极化的法向入射平面波照亮。其他结构参数表示如下：d 是银槽的深度； w 是银槽的宽度； P 是晶胞的周期。在中红外区域，带内散射在高掺杂石墨烯中占主导地位，其导电性呈现出类似德鲁德的形式σ g =即 ² E F/[πħ ² (ω +iτ ^-1 )]。电子弛豫时间表示为τ =μE F/eυ F ² , 其中 υ F =c /300 是费米速度，E F 是费米能量，μ =10 米 ² /Vs 是石墨烯的直流迁移率 [25, 31, 32]。在有限差分时域 (FDTD) 模拟中，银和 Al2O3 的光学常数来自参考文献。 [33] 和参考。 [34]。周期边界条件用于模拟无限周期单元结构。为简单起见，我们假设石墨烯层上方区域的材料是真空（ε 0 =1).

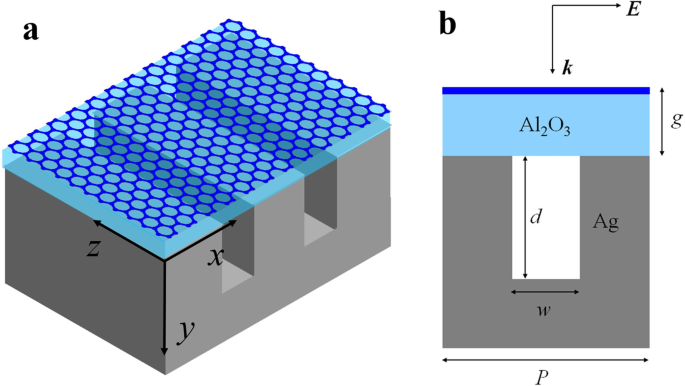
石墨烯-银槽结构示意图。 一 斜视。 b 一个晶胞的横截面图

结果与讨论

我们用w模拟了银槽的反射光谱 =100 纳米，P =250 纳米，d =2000 nm，结果如图 2a（红色曲线）所示。在 ~ 28 THz 处可以观察到一个大的下降，消光比 ~ 44% 和 Q 因子 ~ 0.8，这是由于由入射光激发的 SSP 引起的 F-P 共振[19]。这种共振具有广泛的共振带，因此共振模式可以作为我们 PIA 系统中的超辐射模式。然后，我们计算了模拟区域底部具有金属边界条件的石墨烯片的反射光谱，费米能级E F =0.3 eV，如图 2a（蓝色曲线）所示。反射光谱表明，石墨烯等离子体共振不能被该频率的入射直接激发。为了可视化和优化石墨烯支持的等离子体模式，我们首先模拟石墨烯支持的共振模式。为了消除银凹槽 F-P 共振的潜在影响，我们假设凹槽由硅而不是银制成。计算结构的反射光谱对于E F =0.3 eV 和不同的晶胞 P 并如图 2b 所示。谐振频率 f 处的反射率下降 =32.84 THz 可以观察到 P =250 纳米，Q 因子 ~ 304. 高 Q 具有窄共振带的共振可以作为我们 PIA 系统中的亚辐射（暗）模式。反射率下降是由于石墨烯中等离子体准导模与法向入射的共振 [35] 因为凹槽可以补偿基于 m 的波矢失配 三阶相位匹配条件[36, 37]

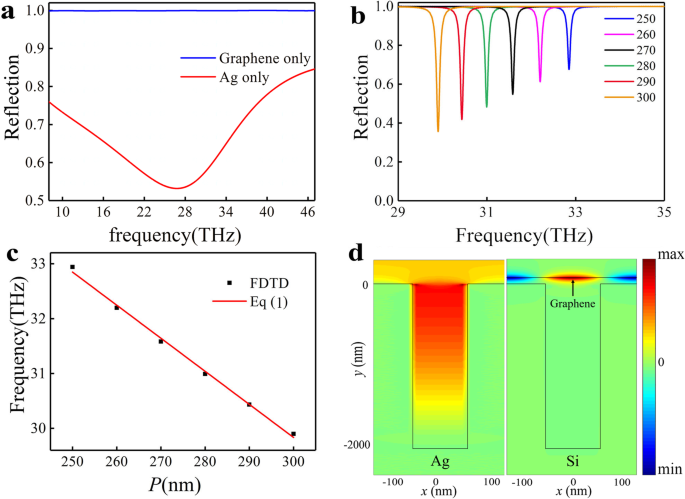
单模的光学响应。 一 分别为纯银槽结构（红线）和纯石墨烯（蓝线）结构在垂直入射时的反射光谱。 b 不同周期P下石墨烯-Si凹槽结构的反射光谱 单元格的。 c 谐振频率f的数值模拟与解析结果 ， 分别。 d 电场E F-P模式（左）和石墨烯准导谐振模式（右）的x分布。

其中 k x =k 0sinθ , k 0 =2π /λ 是自由空间中的波矢，θ 是入射光与y之间的夹角 -方向，n eff 是石墨烯中 TM 波导模式的有效折射率，G x 是光栅的倒格向量 (G x =2π /P ）。在下面的讨论中，y的入射光角 -方向为零（θ =0°）。其他入射角的情况在附加文件 1 中讨论。这些反射下降的位置对应于石墨烯中准导模的共振频率，如图 2b 所示。仿真结果与方程非常吻合。 (1), 其中 m =1，有效折射率 ~ 33，是通过 FDTD 解决方案获得的，如图 2c 所示。电场E F-P模式和石墨烯准导模式的x分布如图2d所示。值得注意的是，与石墨烯准导模相比，Si凹槽表面所承受的SSP模式的能量限制可以忽略不计。

在耦合情况下，两个本征模在彼此靠近时会强烈耦合，因此反射光谱将发生显着变化。如图 3a 所示，在更宽的反射率下降的顶部观察到了一个狭窄的亚线宽下降，吸光度增强，消光比 ~ 99.97%。当增加垂直距离 g ，近场耦合和准导模变弱，因为反射倾角的调制变小。有两种可能的方式导致反射率下降较小，即较弱的耦合和较弱的准导模激发。因此，我们采用耦合振荡器模型来定量理解PIA系统[38]。

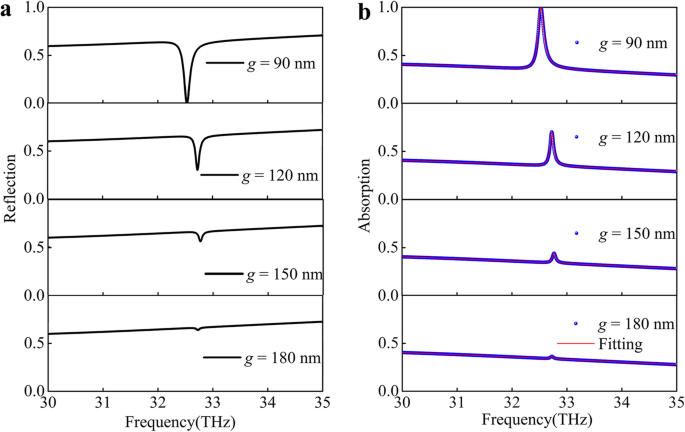
光学响应随耦合距离而变化。 一 反射。 b 不同距离g垂直入射石墨烯-银槽结构的吸收光谱 石墨烯和银槽之间。黑色曲线/蓝色球是通过 FDTD 方法计算的，红色曲线是通过方程解析拟合的。 (3)PIA设备

其中 \( {\tilde{a}}_{1,2}={a}_{1,2}\left(\omega \right){\mathrm{e}}^{i\omega t} \) , ω 1,2 和 γ 1,2 分别是亮模式和暗模式的时谐振幅、谐振频率和阻尼常数。 b 是测量亮模与入射电场耦合强度的耦合系数。 \( \tilde{\kappa}=\kappa {e}^{i\varphi} \) 是一个复杂的耦合参数，引入它来表达相位延迟效应。 φ 是相移，是决定两条相干路径间干扰形式的关键系数。当φ =0 是一个实参数，可以观察到 PIT 效应的典型行为，两个相干路径之间的干扰是破坏性的。对于φ =π/2 是纯虚参数，两条相干路径之间的干扰从破坏性转换为建设性 [26]。系统的吸收可以根据公式（2）计算为耗散的能量，即

$$ A\left(\omega \right)=\Im \left(\frac{b\left(\omega -{\omega}_2+\frac{i{\gamma}_2}{2}\right)}{ \kappa^2{e}^{i2\varphi }-\left(\omega -{\omega}_1+\frac{i{\gamma}_1}{2}\right)\left(\omega -{\omega }_2+\frac{i{\gamma}_2}{2}\right)}\right) $$ (3)

然后，我们用方程拟合数值吸收光谱。 (3) 对于不同的g ，如图 3b（红色曲线）所示。仿真结果与基于耦合振荡器模型的分析建模结果非常吻合，有力地证实了我们 PIA 器件的设计原理。拟合参数κ , φ , γ 1、γ 2 已显示在图 4a-c 中。增加的 g 导致耦合参数 κ 降低 ，如图 4a 所示。当逐渐降低耦合（增加g )，相位φ 不变，γ 2 逐渐减小而 γ 图 1 的变化略有变化，如图 4b、c 所示。耦合参数κ 超过暗模式γ的阻尼常数 2为最小间隙距离，这证实了从明模式到暗模式的耦合强于石墨烯片中的耗散过程。

<图片>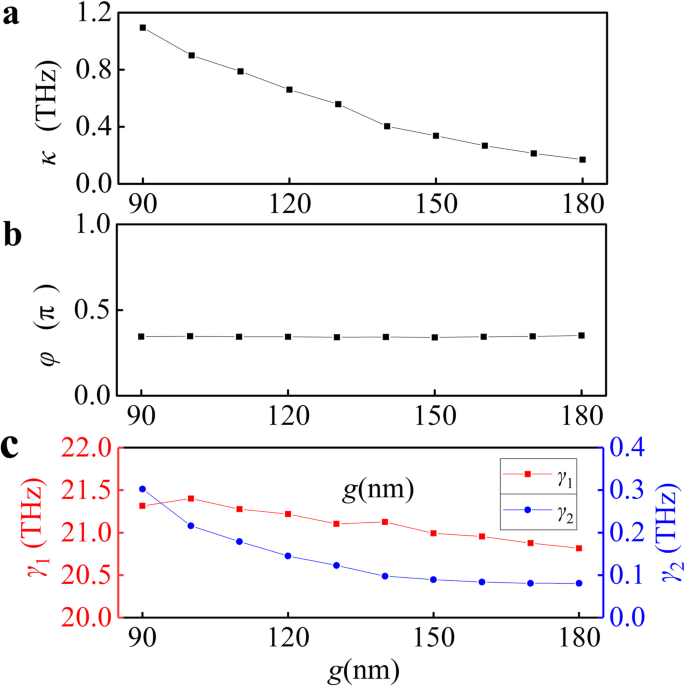

耦合系统中光学响应的​​定量分析。提取的数字 (a ) 耦合, (b ) 阶段，和 (c ) 作为间隙函数的阻尼系数 g . κ 的值 , φ , 和 γ 1、γ 2通过拟合数值吸收光谱提取

为了可视化明暗模式之间的相长干涉，我们研究了结构随时间的磁场演化，以及两个 H z 监视器分别放置在距石墨烯中心 3 nm 和距银槽底部 1000 nm 的位置。两种模式之间的振荡相位差为 0.5π，如图 5a 所示。在PIA共振频率f中计算了不同时间的磁场分布 q =32.5 THz，其中 ω qt 1 ~ 2.00 π 和 ω qt 2 ~ 2.50π，如图 5b、c 所示。可以在 2.00π 处观察到银槽中的磁场最大值，而石墨烯中的磁场在 2.50π 处达到最大值，表明两种结构之间存在异相耦合。因此，共振的演化和形成是由相长干涉决定的[39]。

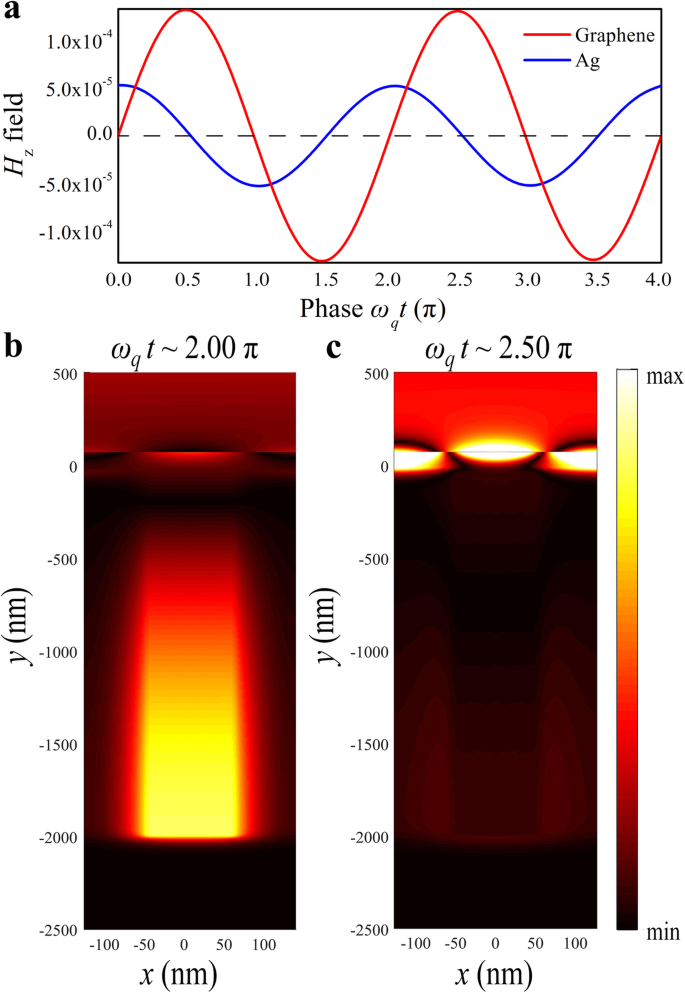
耦合模式的时域演化。 一 计算出石墨烯（红线）和银槽（蓝线）处磁场强度的时间演变。计算的 z g 的磁场分布分量 =90 纳米。在不同时间观察到银槽和石墨烯的最大场强b ω qt 1 ~ 2.00π 和 c ω qt 分别为2～2.50π

在实际应用中，非常需要窄的反射带和高的消光比。为了达到这两个条件，我们可以调整单位P的周期 和银槽深度d 优化我们的结构参数。计算不同结构参数的反射光谱后P 从 1900 到 2100 nm 和 d 通过 FDTD 从 245 到 265 nm，我们在 P 中获得了非常高的消光比 ~ 99.999% =254 nm 和 d =1980 纳米。 PIA 器件在不同折射率环境下的反射光谱如图 6a 所示。感知能力定义为[39]：

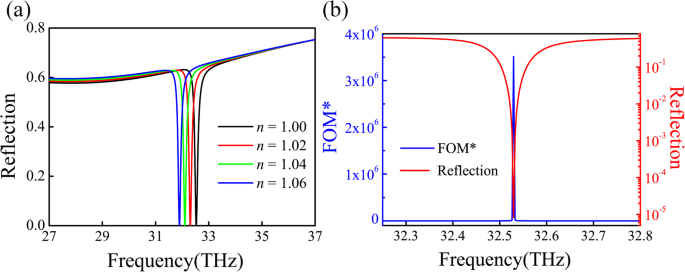
系统的传感性能。 一 PIA 传感器对不同介电环境的感测响应。 b 相关FOM*曲线及反射光谱

其中 f 和我 分别是共振频率和光谱强度。在测量传感器的反射强度时，可以通过 FOM* 值来量化传感器的灵敏度能力。该值越高意味着传感器的灵敏度越高。从图 6a 中，我们可以得到 S =11.2 THz/RIU 和相关的 FOM~94.1，半高全宽 (FWHM) ~ 30 nm (0.12 THz)。该 FOM 大于基于表面晶格共振的超材料吸收器中的值。此外，我们的 PIA 传感器可以导致超高 FOM* 值 3.5 × 10 ⁶ ，如图 6b 所示。我们在附加文件 1：表 S1 中比较了最近研究的传感器的性能。

在 PIA 系统中，石墨烯扮演着另一个关键角色。谐振频率的调制可以通过调节栅极电压来调节石墨烯的费米能级来实现。模拟光谱显示在附加文件 2：图 S1 和 3：图 S2 中。 PIA谐振的频移主动控制对于传感器或吸收器具有重要意义。

结论

总之，我们已经在数值上证明了由 F-P 共振模式和石墨烯等离子体准导模式之间的相长干涉引起的完美吸收。通过引入石墨烯等离子体准导模，我们获得了银槽F-P共振模线宽更窄的谱线。当距离 g 逐渐增加，谐振强度和线宽将减小。对于应用，我们系统中的FOM*可以达到10 ⁶ .此外，可以通过改变几何参数和石墨烯费米能级来调整吸收窗口。这些结果为实现纳米级中红外动态光谱控制和超灵敏光学传感器提供了一条新途径。

数据和材料的可用性

本研究期间生成或分析的所有数据均包含在这篇已发表的文章 [及其补充信息文件] 中。

缩写

FDTD：

有限差分时域

FOM*：

品质因数*

F-P：

法布里-珀罗

FWHM：

半高全宽

PIA：

等离子诱导吸收

坑：

等离子诱导透明

Q 因素：

品质因数

SSP：

欺骗表面等离子体

TM：

横磁