具有稳定性和电源抑制提升的瞬态增强型稳压器

介绍

在现代纳米级片上系统 (SoC) 设计中，不同的子块通常需要不同的电源轨来实现某些特定功能。此外，整个 SoC 系统可能需要在较宽的输入电压范围内运行，并且仍能提供不受电源条件变化影响的高性能 [1]。因此，采用纳米级技术实现的宽输入电压范围电压调节器 (VR) 可能是此类应用的最合适的候选者之一。与开关稳压器和电荷泵等开关对应物相比，线性 VR 具有精度高、输出噪声低和尺寸紧凑的优势。大多数线性 VR 使用单个电压电源执行其电压调节功能，但只有少数可以实现宽电源范围、低噪声、快速瞬态、高负载能力和额外保护功能的组合 [2,3,4] .

为了实现宽电源范围，必须使用能够承受高压的晶体管。然而，与标准晶体管相比，这种晶体管通常占用更多的面积并且性能更差。减少使用高压晶体管的两种现有解决方案是预调节器方法 [5, 6] 和堆叠低压晶体管方法 [7, 8]。前者使用额外的预稳压器为内核稳压器提供内部电源电压。后者实现了精心设计的堆叠式低压晶体管，以将晶体管的端电压保持在技术限制内 [7]。然而，这些方法限制了电压余量。本文采用自供电技术 (SPT) 来实现较宽的供电范围，这意味着调节回路中的大多数核心模块由所提出的 VR [9] 的调节输出电压供电。无需任何附加电路，通过SPT可以提高VR的性能，同时减少高压器件的数量。

通过使用 SPT，误差放大器 (EA) 的第一增益级由建议的 VR 的稳定输出电压提供。通过精心设计EA的第二级，输入电压的高频噪声对EA的输出电压影响很小。此外，本文采用N型功率晶体管架构。因此，所提出的稳压器具有高电源抑制（PSR）和良好的噪声性能[10,11,12,13,14,15]。

快速瞬态响应也是衡量 VR 性能的重要指标 [16,17,18,19,20]，通常通过添加额外的加速循环来实现 [21]。在本文中，瞬态增强是通过动态负载技术（DLT）实现的。在瞬态响应过程中，DLT 引入了一个随负载情况相应变化的附加电流，作为动态负载，可以抑制稳压输出电压的过冲和下冲[9]。

在 DLT 的帮助下，由于额外的负载电流可以减少非主导极位置的变化，因此在较宽的负载范围内增强了环路稳定性。为了使环路稳定，还使用带有归零电阻的米勒补偿来生成低频极点和额外的零以补偿输出极点。此外，与输出电容串联的电阻引入另一个零来补偿功率晶体管寄生栅极电容产生的极点[6, 9, 22, 23]。

最后，设计了一个嵌入式限流回路，以避免过流损坏并提高所提出的 VR 的可靠性 [9, 24,25,26,27]。

此篇文章的结构如下。 “方法”部分阐述了所提出的 VR 的原理和机制，包括过流保护 (OCP) 电路、DLT 和瞬态增强电路、稳定性提升方法和 PSR 分析。 “结果和讨论”部分显示了性能结果和与其他相关已发表文献的比较。 “结论”部分得出了拟议 VR 的结论。

方法

所提出的 VR 的详细电路如图 1 所示。标准低压 MOS 晶体管、高压晶体管、BJT、N 型耗尽型 LDMOS（横向扩散 MOS）晶体管和二极管被命名为 Mn , HVn , Qn , DNn , 和 Dn ，分别在图中，其中n 是相关设备的序号。

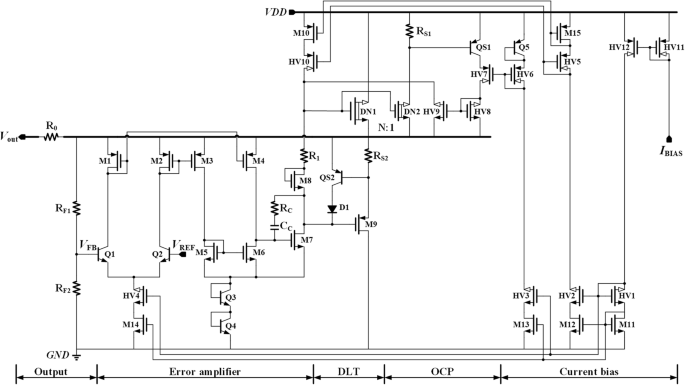
所提出的VR的详细电路

提议的 VR 主要包括五个子模块：电流偏置、OCP、DLT、EA 和输出级。电流偏置电路为整个调节器系统提供偏置电流 [12, 14]。参考电压可以通过多种不同的方式产生[1]，详细电路在此不再展示。嵌入式限流回路用作 OCP 电路，将负载电流限制在预设值。由 DLT 实现的瞬态增强电路通过在瞬态过程中自适应改变负载电流来实现过冲和下冲抑制。 EA和输出功率级形成负反馈调节回路，调节输出电压。假设输出电压V OUT 和反馈电压 V FB 低于期望值时，功率晶体管 DN1 的栅极电压将在调节回路的帮助下上拉以增加输出电压，反之亦然。最后，输出电压可以稳定在

在图 1 中，可以注意到所提出的 VR 的输出电压还为 EA 的第一个增益级（称为 SPT）供电。使用这种电源复用技术，调节回路中的大多数器件都可以由低压器件实现。与高压器件相比，低压器件具有更高的性能、更低的成本和更小的面积，这使得所提出的调节回路更容易实现良好的调节能力。至于EA的第二级，增加了Q3和Q4来提升地电源轨，用于限制M7，VDS_M7的漏源电压。换句话说，Q3和Q4可以防止M7承受过大的电压压力。

为简单起见，后续分析以简化电路来说明创新思路。

提议的 OCP 电路

图 2 显示了建议的 OCP 电路。所提出的限流回路可以根据不同的负载条件自动改变操作模式。当过载发生时，通过降低功率晶体管的栅极电压可以限制所提出的VR的最大电流。

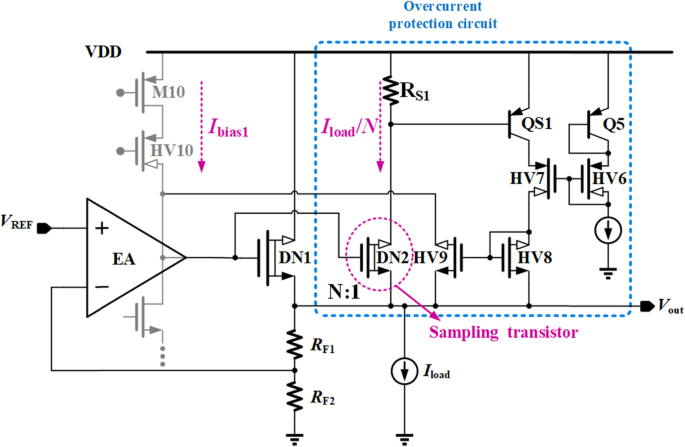
拟定OCP的原则

提出的OCP的机制如下。采样晶体管 DN2 按比例感应流经 DN1 的电流，该电流大约等于负载电流 I 负载，使 R 两端的电压下降 S1，V RS1，反映负载电流水平。一旦V RS1 达到 QS1、HV8 和 HV9 的导通电压将形成一个电流镜以绕过来自 EA 第二级的电流。然后，可以下拉DN1的栅极电压，将负载电流限制在一个预设值，可以表示为

其中 N 是 DN1 与 DN2 的尺寸因子比。 Q5和HV6的目的是为HV7提供适当的偏置电压，从而保护QS1免受过压情况的影响。

在提议的 OCP 中有一个嵌入式负反馈回路。环路增益T 和主导极点p 该电流限制回路的主导性可以由下式给出，

其中 g m_DN2 和 g m_QS1 分别是 DN2 和 QS1 的跨导。 R gate_OC ≈ (g m_HV10r o_HV10r o_M10) || r o_M7 || r o_HV9 和 C 门≈ C gs_DN1 分别为过流时功率晶体管 DN1 栅极节点的等效输出电阻和电容。当建议的 VR 在没有过流的情况下正常运行时，HV9 处于截止区域，因此，DN1 栅极节点的等效输出电阻为 R 门可以表示为 [(g m_HV10r o_HV10r o_M10) || r o_M7]。

提议的 DLT 和瞬态增强电路

图 3 显示了使用 DLT 的瞬态增强电路。由于负载电流与Vgs_DN1成正比，与Vsg_M9成反比，因此流经M9的电流在轻载时较大，在重载时接近于零。因此，随着负载电流的增加，可以将减少的电流引入总输出负载。通过这种方法，可以将该电路均衡为一个动态负载，有助于调节回路的瞬态增强和稳定性提升。

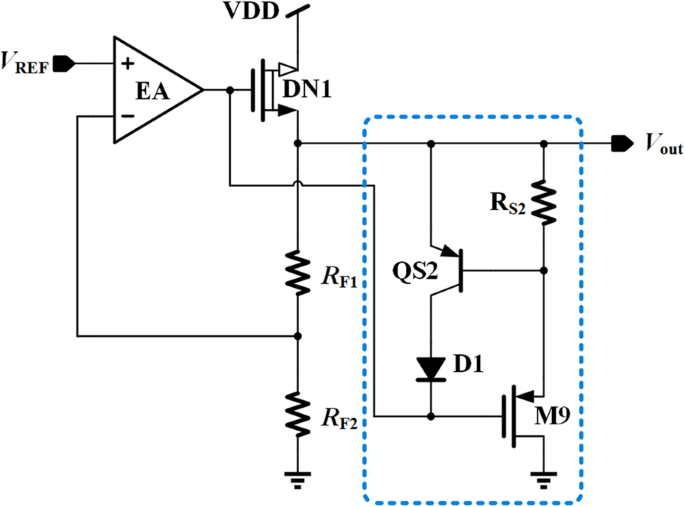
提出的瞬态增强电路

详细的瞬态增强工作原理如下。如果负载电流突然下降，由于环路调节能力和压摆率有限，流经功率晶体管DN1的电流不会立即改变。该电流（在图 4a 中显示为黄色路径）将导致输出电压过冲，从而增加 R 上的电压降 S2和M9。然后一个额外的电流流过 R S2 和 M9（在图 4a 中显示为蓝色路径）在稳压输出处生成，以抵消不需要的黄色路径电流。因此，有效降低了输出电压尖峰。

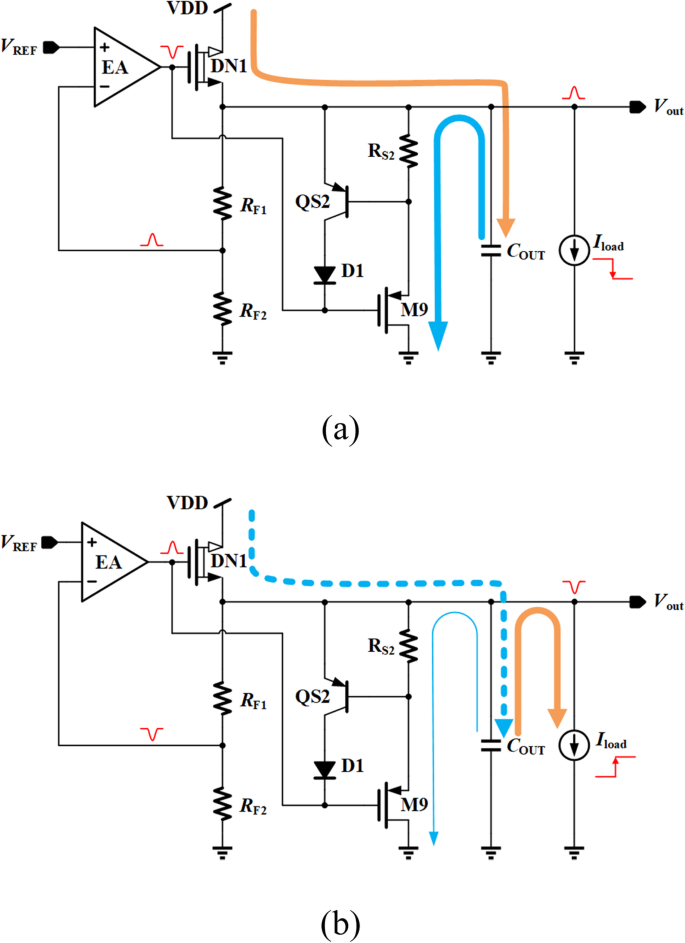
提议的 VR 的瞬态响应。 一 重载到轻载电流变化。 b 轻重负载电流变化

图 4b 展示了轻到重负载电流变化的情况，其中稳压输出出现下冲，然后流过 R 的电流 S2和M9减小。这相当于提供了一个减小的电流负载，从而增加了流经功率晶体管DN1的净电流，从而达到了抑制下冲电压的目的。

为了防止 M9 过流，增加了 QS2 和 D1。当 R 两端的电压 S2 大于 QS2 的开启电压，额外的电流将流入 QS2 和 D1。 M9中的最大电流设置为

D1的作用是防止QS2掉入反向放大区，并在其中流过反向电流，这是M9限流功能的异常状态。

建议 VR 的稳定性提升

如图5所示，存在三个极点ω p1，ω p2 和 ω p3 和两个零 ω z1 和 ω z2 在控制回路中，所提出的 VR 的回路增益为

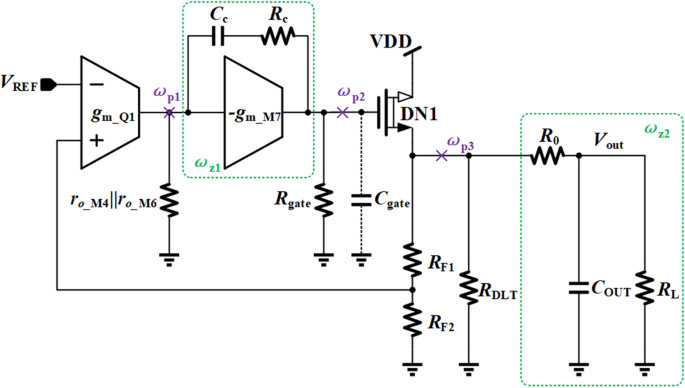
提出的 VR 的极点和零点分布

其中 A O 是 VR 的开环增益，β 是反馈系数，

$$ {A}_O={A}_{\mathrm{CD}0}{A}_{E0}\frac{\left(1+s/{\omega}_{Z1}\right)\left( 1+s/{\omega}_{Z2}\right)}{\left(1+s/{\omega}_{P1}\right)\left(1+s/{\omega}_{P3} \right)\left(1+s/{\omega}_{P2}\right)} $$ (7) $$ \beta =\frac{R_{\mathrm{F}2}}{R_{\mathrm {F}1}+{R}_{\mathrm{F}2}} $$ (8)

其中 A CD0 ≈ 1 是作为电压跟随器工作的功率级的低频增益，A E0 为 EA 的低频增益，

$$ {A}_{E0}={g}_{m\_Q1}\left({r}_{o\_M4}\Big\Vert {r}_{o\_M6}\right){g} _{m\_M7}{R}_{\mathrm{gate}} $$ (9)

考虑到 DN1 栅极节点处的米勒效应和寄生电容，极点和零点写为 [13]

$$ {\omega}_{p1}=1/\left[{g}_{m\_M7}{R}_{\mathrm{gate}}{C}_c\times \left({r}_{ o\_M4}\Big\Vert {r}_{o\_M6}\right)\right] $$ (10) $$ {\omega}_{p2}={g}_{m\_M7}/{ C}_{\mathrm{gate}} $$ (11) $$ {\omega}_{p3}=1/\left\{\left[{R}_L\Big\Vert \left({g}_ {m\_\mathrm{DN}1}^{-1}\Big\Vert {R}_{\mathrm{DLT}}+{R}_0\right)\right]{C}_{\mathrm{ OUT}}\right\} $$ (12) $$ {\omega}_{z1}=1/\left[{C}_c\left({R}_c-1/{g}_{m\_M7 }\right)\right] $$ (13) $$ {\omega}_{z2}=1/\left[\left({R}_0\Big\Vert {R}_L\right){C}_ {\mathrm{OUT}}\right] $$ (14)

其中 R DLT为瞬态增强电路等效电阻； C OUT 为建议 VR 的输出电容。

由于补偿电容C C 被放大 (g m_M7R 门）由于节点 p1 处的米勒效应，极点 ω p1 是主导极点。第二个极点应该是ω p3，因为C OUT 通常在几个微法拉的范围内。虽然寄生电容 C 门相对较大，但仍小于节点 p1 处的等效电容和输出电容。此外，节点 p2 处的电阻仅为 1/g m_M7。因此，极点ω p2 位于高频。零 ω z1是消除中频极点ω p3.电阻R 0 生成零 ω z2 补偿内部寄生极点ω p2。所提出的 VR 的稳定性可以通过电阻 R 来提高 0 增加。然而，电阻R 0 会因负载电流引起的压降而增加输出电压的误差。因此，电阻R 0 应设置在一个合理的值，以在输出电压精度和环路稳定性之间取得良好的平衡。

在没有 DLT 的传统稳压器中，由于负载电流变化引起的功率晶体管跨导变化，输出节点的极点将处于不同的频率。随着负载电流的增加，功率晶体管的跨导g 米 _DN1 会增加，因此输出极点将向高频移动，而其他零点和极点保持在同一位置，如图 6a 所示。这可能会使系统的频率补偿更加困难，并且会减慢轻负载条件下的瞬态响应。更严重的是，系统可能不稳定。

<图片>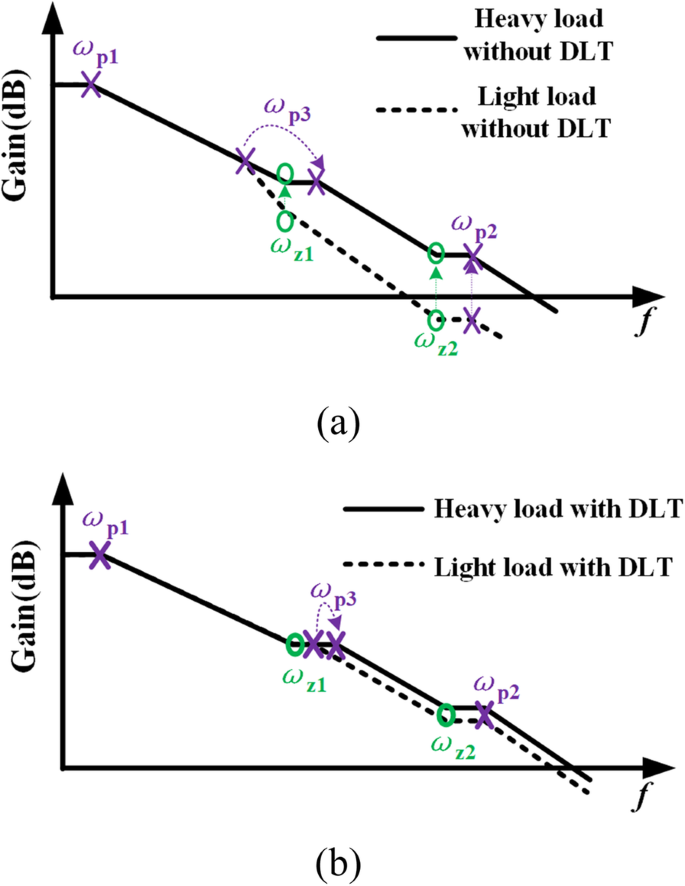

电压调节器的频率响应。 一 无动态负载技术的电压调节器。 b 所提出的具有动态负载技术的电压调节器

在所提出的 DLT 的帮助下，所提出的 VR 在不同负载下具有更好的稳定性。如前所述，通过动态负载电路的电流随着负载电流在稳态下增加而减少，反之亦然。由于该电流由 DN1 提供，因此可以在更宽的负载电流范围内抑制 DN1 的跨导变化，这有助于通过使用建议的 DLT 在更宽的负载范围内实现系统稳定性和带宽恒定。所提出的VR的频率响应如图6b所示，可以保证快速瞬态响应的稳定性。

输出电容设置零位ω z2.通过合理放置零极点，系统在不同的C下会有更好的稳定性 出来了。

拟议 VR 的 PSR 分析

PSR是衡量稳压器性能的关键参数之一，它是指对电源电压产生的高频纹波和噪声的抑制能力。本节采用Gupta 12提出的PSR分析方法，其主要思想是将整个稳压系统简化为分压器模型。如图 7 所示，有两条来自 V 的噪声路径 dd 到 V 输出：路径 1 将噪声从功率晶体管 DN1 的漏极直接传输到 V 出去;路径2是从EA的第二级到功率晶体管DN1的栅极。路径2的效果可以表示为

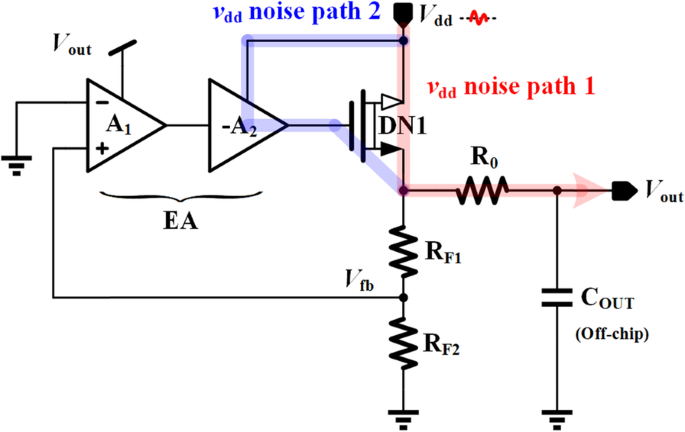
拟议VR的PSR分析

如（15）所示，A 在提议的 SPT 和共源共栅电流镜结构的帮助下，path2 非常小。这使得路径1的影响在PSR分析中占主导地位。

所提出的 VR 的简化 PSR 模型如图 8 所示，其中 r o_DN1 为功率晶体管 DN1 的输出电阻，占噪声通路 1，受控电流源源自噪声通路 2，Z B 由 R 组成 F1，R F2，R 0 和 C OUT 作为高频滤波器，Z SH_FB 是包含负反馈回路功能的等效阻抗。 Z SH_FB 可以由

给出 $$ {Z}_{SH\_ FB}=\frac{1}{g_{m\_ DN1}\left(1+\beta {A}_E\right)} $$ (16) <图片>

PSR的简化模型

其中 g m_DN1 是功率晶体管 DN1 的跨导。因此，PSR 传递函数可以表示为

通过故意设置 HV10 的固有增益远大于功率晶体管 DN1，g m_DN1r o_DN1A 可以实现path2 <<1，因此可以忽略受控电流源。 PSR的表达式可以进一步简化为

由于 Z B 和 Z SH_FB会随着频率的变化而变化，需要分析PSR的频率特性。

低频

在低频时，EA 的增益非常高，C OUT 可被视为开路。因此，Z B>> Z SH_FB 和 PSR 可以写成

中频

Z 的阻抗 SH_FB 将增加，因为环路增益在中频下降。在这个阶段，Z SH_FB还小，PSR主要受环路增益影响。对于(7)，PSR可以表示为

如式(20)所示，在单位增益频率范围内，随着频率的增加，PSR越来越差，输出电压噪声更严重。

高频

由于频率的增加，Z SH_FB 变大，最终接近 1/g m_DN1。 C 的阻抗 OUT变小了，但仍然比R大很多 0. 所以 R 0 可以像以前一样省略。高频 PSR 取决于 r 之间的分压 o_DN1 和 1/g m_DN1 与 C 并联 OUT，可以表示为

在高频时，由于C的作用，可以大大抑制输出电压处的噪声 出来了。

如前所述，所提出的 VR 在全频率范围内的良好抗噪能力由三个方面来保证。首先，采用高环路增益；其次，SPT使电源噪声对功率晶体管的栅极影响很小；三、输出电容C OUT可以提高高频的PSR，并具有滤波特性。

结果与讨论

提议的 VR 已在标准 0.35-μm BCD 技术中实施。制作的稳压器的芯片照片如图9所示，VR的有源核心面积为290 μm×900 μm。

提议的VR芯片照片

建议 VR 的稳压输出电压为 5 V，电源电压范围为 5.5 至 30 V，输出电容为低成本陶瓷电容。输出电容的容量可设置为100 nF至3.3 μF。

图 10 展示了建议 VR 在不同负载条件下的频率响应，输出电容为 100 nF 和 3.3 μF。所提出的LDO可以在很宽的输出电容值范围内保持稳定，并且环路频率响应的波形在0和30 mA负载电流之间的差异很小，这得益于之前分析的所提出的DLT。

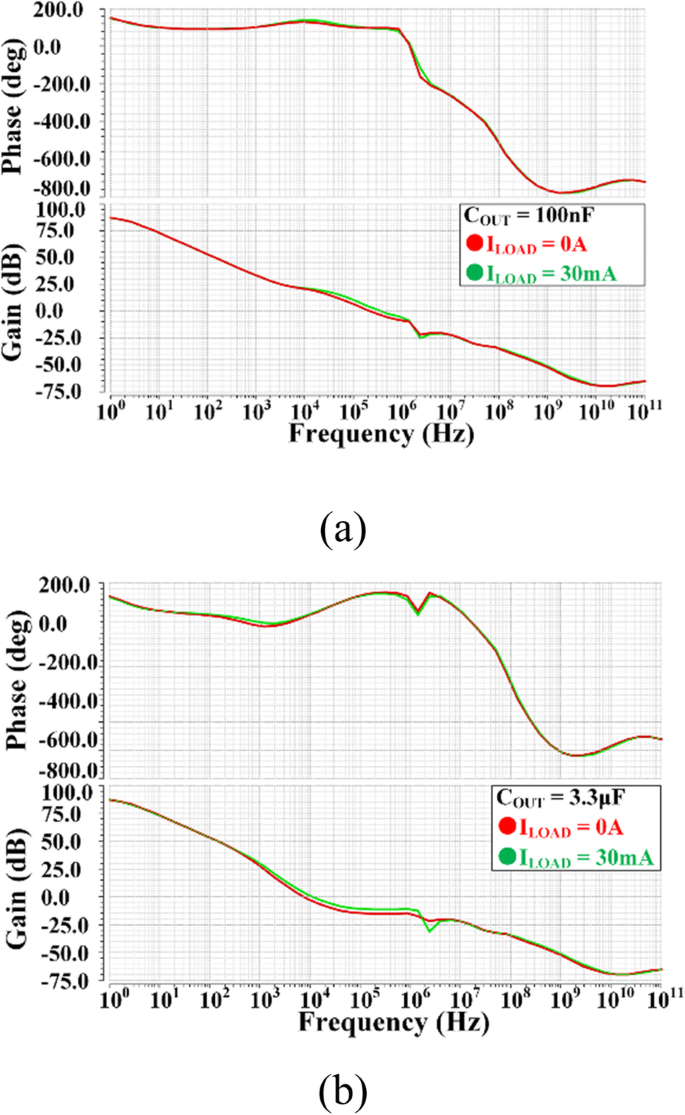
不同I值下提出的VR的环路频率响应 加载和C OUT 条件。 一 COUT =100 nF，b COUT =3.3 훍F。红绿线代表I 负载分别为0 A和30 mA

使用 0.1 μF 输出电容器的 PSR 验证结果如图 11 所示，其中在低频时为 - 110 dB，在高达 10 MHz 时优于 - 64 dB。在低频下，由于高环路增益，建议的 VR 具有良好的 PSR。由于主导极点 ω，PSR 在单位增益频率内变差 p.输出电容C OUT 改善了高频下的 PSR 特性。这些结果表明它与之前的分析是一致的，并且所提出的 VR 在全频范围内获得了更好的 PSR。

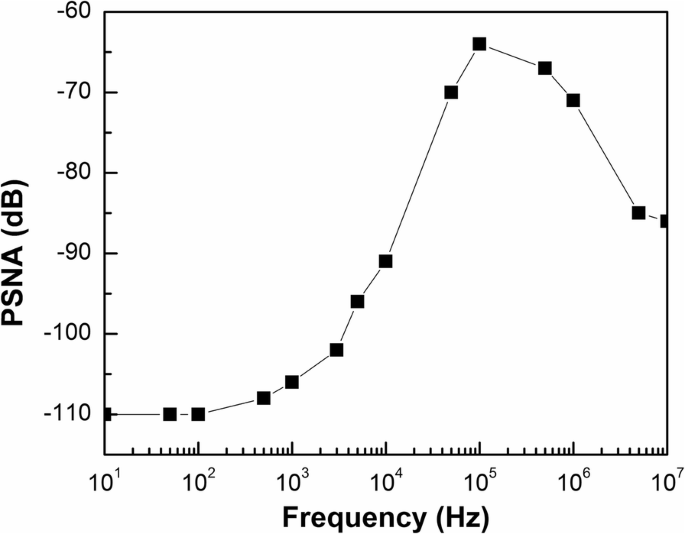
提议的VR的PSR

提出的 VR 的线路调节结果如图 12 所示。在 5.5 至 30 V 的输入电压范围内，输出电压仅变化 73.53 μV，这导致线路调节仅为 2.98 μV/V。这证实了提议的 SPT 的有效性。

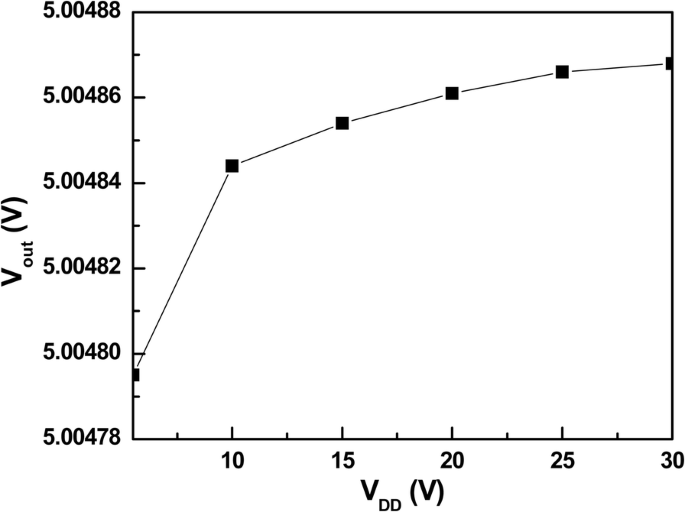
拟VR线规

图 13 显示了不同负载电流对输出电压的瞬态响应。当负载电流从0变为18 mA、28 mA和32 mA时，稳压输出电压的电压尖峰和下降分别约为43 mV、65 mV、83 mV。这导致负载调整率为 0.233 mV/mA​​，这主要是由 R 引起的 0 稳定，输出电容范围宽。

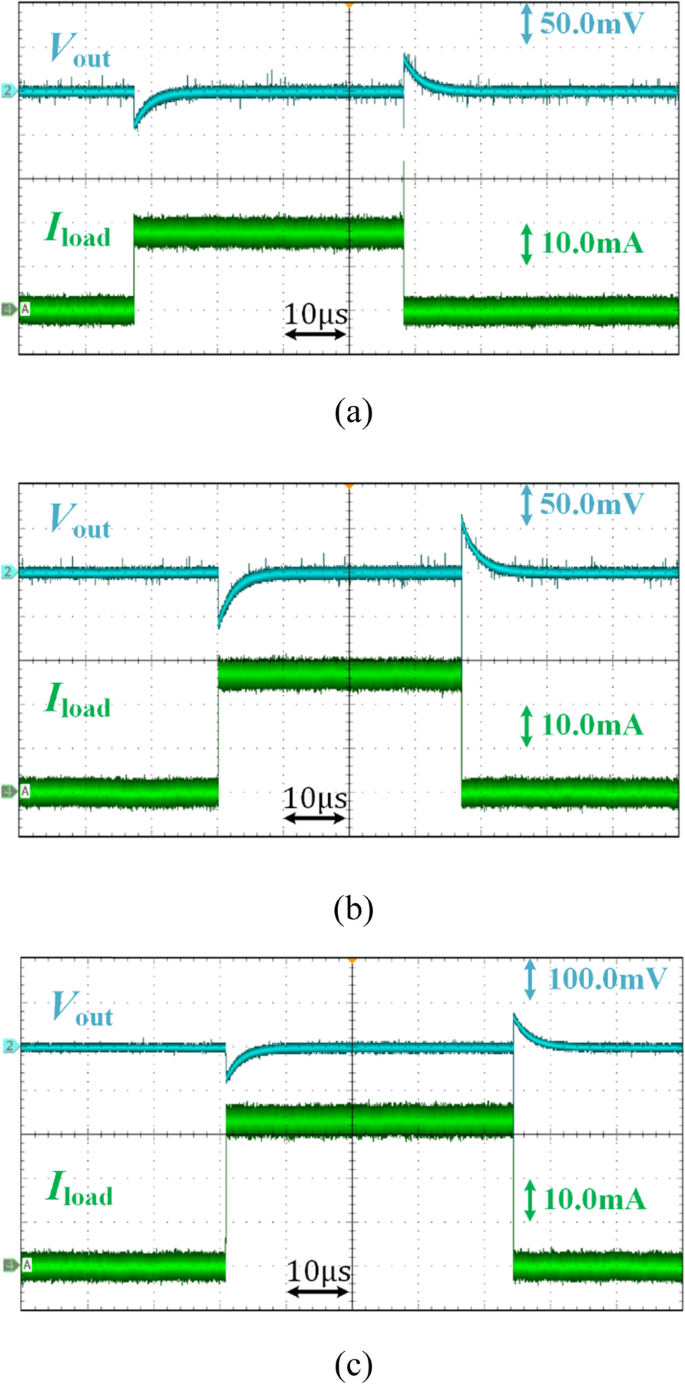
由于不同的负载电流阶跃，建议的 VR 的瞬态响应波形。 一 0～18 mA； b 0～28 mA； c 0～32 mA

测得的OCP如图14所示。为了验证OCP的有效性，图14a采用短路。如图 14a 所示，当输出电压被拉到地时出现过电流，建议 VR 的输出电流保持在 40 mA 左右。图 14b 显示了过流和正常负载之间的瞬态响应，表明所提出的 VR 具有过载退出时的自恢复能力。

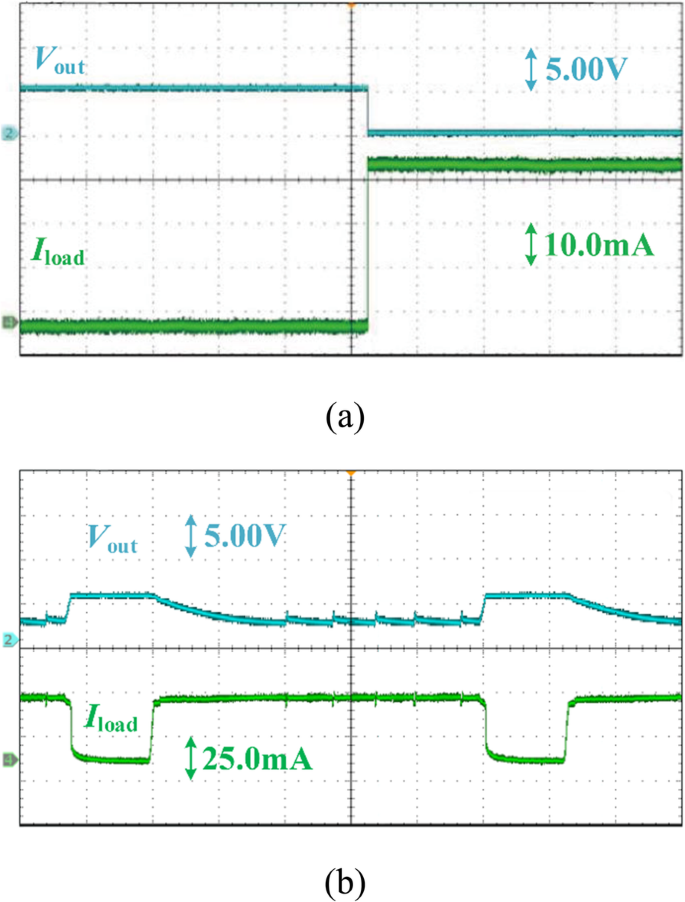
提议的 VR 的 OCP 测量。 一 输出短路； b 过流和正常负载之间的瞬态

表 1 提供了建议的 LDO 和一些其他先前发布的 LDO 的性能比较。相比之下，该 LDO 具有最佳的线路调节和 PSR，这得益于所提议的 SPT。如果采用更先进的工艺制造，活性面积将进一步缩小。

表 2 提供了另一个性能比较，重点是同样具有宽电源范围的 LDO。在提议的 DLT 和 SPT 的帮助下，与其他 LDO 相比，这项工作具有最佳的线路调节和最宽的电源范围。附加的 OCP 功能使这项工作更具竞争力和可靠性。

结论

具有 DLT 和 OCP 的高稳定性 SPT VR 在标准 0.35-μm BCD 工艺中实现。在 SPT 的帮助下，大部分调节回路由调节后的输出电压提供，这有利于稳定性和 PSR 的提高。提议的 DLT 有助于瞬态响应和稳定性。此外，内嵌的OCP电路可以防止所呈现的VR因过载或短路而损坏。建议的 VR 的线性调节率为 2.98 μV/V，VDD 为 5.5 至 30 V，而调节后的输出电压为 5 V，负载调节率为 0.233 mV/mA​​，负载电流为 0A 至 30 mA。通过使用所提出的瞬态增强电路，负载电流变化期间的过冲和下冲电压也很小。低频下的 PSR 为 − 110 dB，并且优于 − 64 dB 直至 10 MHz。可以在较宽的输出电容和负载电流范围内实现高环路稳定性，因此所提出的VR适用于在输出电容和负载电流变化下需要高性能和可靠性的应用。

数据和材料的可用性

本研究期间生成或分析的所有数据均包含在这篇已发表的文章中。

缩写

VR：

稳压器

OCP：

过流保护

SPT：

自力技术

PSR：

电源抑制

分布式账本技术：

动态加载技术

EA：

误差放大器