电容器和微积分

电容器不像导体那样具有稳定的“电阻”。但是，电容器的电压和电流之间存在明确的数学关系，如下所示：

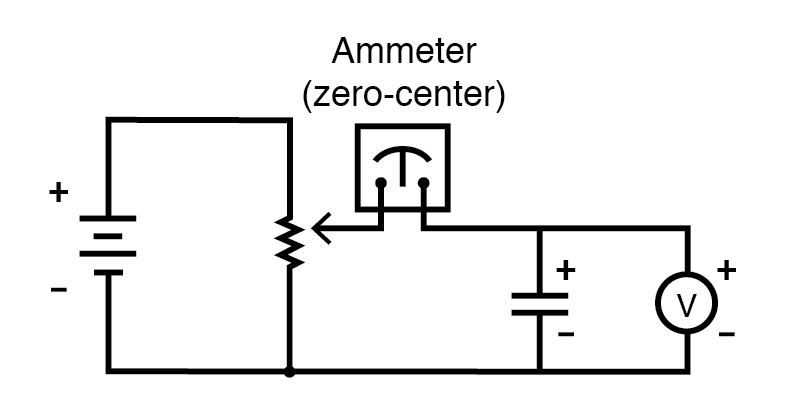
小写字母“i”象征瞬时 电流，表示特定时间点的电流量。这与未指定时间段内的恒定电流或平均电流（大写字母“I”）形成对比。 “dv/dt”这个表达是从微积分中借来的，意思是电压随时间的瞬时变化率，或电压在特定时间点的变化率（伏特每秒增加或减少），同一特定点在参考瞬时电流的时间。无论出于何种原因，字母 v 通常用来表示瞬时电压而不是字母e .但是，将瞬时电压变化率表示为“de/dt”并没有错。

在这个等式中，我们看到了迄今为​​止我们在电路方面的经验中的一些新事物：时间变量 .当将电压、电流和电阻的量与电阻相关联时，我们处理在未指定时间段 (E=IR；V=IR) 或特定时刻进行的测量并不重要时间（e=ir；v=ir）。同样的基本公式也成立，因为时间与电阻器等元件中的电压、电流和电阻无关。

然而，在电容器中，时间是一个基本变量，因为电流与快速有关 电压随时间变化。为了完全理解这一点，可能需要一些插图。假设我们要将一个电容器连接到一个由电位计和电池构成的可变电压源：

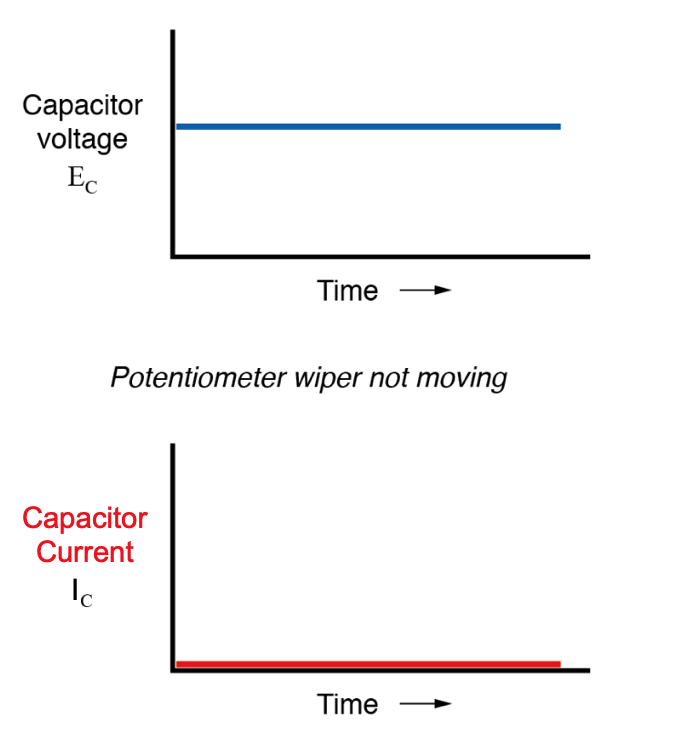
如果电位计机构保持在单个位置（雨刷器静止），则连接在电容器两端的电压表将记录一个恒定（不变）电压，而电流表将记录为 0 安培。在这种情况下，电压的瞬时变化率 (dv/dt) 为零，因为电压是不变的。该方程告诉我们，对于 dv/dt，每秒变化为 0 伏，瞬时电流 (i) 必须为零。从物理的角度来看，在电压不变的情况下，不需要任何电子运动来增加或减少电容器极板上的电荷，因此不会有电流。

现在，如果电位计游标在“向上”方向缓慢而稳定地移动，电容器两端将逐渐施加更大的电压。因此，电压表指示将以缓慢的速度增加：

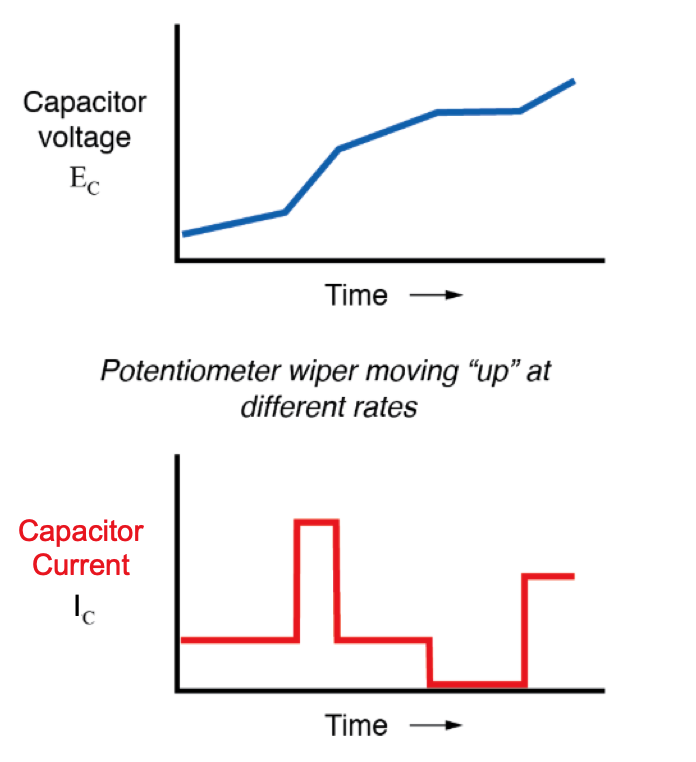
如果我们假设正在移动电位计游标使得 rate 如果电容器两端的电压增加稳定（例如，电压以每秒 2 伏的恒定速率增加），则公式的 dv/dt 项将是一个固定值。根据等式，dv/dt 的这个固定值乘以电容器的电容法拉（也是固定的），得到一定量级的固定电流。从物理角度来看，电容器两端电压的增加要求极板之间的电荷差增加。因此，对于缓慢、稳定的电压增加速率，电容器中必须有缓慢、稳定的电荷建立速率，这相当于缓慢、稳定的电流流动。在这种情况下，电容器正在充电并充当负载 ，随着电容器在电场中积累能量，电流进入正极板并从负极板流出。

如果电位器向同一方向移动，但速度更快，电压变化率 (dv/dt) 会更大，电容器的电流也会更大：

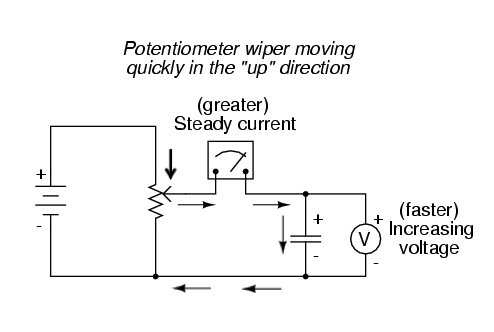
当数学学生第一次学习微积分时，他们首先探索变化率的概念 用于各种数学函数。 导数 是第一个也是最基本的微积分原理，它是一个变量相对于另一个变量的变化率的表达式。微积分的学生必须在学习抽象方程的同时学习这个原理。你可以在学习与你相关的东西的同时学习这个原理：电路！

用微积分来表示电容器中电压和电流之间的这种关系，通过电容器的电流是导数 电容器两端的电压与时间的关系。或者，简单地说，电容器的电流与其两端电压的变化速度成正比。在这个通过电位器旋钮位置设置电容电压的电路中，我们可以说电容的电流与我们转动旋钮的速度成正比。

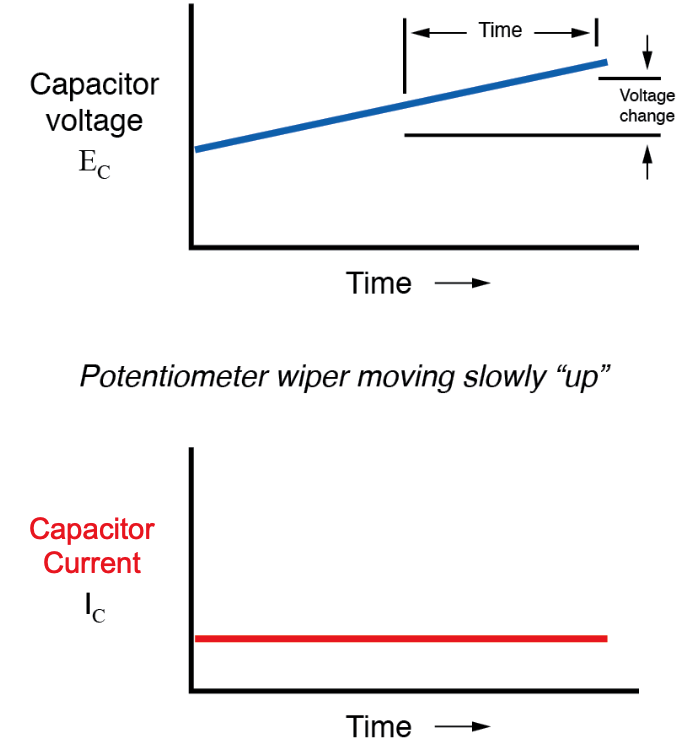
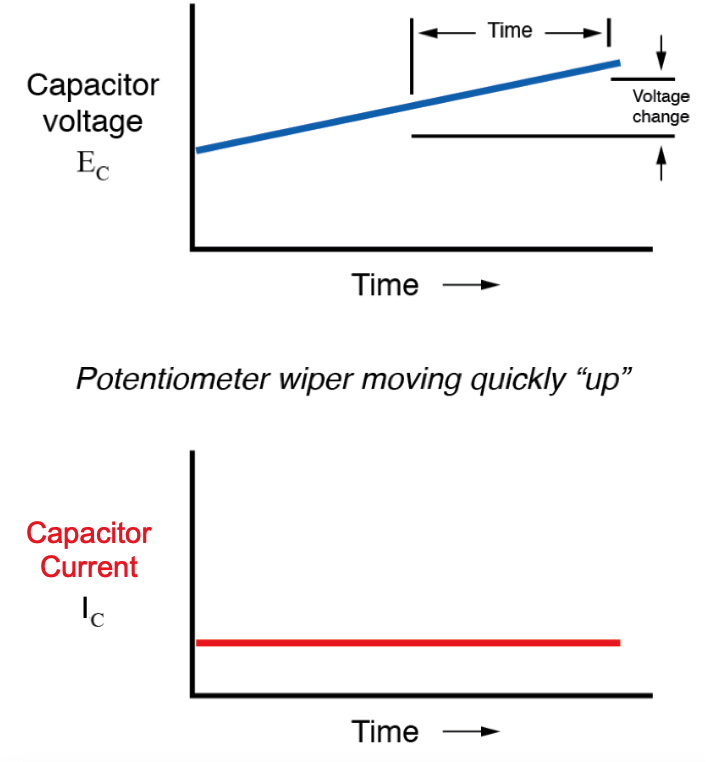
如果我们沿与之前相同的方向（“向上”）移动电位计的游标，但以不同的速率移动，我们将获得如下图：

请注意，在任何给定的时间点，电容器的电流都与变化率或斜率成正比 , 电容器的电压图。当电压曲线快速上升（陡坡）时，电流同样会很大。在电压曲线有轻微斜率的地方，电流很小。在电压图中的某个位置趋于平稳（零斜率，代表电位器未移动的一段时间），电流降至零。

如果我们在“向下”方向移动电位器游标，电容电压会降低 而不是增加。同样，电容器将通过产生电流对这种电压变化作出反应，但这次电流将在相反的方向上。降低电容器电压需要减小电容器板之间的电荷差异，唯一可能发生的方法是电流方向相反，电容器放电而不是充电。在这种放电条件下，电流从正极板进入负极板，电容器将充当源 ，就像电池一样，将其储存的能量释放到电路的其余部分。

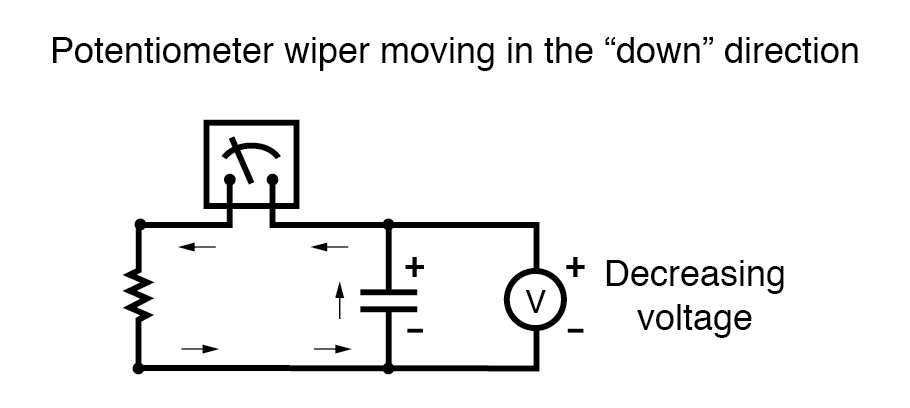
同样，通过电容器的电流量与其两端的电压变化率成正比。 减少的影响之间的唯一区别 电压和增加 电压是方向 的电流。对于相同的电压随时间变化率，无论是增加还是减少，电流幅度（安培）都将相同。在数学上，降低的电压变化率表示为负 dv/dt 数量。遵循公式 i =C(dv/dt)，这将导致电流值 (i) 的符号同样为负，表示对应于电容器放电的流动方向。

相关工作表：

• 电容器工作表
• 电路微积分工作表