使用单个 MoS2 光栅的双轴应变传感器

介绍

柔性电子技术受到学术界和工业界的广泛关注，但由于动态位移和变形监测的困难，微尺度和纳米尺度柔性器件的设计和应用具有挑战性[1,2,3,4,5]。大多数基于电阻应变片的传统应变检测方法需要微型传感器阵列 [4, 6, 7]，这对于柔性电子应用来说很难生产。基于光学的二维 (2D) 应变检测技术，例如散斑干涉法，由于精度更高，因此优于基于压阻的技术 [8]。然而，他们的图像相关性测量策略受到复杂图像处理技术要求的挑战[8,9,10]。反射光栅可以为应变测量提供高分辨率，但缺乏在单个器件内检测二维应变的能力[11]。

在过去的几年里，二维材料吸引了大量的研究工作。随着石墨烯 [12, 13] 的引入，二维材料家族又增加了许多新成员，如双原子薄黑磷 [14]、三原子薄过渡金属二硫属化物 [15]、四原子薄族 III金属单硫属化物 [16] 和其他非层状 2D 材料 [17]。在这些材料中发现了许多有趣的特性，使它们成为材料科学的焦点[18,19,20,21,22,23,24]。

过渡金属二硫属化物表现出出色的光学和机械性能 [25,26,27]。例如，MoS2 可以承受高达 19.5% [26] 的双轴应变及其反射调制 [28]，并且 WSe2 可以通过应变工程显示出显着的 Berry 曲率偶极子和非线性霍尔效应 [29]。将材料反射光谱的应变敏感性结合到反射光栅装置的功能中，可以有效地将应变测量扩展到单个装置内的双轴检测。然而，目前还没有将反射光栅与应变诱导材料反射调制相结合用于二维应变传感应用的报道。

在这里，我们提出了一种新型的面内双轴应变传感技术，涉及反射光栅传感器中 MoS2 反射的应变敏感性。第一性原理计算表明，双轴应变可以移动基于 MoS2 的光栅器件衍射图案中强度分布的峰值，因为 MoS2 的反射率对应变引起的变形很敏感。通过在单轴应变线性方程中添加二阶项，可以很好地证明这种非线性峰移，从中可以以 ~ 1‰的精度限制提取垂直于光栅周期方向的应变分量。我们对原型 MoS2 光栅器件的实验研究证实，垂直于光栅周期的应变可以引起光栅一阶衍射图案的强度峰值偏移。我们的研究表明，使用单个光栅传感器可以实现一次性平面内双轴应变仪。

方法

二硫化钼薄片的理论计算

MoS2 对应变的光学响应都是通过使用 Vienna Ab-initio Simulation Package (VASP) [30] 执行的第一性原理计算来研究的。全电子投影仪增强波 (PAW) 电位 [31] 用于所有计算。使用 Perdew-Burke-Ernzerhof (PBE) 广义梯度近似 (GGA) 方法 [32] 进行几何松弛和静态计算。自旋轨道耦合 (SOC) [33] 也包括在静态计算中。为了确定光学特性，首先通过源自格林函数理论的 GW 方法获得准粒子能量 [34]。静态计算得到的波函数和引力波计算得到的准粒子能量被用来进行 Bethe-Salpeter 方程 (BSE) 计算 [35] 来预测介电常数。

块状晶体模型用于表示 MoS2 薄片（大于五层的堆叠之间的光学特性差异可以忽略不计[36]）。在优化计算中，能量截止设置为 400 eV，并使用 15*15*4 的 Monkhorst–Pack k 点集对布里渊区进行采样。首先优化晶格参数，作为稍后计算应变 MoS2 薄片的参考。优化后的晶格参数为a =b =3.18 Å 和 c =13.87 埃。放松几何直到能量收敛到 10 ^–5 EV。采用先前文献 [37] 中的技术，能量截止值为 300 eV 和 k - 点集 6 × 6 × 2 用于光学计算。静态能量收敛到10 ^–6 eV 在所有计算中。衍射图案是基于亥姆霍兹-基尔霍夫定理 [38] 模拟的。附加文件 1 中提供了更多详细信息。

准备用于光谱测量的 MoS2 样品

MoS2 薄膜从商业 MoS2 单晶（SPI Supplies）机械剥离，并用胶带转移到聚二甲基硅氧烷（PDMS）基材上。转移后，在薄片和基材上制作另一层PDMS以增强附着力。

在柔性基板上制备二硫化钼光栅

MoS2 薄膜从商业 MoS2 单晶（SPI Supplies）机械剥离，并用胶带转移到聚二甲基硅氧烷（PDMS）基材上。为了制造光栅器件，首先通过电子束光刻 (EBL) 将 MoS2 薄片图案化成光栅结构。然后用20 W功率的氧等离子体蚀刻图案化的样品。最后，我们通过洗掉PMMA获得了基于MoS2的光栅装置。

MoS2 设备测量

以超连续谱白光源（NKT Photonics SuperK Compact）作为激发激光，通过一个孔径，以相对于样品平面的一定角度撞击薄片样品或光栅样品，如图1所示。在反射率测量中，反射的激光通过连接到光谱仪的光纤收集。不同应变下的反射光谱由光谱仪测得的数据计算得到。为了测试 MoS2 光栅，将反射的激光投射到白板上并显示为长椭圆形光斑。光斑照片用于分析强度分布。

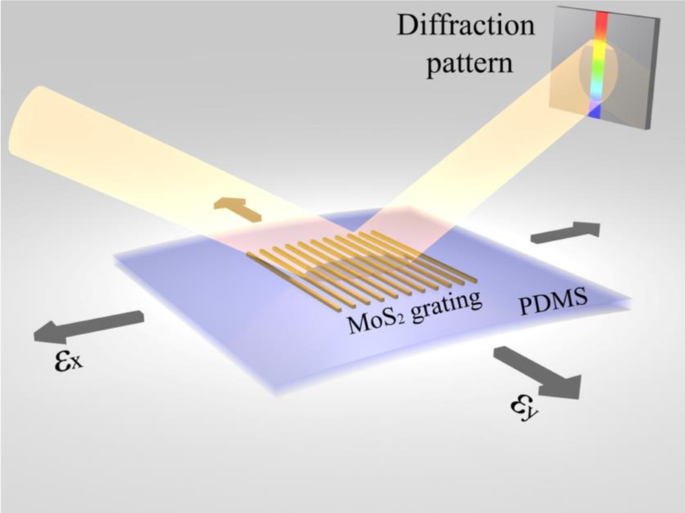
双轴应变片PDMS柔性基板上MoS2基光栅传感器示意图

结果与讨论

在传统的反射光栅传感器中，平行光栅条的周期性结构可以对光进行衍射，通过监测衍射图案的位置偏移，利用衍射来测量沿光栅周期方向的应变[11]。由于周期性结构取向，反射光栅的应变传感功能仅限于面内单轴应变仪（平行于周期性方向）。为了扩展用于面内双轴应变计的反射光栅功能，我们建议光栅材料的固有光学特性，例如材料反射率的应变敏感性，可以被视为一个额外的应变传感器来检测-垂直于周期方向的平面应变分量。

MoS2 具有层状结构：一层 Mo 原子夹在两层 S 原子之间。层之间的相互作用是弱范德华力。在这里，我们设计了一个基于 MoS2 薄片的反射光栅传感器（图 1），并通过第一性原理计算研究了不同面内双轴应变下的器件衍射图案。我们计算中的入射光束波长范围为 400 到 850 纳米。衍射光栅可表示为：

其中\(d\)是两个相邻光栅条之间的距离，\({\theta }_{i}\)是入射光束与光栅法线之间的夹角，\({\theta }_{m }\) 是衍射光束有最大值时衍射光束与法线的夹角，n 是衍射级，\(\λ\) 是光束波长[11]。从方程。 （1），我们看到具有不同 \(\lambda\) 的入射光束必须具有不同的 \({\theta }_{m}\)。因此，连续波长的光束会引起一系列连续的衍射斑对应于不同的\({\theta }_{m}\)，形成椭圆的一阶衍射图。

图 2a 显示了未施加应变时设计的光栅传感器的衍射图案的模拟图像。图 2b 显示了器件在不同双轴应变下模拟的一级衍射图案的强度峰值和图案位置演变。对应于 850 nm 入射光束的一级衍射图案的边缘标记为“LW”。当我们沿光栅周期方向 (\({\varepsilon }_{x}\)) 施加平面内单轴拉伸应变时，该应变会导致间距 d 增加 每个条带之间。结果，\({\theta }_{m}\) 减小，因为\(d\mathrm{sin}{\theta }_{m}\) 对于任何给定的\(\lambda\) 和固定\ ({\theta }_{i}\)。因此，当我们逐渐将应变 \({\varepsilon }_{x}\) 从 0 增加到 4.3% 时，一级衍射图中每个点的位置会向零级衍射斑的中心靠拢与对应的光束波长成正比关系，与传统反射光栅传感器的功能一致[11]。

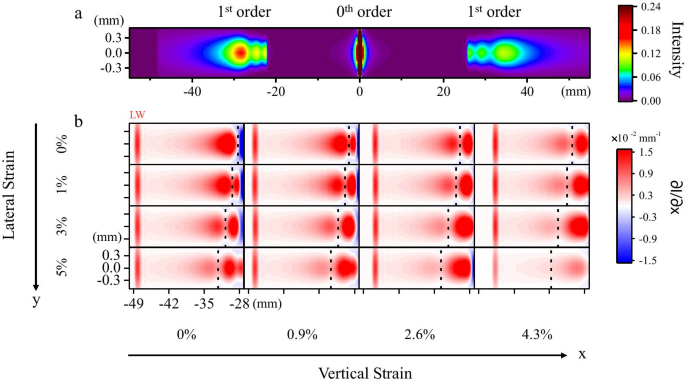
一 衍射图案的模拟图像。没有施加应变。强度用颜色表示。零级光束两侧的一级衍射光斑之间存在不对称行为，因为我们模拟中的屏幕设置为平行于光栅而不是垂直于反射方向。 b 不同双轴应变下一级衍射斑的模拟演化。强度偏微​​分用颜色表示。横坐标和纵坐标表示相对于零级衍射斑中心的位置。峰用虚线标记。从左到右，\({\varepsilon }_{x}\) 分别设置为 0%、0.9%、2.6% 和 4.3%。从上到下，\({\varepsilon }_{y}\) 分别为 0%、1%、3% 和 5%

具有较长波长\(\lambda\) 的入射光束具有较大的\({\theta }_{m}\) 变化，因此LW 边缘具有最明显的位置偏移。然而，当同时施加垂直于光栅周期方向 (\({\varepsilon }_{y}\)) 的面内拉伸应变时，在一级衍射图中观察到强度峰值偏移，如图 2b 中的虚线。当应变 \({\varepsilon }_{y}\) 从 0% 增加到 5% 时，强度峰值进一步远离零级衍射点的中心。我们将强度分布的这种峰移归因于 MoS2 反射率的应变诱导调制。以前的文献报道，MoS2 的反射光谱可以通过外部应变进行调谐 [28]，反射率等于反射光栅的衍射光束与入射光束的强度比。因此，MoS2 光栅衍射的不同波长光束的强度可以通过面内应变进行调制。同时，由于应变\({\varepsilon }_{y}\)对光栅周期没有影响，所以没有发生LW边缘位置偏移。

图 3a 显示了当施加沿 MoS2 的晶格矢量 \({\varvec{b}}\) 的单轴拉伸应变时，MoS2 反射光谱峰值位移的线性行为。这种单轴拉伸应变导致 MoS2 反射率的峰值位置红移。然而，当我们应用面内双轴拉伸应变时，反射峰值位置偏移存在非线性调制。反射光谱峰值位置与面内双轴拉伸应变之间的关系可用二阶方程描述：

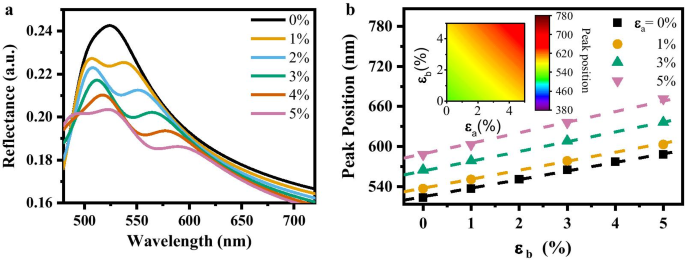
一 在不同单轴应变下，作为波长函数的 MoS2 薄片的反射光谱。 b 不同双轴应变下 MoS2 薄片反射光谱的峰值位置。虚线代表拟合曲线。插图：拟合方程中峰值位置的映射图像

其中 l , m , 和 n 是三个常数，ε 一 和 ε b 是沿 MoS2 的两个晶格矢量的应变分量。第一项描述了沿晶格矢量 \({\varvec{a}}\) 或 \({\varvec{b}}\) 在单轴拉伸应变下峰值位置偏移的线性行为。第二项描述了双轴拉伸应变情况下的高阶行为。第三项是未应变的 MoS2 的反射峰位置。由于 MoS2 晶格向量 \({\varvec{a}}\) 和 \({\varvec{b}}\) 对称等效，因此沿两个方向的拉伸应变具有相同的贡献因子。拟合结果表明，拟合曲线与第一性原理计算峰位的最大差值为1.76 nm，表明利用反射峰位计算可以得到 ~ 1‰的应变仪精度极限应变与方程。 (2).图 3b 显示了从拟合方程获得的不同面内双轴拉伸应变下反射峰位置的映射图像。 (2)（见附加文件1中反射率的详细图）。

在我们的模拟中，晶格向量 \({\varvec{a}}\) 垂直于模拟光栅的周期方向。因此，应变\({\varepsilon }_{y}\) 等于\({\varepsilon }_{a}\)，应变\({\varepsilon }_{x}\) 等于\(\ sqrt{3}/2\times {\varepsilon }_{b}\)。我们的计算表明，在基于 MoS2 的光栅传感器中，面内应变 \({\varepsilon }_{x}\) 可以通过一阶衍射图案的 LW 边缘位置偏移来测量。基于一阶衍射图中的强度峰位移，我们可以利用二阶方程。 (2) 从峰位移中减去面内应变 \({\varepsilon }_{x}\) 的贡献。然后我们可以定量计算面内应变\({\varepsilon }_{y}\).

为了进一步实验研究 MoS2 反射率的应变敏感性，我们机械剥离​​了 MoS2 薄片（厚度为几十纳米；参见附加文件 1 中的详细信息），并通过干燥的方法将薄片附着到聚二甲基硅氧烷 (PDMS) 的柔性基板上。转移方法（如图 4a 插图所示）。通过将基板的两侧固定到两个平移台并拉伸基板，在该制造的 MoS2 器件上施加了面内单轴拉伸应变。我们通过计算 ε 来估计面内单轴拉伸应变 \(=\delta L/L\)，其中\(L\) 是两个夹子之间的基板长度，\(\delta L\) 是长度变化。当应变从 0 到 4% 变化时，MoS2 反射光谱中的峰值位置会发生红移，这种偏移的幅度与我们的理论计算非常吻合，如图 4a 所示。图 4b、c 显示了在通过电子束光刻制造的 PDMS 柔性基板上，周期为 2 μm 的基于 MoS2 的反射光栅传感器的光学图像（方法中的详细信息）。在拉伸 PDMS 基板时，垂直于周期方向的面内拉伸应变施加在基于 MoS2 的光栅器件上（图 4d）。通过监测一级衍射图中的强度分布，我们观察到，当我们引入垂直于 4% 的面内拉伸应变时，与未应变的情况相比，强度峰值移离零级点的中心更远。周期方向（图 4e）。由于拉伸应变垂直于周期方向，因此没有获得衍射图案位置偏移，间距d 每个条带之间变化很小。

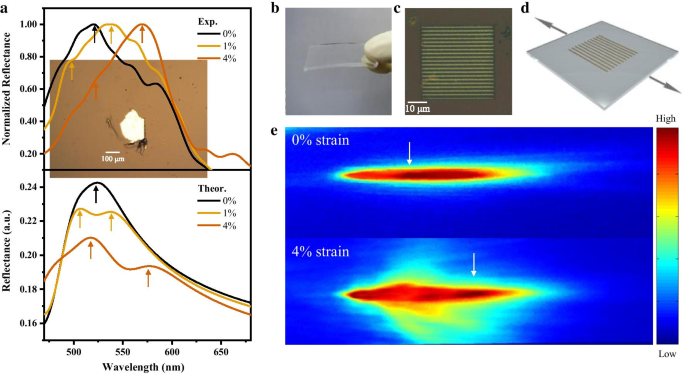
一 单轴应变反射光谱的实验结果（上），第一性原理计算单轴应变的反射光谱（下）。箭头表示反射的峰值位置。插图，用于反射光谱测试的二硫化钼薄片的光学图像。 b –c 在 PDMS 上制作的基于 MoS2 的光栅的光学图像。 d 通过平移阶段拉伸的基于 MoS2 的光栅示意图。 e 未应变（顶部）和应变（底部）光栅的一级衍射点的图像。白色箭头表示强度峰值

结论

总之，我们展示了一种使用基于二硫化钼的反射光栅传感器测量面内双轴应变的新技术。我们通过数值模拟具有高达 5% 的不同双轴应变的光栅来测试这一概念。在这项新技术中，用于检测沿周期方向 (\({\varepsilon }_{x}\)) 的应变分量的光栅结构与 MoS2 反射率的应变敏感性相结合，作为附加传感器，获得垂直于周期方向的面内应变分量 (\({\varepsilon }_{y}\))。分量 \({\varepsilon }_{y}\) 使用二阶近似方程和一阶衍射图案内的强度峰位移计算。我们的实验很好地支持了理论结果。我们的工作为柔性光栅传感器的设计开辟了道路，并提供了一种用单个光栅传感器实现一次性平面双轴应变计的新方法。我们的方法也适用于在双轴应变下具有可预测反射响应和形成二维单晶层能力的其他材料。

数据和材料的可用性

本研究中使用和分析的数据集可向相应作者索取合理要求。

缩写

二维：

二维

VASP：

维也纳从头算模拟包

爪子：

全电子投影增强波

PBE：

Perdew-Burke-Ernzerhof

GGA：

广义梯度逼近

SOC：

自旋轨道耦合

BSE：

Bethe-Salpeter方程

PDMS：

聚二甲基硅氧烷

EBL：

电子束光刻