布尔简化规则
布尔代数在逻辑电路的简化中最实用。
如果我们将逻辑电路的功能转换为符号(布尔)形式,并将某些代数规则应用于所得方程以减少项和/或算术运算的数量,则简化的方程可以转换回电路形式,以便逻辑电路执行相同的功能,更少的组件。
如果可以用更少的元件实现相同的功能,结果将提高可靠性并降低制造成本。
为此,本节介绍了几条布尔代数规则,用于将表达式简化为最简单的形式。
本章已经复习过的恒等式和性质在布尔化简中非常有用,并且在很大程度上与“正规”代数的许多恒等式和性质相似。
但是,本节中显示的规则都是布尔数学所独有的。
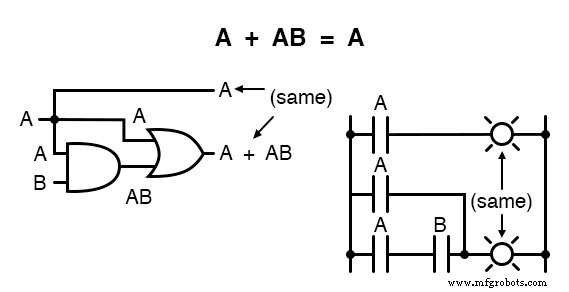
这个规则可以通过从两个项中分解出一个“A”来象征性地证明,然后应用A + 1 =1和1A =A的规则来获得最终结果:
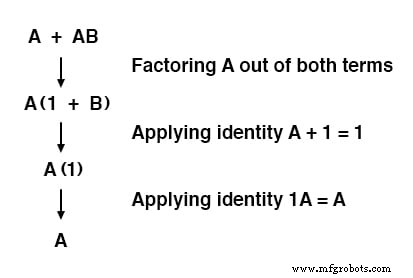
请注意如何使用规则 A + 1 =1 将 (B + 1) 项减少到 1。
当像“A + 1 =1”这样的规则用字母“A”表示时,并不意味着它只适用于包含“A”的表达式。
在像 A + 1 =1 这样的规则中,“A”代表的是任何布尔变量或变量的集合。
这可能是新学生在布尔化简中最难掌握的概念:将标准化的恒等式、性质和规则应用于非标准形式的表达式。
例如,布尔表达式 ABC + 1 也通过“A + 1 =1”恒等式减少到 1。
在这种情况下,我们认识到身份标准形式中的“A”项可以代表原始表达式中的整个“ABC”项。
下一个规则看起来与本节中显示的第一个规则相似,但实际上完全不同,需要更巧妙的证明:
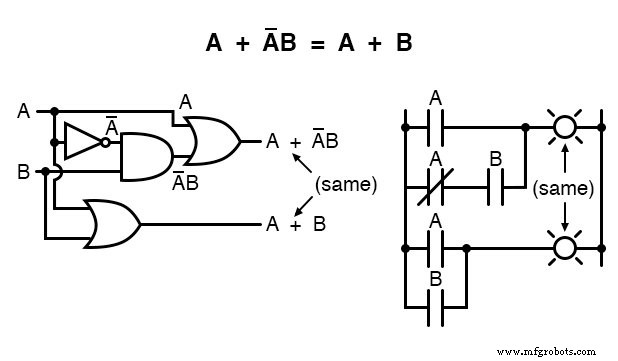
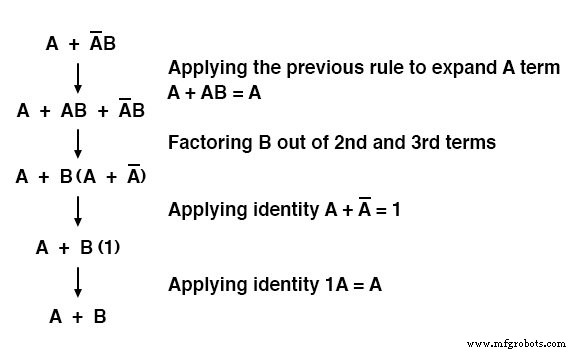
请注意最后一条规则 (A + AB =A) 如何用于“取消简化”表达式中的第一个“A”项,将“A”更改为“A + AB”。
虽然这看起来像是倒退,但它确实有助于将表达式简化为更简单的东西!
有时在数学中,我们必须采取“倒退”步骤来实现最优雅的解决方案。
知道什么时候该走,什么时候不该走是代数艺术形式的一部分,就像国际象棋比赛的胜利几乎总是需要经过计算的牺牲一样。
另一个规则涉及求和表达式的简化:
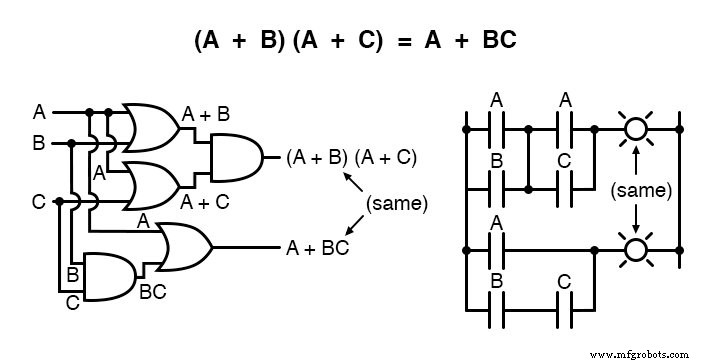
并且,相应的证明:
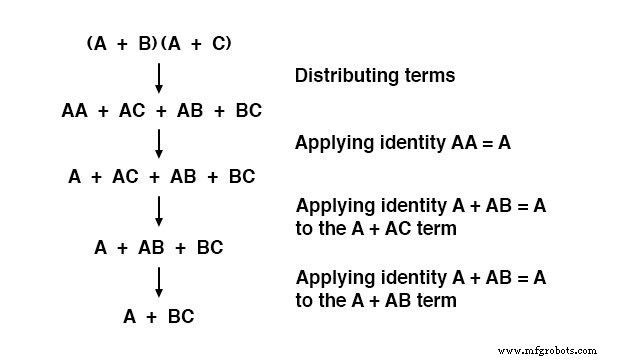
总而言之,这里是本节阐述的布尔化简的三个新规则:
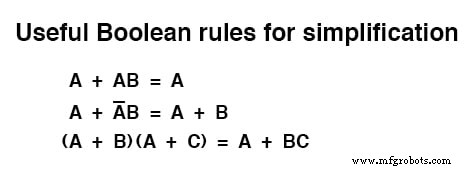
相关工作表:
- 布尔代数工作表
工业技术


