布尔运算
让我们通过将数字相加来开始我们对布尔代数的探索:
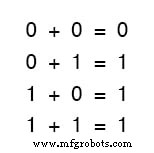
对于任何熟悉基本加法的人来说,前三个和非常有意义。
然而,最后一个总和很可能比数字电子学中的任何其他单一陈述更容易造成混乱,因为它似乎与数学的基本原理背道而驰。
嗯,它确实违反了实数的加法原理,但不违反布尔数。
请记住,在布尔代数的世界中,任何数量和任何算术运算只有两个可能的值:1 或 0。
在布尔值的范围内没有“2”这样的东西。由于和“1+1”肯定不是0,所以经过消元一定是1。
我们添加多少或几个术语也没有关系。考虑以下总和:
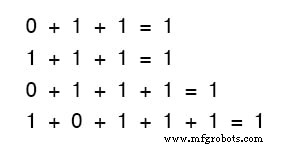
或门
仔细看看第一组方程中的两项总和。
你觉得这个模式很熟悉吗?这应该!它与 OR 门的真值表中看到的 1 和 0 的模式相同。
换句话说,布尔加法对应于“或”门的逻辑功能,以及并行开关触点:
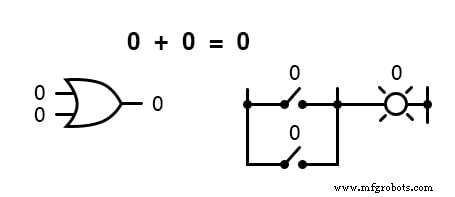
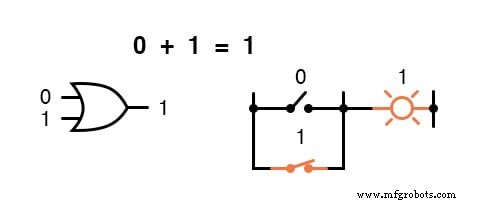
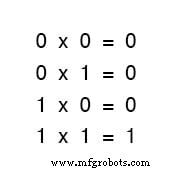
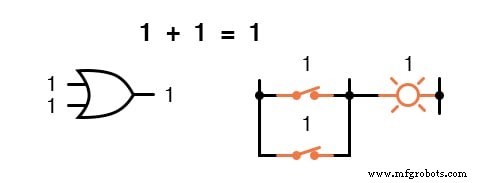
布尔数学领域没有减法这种东西。
减法意味着负数的存在:5 - 3 与 5 + (-3) 相同 , 并且在布尔代数中禁止使用负数。
布尔数学中也没有除法这样的东西,因为除法实际上只不过是复合减法 ,就像乘法是复合加法 .
与门
乘法在布尔代数中有效,幸运的是它与实数代数相同:乘以 0 是 0 , 以及任何乘以 1 保持不变:
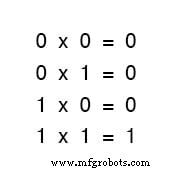
这组方程对您来说也应该很熟悉:它与 AND 门的真值表中的模式相同。
换句话说,布尔乘法对应于“AND ” 门,以及串联开关触点:
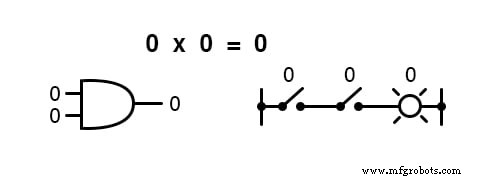
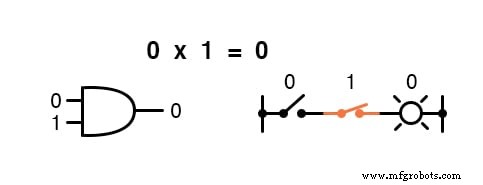
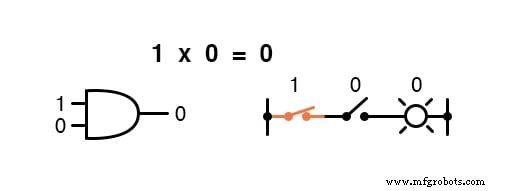
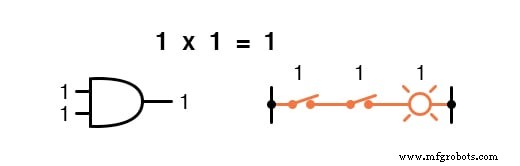
与“普通”代数一样,布尔代数使用字母来表示变量。
然而,与“普通”代数不同的是,布尔变量总是大写字母,从不小写。
因为它们只允许拥有两个可能值中的一个,要么 1 或 0 , 每个变量都有一个 补码 :与其值相反。
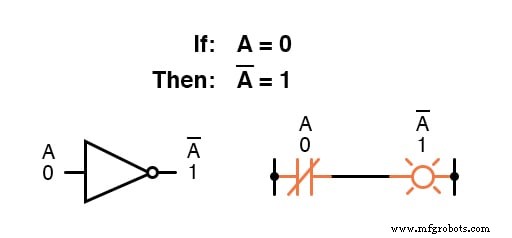
例如,如果变量“A ” 的值为 0 , 那么 A 的补码 值为 1 .
布尔表示法使用变量字符上方的横杠来表示补码,如下所示:
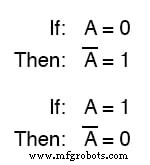
非门
在书面形式中,“A”的补语 ”表示为“A-not ”或“A-bar ”。有时用“素数”符号来表示互补。
例如,A ’将是 A 的补码 , 与在微积分中使用素数符号表示微分而不是分数符号 d/dt 非常相似 .
不过,通常情况下,“条”符号比“素数”使用更广泛 ”符号,其原因将在本章后面更加明显。
布尔互补以 NOT 门 的形式找到等价性 ,或常闭开关或继电器触点:
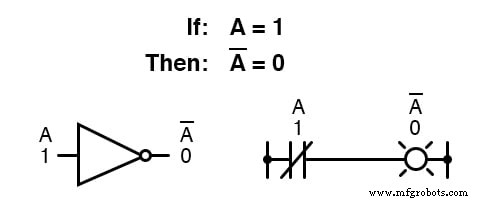
布尔量的基本定义导致了加法和乘法的简单规则,并排除了作为有效算术运算的减法和除法。
我们有一个用于表示布尔变量及其补码的符号系统。在下一节中,我们将继续开发布尔恒等式。
评论:
- 布尔加法等价于 OR 逻辑功能,以及并联开关触点。
- 布尔乘法等价于AND 逻辑功能,以及串联开关触点。
- 布尔互补等价于 NOT 逻辑函数,以及常闭 继电器触点。
相关工作表:
- 布尔代数工作表
工业技术


