串联电阻-电感电路

在上一节中，我们探讨了在简单的仅电阻器和仅电感器交流电路中会发生什么。现在我们将把这两个组件串联在一起并研究其效果。

串联电阻电感电路示例

以这个电路为例来配合：

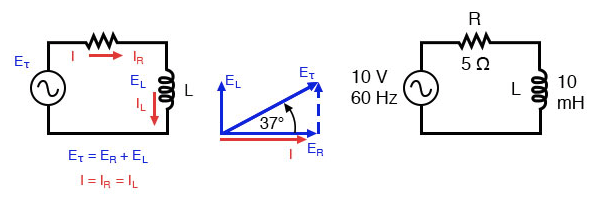
串联电阻电感电路：电流滞后施加电压 0o 到 90o。

无论频率如何，电阻器都会对交流电流提供 5 Ω 的电阻，而电感器将对 60 Hz 的交流电流提供 3.7699 Ω 的电抗。

由于电阻器的阻值为实数（5 Ω ∠ 0°，或 5 + j0 Ω），而电感器的电抗为虚数（3.7699 Ω ∠ 90°，或 0 + j3.7699 Ω），因此这两个分量将是一个对立电流，等于两个数的复数和。

这种组合对立将是电阻和电抗的矢量组合。为了简洁地表达这种对立，我们需要一个比单独电阻或电抗更全面的术语来表示对电流的对立。

这个术语叫做阻抗 ，其符号为Z，也以欧姆为单位表示，就像电阻和电抗一样。在上例中，总电路阻抗为：

欧姆定律中的电阻

正如您所料，阻抗与电压和电流有关，其方式类似于欧姆定律中的电阻：

事实上，这是一种比直流电子学 (E=IR) 所教授的欧姆定律更全面的形式，正如阻抗是一种比电阻更全面的反对电流的表达方式。 任何 电阻和任何电抗，单独或组合（串联/并联），可以并且应该表示为交流电路中的单个阻抗。

要计算上述电路中的电流，我们首先需要为电压源提供一个相角参考，一般假定为零。 （阻性阻抗和感性阻抗的相角总是 分别为 0° 和 +90°，与给定的电压或电流相角无关）。

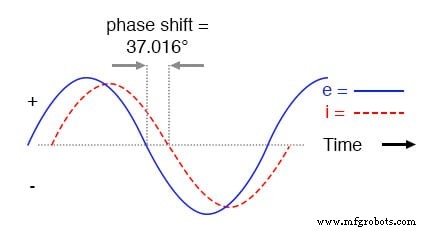
与纯电感电路一样，电流波滞后于（源的）电压波，尽管这次滞后没有那么大：只有 37.016°，而在纯电感电路中则是完整的 90° .

串联 L-R 电路中的电流滞后于电压。

对于电阻器和电感器，电压和电流之间的相位关系没有改变。电阻器两端的电压与通过它的电流同相（0° 偏移），而电感器两端的电压与通过它的电流异相 +90°。我们可以用数学方法验证这一点：

电阻两端的电压与通过它的电流具有完全相同的相角，告诉我们 E 和 I 同相（仅适用于电阻）。

电感两端的电压相位角为 52.984°，而通过电感的电流相位角为 -37.016°，两者相差 90°。这告诉我们 E 和 I 仍然相差 90°（仅针对电感器）。

使用基尔霍夫电压定律

我们还可以从数学上证明这些复数值加在一起构成总电压，正如基尔霍夫电压定律所预测的那样：

使用 SPICE 计算

让我们用 SPICE 检查计算的有效性：

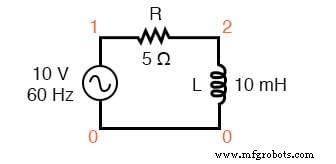
香料电路：R-L。

v1 1 0 ac 10 sin r1 1 2 5 l1 2 0 10m .ac 林 1 60 60 .print ac v(1,2) v(2,0) i(v1) .print ac vp(1,2) vp(2,0) ip(v1) 。结尾 

频率 v(1,2) v(2) i(v1) 6.000E+01 7.985E+00 6.020E+00 1.597E+00 频率 vp(1,2) vp(2) ip(v1) 6.000E+01 -3.702E+01 5.298E+01 1.430E+0 

请注意，与直流电路一样，SPICE 输出电流数字就好像它们与电源电压为负值（180° 异相）。我们得到的相位角不是 -37.016°，而是 143°（-37° + 180°）。

这只是 SPICE 的一个特性，并不代表电路仿真本身的任何重要内容。请注意电阻器和电感器电压相位读数与我们的计算结果如何匹配（分别为 -37.02° 和 52.98°），正如我们预期的那样。

有了所有这些数字来跟踪即使是这样一个简单的电路，使用“表格”方法对我们来说是有益的。将表格应用于这个简单的串联电阻 - 电感电路将如此进行。

首先，为 E/I/Z 数字绘制一个表格，并在这些术语中插入所有组件值（换句话说，不要将分别以欧姆和亨为单位的实际电阻或电感值插入表中；而是将它们转换转化为复数的阻抗并将其写入）：

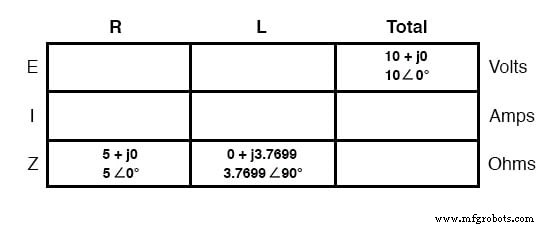
虽然不是必需的，但我发现写两者很有帮助 表中每个量的矩形和极坐标形式。如果您使用的计算器能够执行复杂的算术运算，而无需在直角和极坐标之间进行转换，那么这个额外的文档是完全没有必要的。

然而，如果你被迫执行复杂的算术“普通”（矩形形式的加减法，极坐标形式的乘法和除法），用两种形式写出每个数量确实很有用。

现在我们的“给定”数字被插入到表中的相应位置，我们可以像处理 DC 一样继续：从各个阻抗确定总阻抗。由于这是一个串联电路，我们知道反对电流流动（电阻或 阻抗）相加形成总对立：

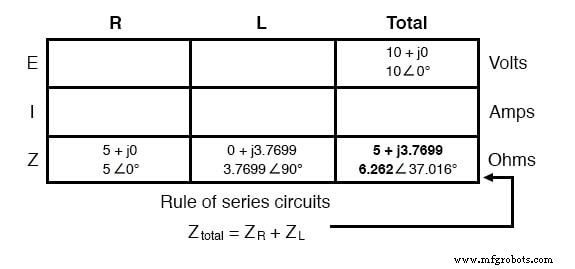
现在我们知道了总电压和总阻抗，我们可以应用欧姆定律 (I=E/Z) 来确定总电流：

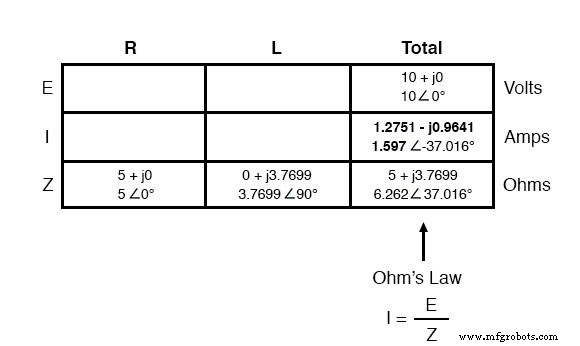
与 DC 一样，串联 AC 电路中的总电流由所有组件平均分配。这仍然是正确的，因为在串联电路中只有一条电流通过路径，因此它们的流动速率必须始终一致。因此，我们可以将电流的数字转移到电阻器和电感器的列中：

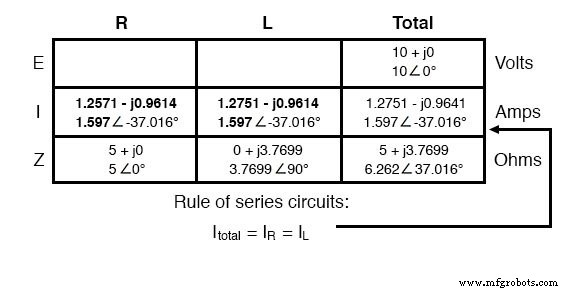
现在剩下的就是分别穿过电阻器和电感器的压降。这是通过使用欧姆定律 (E=IZ) 完成的，在表格的每一列中垂直应用：

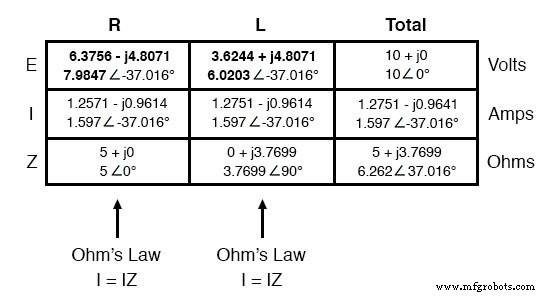
这样，我们的桌子就完成了。我们在直流电路分析中应用的完全相同的规则也适用于交流电路，但需要注意的是，所有量都必须以复数形式而不是标量形式表示和计算。

只要在我们的计算中正确地表示了相移，我们在处理基本交流电路分析与直流电路的方法上就没有根本区别。

现在是回顾这些计算数字与实际仪器电压和电流测量给出的读数之间的关系的好时机。

此处与实际测量直接相关的数字是极坐标表示法 ，不是长方形！换句话说，如果你在这个电路中的电阻两端连接一个电压表，它会指示 7.9847 伏特，而不是 6.3756（真正的矩形）或 4.8071（假想的矩形）伏特。

为了用图形术语来描述这一点，测量仪器只是告诉您该特定量（电压或电流）的矢量有多长。

矩形符号虽然便于算术加法和减法，但相对于实际测量而言，它是一种比极坐标更抽象的符号形式。正如我之前所说，为了方便数学计算，我将在我的交流电路表中指出每个量的极坐标和矩形形式。

这不是绝对必要的，但可能对那些没有高级计算器好处的人有所帮助。如果我们限制自己只使用一种符号形式，最好的选择是 polar，因为它是唯一一种可以与实际测量直接相关的符号。

给定电阻 (R) 和感抗 (XL)，可以计算串联 R-L 电路的阻抗 (Z)。由于 E=IR、E=IXL 和 E=IZ，电阻、电抗和阻抗分别与电压成正比。因此，电压相量图可以用类似的阻抗图代替。

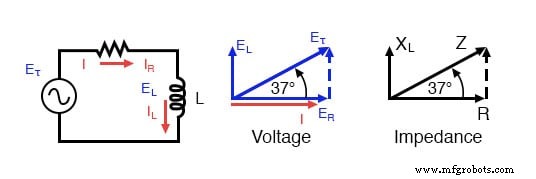
系列：R-L 电路阻抗相量图。

示例： 给定：一个 40 Ω 电阻器与一个 79.58 毫亨电感器串联。求出 60 赫兹处的阻抗。

<前> XL =2πfL XL =2π·60·79.58×10-3 XL =30 Ω Z =R + jXL Z =40 + j30 |Z| =sqrt(402 + 302) =50 Ω ∠Z =反正切(30/40) =36.87° Z =40 + j30 =50∠36.87°

评论：

• 阻抗 是对抗电流的总度量，是（“实”）电阻和（“虚”）电抗的复（矢量）和。它由字母“Z”表示，以欧姆为单位，就像电阻 (R) 和电抗 (X) 一样。
• 阻抗 (Z) 的管理就像串联电路分析中的电阻 (R) 一样：串联阻抗相加形成总阻抗。请务必以复杂（非标量）形式执行所有计算！ ZTotal=Z1 + Z2 + 。 . .锌
• 纯电阻阻抗的相位角始终为 0°（ZR =R Ω ∠ 0°）。
• 纯感性阻抗的相位角始终恰好为 +90°（ZL =XL Ω ∠ 90°）。
• 交流电路的欧姆定律：E =IZ； I =E/Z; Z =E/I
• 当电阻器和电感器在电路中混合在一起时，总阻抗的相位角将介于 0° 和 +90° 之间。电路电流的相位角介于 0° 和 -90° 之间。
• 串联交流电路具有与串联直流电路相同的基本特性：整个电路中的电流是均匀的，电压降相加形成总电压，而阻抗相加形成总阻抗。

相关工作表：

• 电感工作表
• 电阻、电抗和阻抗工作表
• 感抗工作表