方​​波信号

已经发现任何 重复的非正弦波形可以等同于各种幅度和频率的直流电压、正弦波和/或余弦波（具有 90 度相移的正弦波）的组合。

无论所讨论的波形多么奇怪或多么复杂，这都是正确的。只要它随着时间的推移有规律地重复，就可以还原为这一系列的正弦波。

特别是，已经发现方波在数学上等同于相同频率的正弦波加上幅度递减的奇数倍频正弦波的无穷级数之和：

这个关于波形的真相乍一看似乎太奇怪了，难以置信。但是，如果方波实际上是无限系列的正弦波谐波相加，按理说我们应该能够通过将几个正弦波谐波相加来产生方波的近似值来证明这一点。

这种推理不仅合理，而且很容易用 SPICE 证明。

我们将要模拟的电路只不过是几个串联连接在一起的适当幅度和频率的正弦波交流电压源。我们将使用 SPICE 绘制连续添加的电压源的电压波形，如下所示：

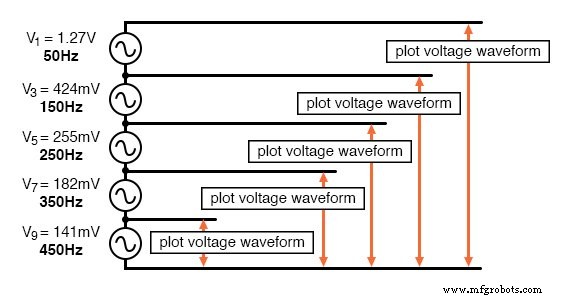
方波由谐波之和近似。

在这个特殊的 SPICE 仿真中，我将串联的 1 次、3 次、5 次、7 次和 9 次谐波电压源相加，共五个交流电压源。基频为 50 Hz，每个谐波当然是该频率的整数倍。

幅度（电压）数字不是随机数；相反，它们是通过频率序列中所示的方程得出的（对于每个增加的奇次谐波，分数 4/π 乘以 1、1/3、1/5、1/7 等）。

构建方波 v1 1 0 sin (0 1.27324 50 0 0) 一阶谐波 (50 Hz) v3 2 1 sin (0 424.413m 150 0 0) 三次谐波 v5 3 2 sin (0 254.648m 250 0 0) 5 次谐波 v7 4 3 sin (0 181.891m 350 0 0) 7 次谐波 v9 5 4 sin (0 141.471m 450 0 0) 9 次谐波 r1 5 0 10k .tran 1m 20m .plot tran v(1,0) 绘制一阶谐波 .plot tran v(2,0) 绘制 1 次 + 3 次谐波 .plot tran v(3,0) 绘制 1st + 3rd + 5th 谐波 .plot tran v(4,0) 绘制 1st + 3rd + 5th + 7th 谐波 .plot tran v(5,0) 绘制第 1 个 + . . . + 9 次谐波 。结尾 

我将从这里逐步叙述分析，解释我们正在研究的是什么。在第一幅图中，我们看到了 50 Hz 的基频正弦波本身。它只是一个纯正弦形状，没有额外的谐波成分。这是理想交流电源产生的那种波形：

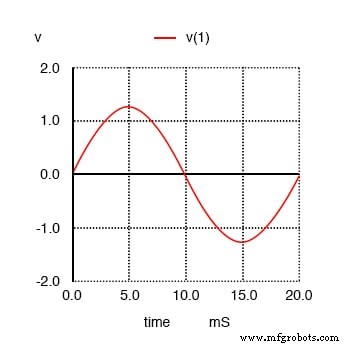
纯 50 Hz 正弦波。

接下来，我们看看当这个干净简单的波形与三次谐波（3 倍 50 Hz 或 150 Hz）组合时会发生什么。突然间，它看起来不再像一个干净的正弦波了：

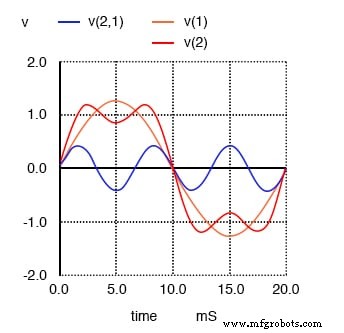
第一次 (50 Hz) 和第三次 (150 Hz) 谐波的总和近似为 50 Hz 方波。

正负周期之间的上升和下降时间现在更加陡峭，波峰更接近于像方波一样平坦。观察添加下一个奇次谐波频率时会发生什么：

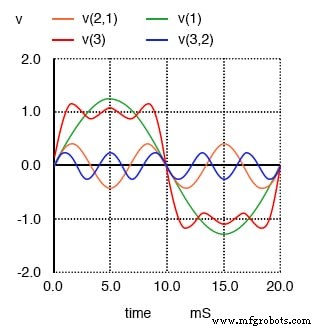
1 次、3 次和 5 次谐波的总和近似于方波。

这里最显着的变化是波峰如何变得更加平坦。波浪的每一端都有更多的波峰和波峰，但这些波峰的振幅比以前小。再次观看，我们将下一个奇次谐波波形添加到混音中：

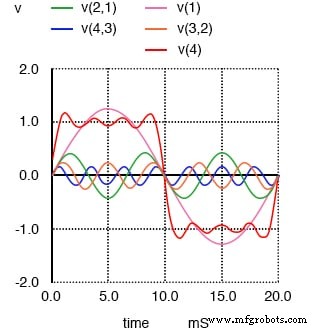
1 次、3 次、5 次和 7 次谐波的总和近似于方波。

在这里，我们可以看到波在每个峰值处变得更平坦。最后，在我们的电路中加入第 9 次谐波，即第 5 次正弦波电压源，我们得到这样的结果：

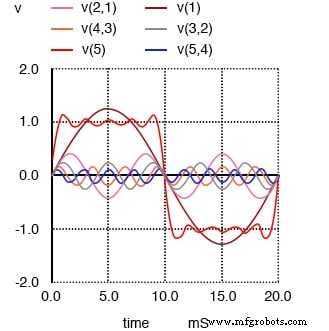
1 次、3 次、5 次、7 次和 9 次谐波的总和近似于方波。

将前五个奇次谐波波形加在一起的最终结果（当然都是在适当的幅度下）是方波的近似值。这样做的目的是为了说明我们如何从多个不同频率的正弦波向上构建方波，以证明纯方波实际上等效于系列 正弦波。

当方波交流电压施加到具有电抗元件（电容器和电感器）的电路时，这些元件会产生反应，就好像它们暴露在几个不同频率的正弦波电压下一样，实际上它们确实如此。

重复的非正弦波等效于一定系列的附加直流电压、正弦波和/或余弦波的事实是波如何工作的结果：所有与波相关的现象（电或其他）的基本特性。

将非正弦波减少到这些组成频率的数学过程称为傅立叶分析 ，其中的细节远远超出了本文的范围。然而，已经创建了计算机算法来对真实波形进行高速分析，并且其在交流电能质量和信号分析中的应用非常广泛。

SPICE 能够对波形进行采样，并通过傅立叶变换将其分解为组成它的正弦波谐波 算法，将频率分析输出为数字表。让我们在方波上试试这个，我们已经知道它是由奇次谐波正弦波组成的：

方波分析网表 v1 1 0 脉冲 (-1 1 0 .1m .1m 10m 20m) r1 1 0 10k .tran 1m 40m .plot tran v(1,0) .四 50 v(1,0) 。结尾 

脉冲 描述电压源 v1 的网表行中的选项 指示 SPICE 模拟方形“脉冲”波形，在这种情况下，该波形是对称的（每个半周期的时间相等）并且峰值幅度为 1 伏。首先，我们将绘制要分析的方波：

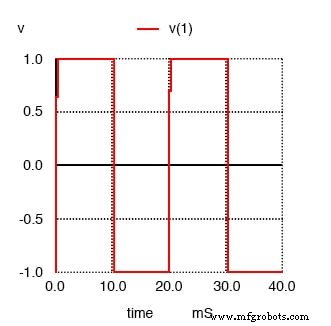
SPICE 傅立叶分析的方波

接下来，我们将打印 SPICE 为这个方波生成的傅立叶分析：

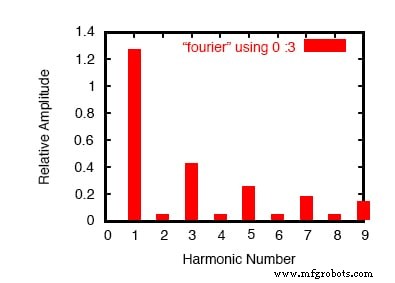
瞬态响应的傅立叶分量 v(1) 直流分量 =-2.439E-02 谐波频率傅立叶归一化相位归一化 无 (hz) 分量 分量 (deg) 相位 (deg) 1 5.000E+01 1.274E+00 1.000000 -2.195 0.000 2 1.000E+02 4.892E-02 0.038415 -94.390 -92.195 3 1.500E+02 4.253E-01 0.333987 -6.585 -4.390 4 2.000E+02 4.936E-02 0.038757 -98.780 -96.585 5 2.500E+02 2.562E-01 0.201179 -10.976 -8.780 6 3.000E+02 5.010E-02 0.039337 -103.171 -100.976 7 3.500E+02 1.841E-01 0.144549 -15.366 -13.171 8 4.000E+02 5.116E-02 0.040175 -107.561 -105.366 9 4.500E+02 1.443E-01 0.113316 -19.756 -17.561 总谐波失真 =43.805747% 

傅立叶分析结果图。

在这里，（上图）SPICE 将波形分解为高达九次谐波的正弦频率频谱，加上标记为 DC 分量 的小直流电压 .

我必须将基频告知 SPICE（对于周期为 20 毫秒的方波，该频率为 50 Hz），因此它知道如何对谐波进行分类。请注意所有偶次谐波（2 次、4 次、6 次、8 次）的数字有多小，以及奇次谐波的幅度如何减小（1 次最大，9 次最小）。

“傅立叶变换”的相同技术通常用于计算机化的电力仪表，对交流波形进行采样并确定其谐波含量。一种常见的计算机算法（执行任务的程序步骤序列）是快速傅立叶变换 或 FFT 功能。

你不必关心这些计算机程序究竟是如何工作的，但要注意它们的存在和应用。

SPICE 中用于分析波形谐波含量的相同数学技术也可以应用于音乐的技术分析：将任何特定声音分解为其组成的正弦波频率。

事实上，您可能已经看到了一种设计用于执行此操作的设备，而没有意识到它是什么！ 图形均衡器 是一种高保真立体声设备，用于控制（有时显示）音乐谐波内容的性质。

配备多个旋钮​​或滑动杆，均​​衡器能够有选择地衰减（降低）音乐中某些频率的振幅，以“定制”声音以造福听众。通常，每个控制杆旁边都会有一个“条形图”显示，显示每个特定频率的幅度。

Hi-Fi 音频图形均衡器。

一种严格构建以显示而不是控制混合频率信号的每个频率范围的幅度的设备通常称为频谱分析仪 .

频谱分析仪的设计可能简单到一组“滤波器”电路（详见下一章），旨在将不同的频率相互分离，也可能复杂到运行 FFT 算法的专用数字计算机。以数学方式将信号分解为其谐波分量。

频谱分析仪通常设计用于分析极高频信号，例如由无线电发射机和计算机网络硬件产生的信号。在这种形式下，它们通常具有示波器的外观：

频谱分析仪将幅度显示为频率的函数。

与示波器一样，频谱分析仪使用 CRT（或模拟 CRT 的计算机显示器）来显示信号图。

与示波器不同，此图是幅度与频率的关系图 而不是幅度随时间 .本质上，频率分析仪为操作员提供信号的波特图：工程师可能称之为频域 而不是时域 分析。

术语“域”是数学上的：描述图形水平轴的复杂词。因此，示波器的幅度（垂直）随时间（水平）变化图是“时域”分析，而频谱分析仪的幅度（垂直）随频率（水平）变化图是“频域”分析。

当我们使用 SPICE 在一定频率范围内绘制信号幅度（电压或电流幅度）时，我们正在执行频域 分析。

请注意上次 SPICE 仿真的傅立叶分析如何不“完美”。理想情况下，所有偶次谐波的幅度应该绝对为零，直流分量也应该如此。同样，这与其说是 SPICE 的怪癖，不如说是一般波形的属性。

可以绝对精确地分析无限持续时间（无限循环数）的波形，但计算机可用于分析的循环越少，分析的精确度就越低。只有当我们有一个完整描述波形的方程时，傅立叶分析才能将其简化为一系列确定的正弦波形。

波循环的次数越少，其频率就越不确定。将这个概念推向极端，一个短脉冲——一个甚至不能完成一个周期的波形——实际上没有频率 ，而是充当无限范围的频率。这个原则对所有人来说都是通用的 基于波的现象，而不仅仅是交流电压和电流。

可以说周期数和波形频率分量的确定性直接相关。

我们可以通过让波不断振荡许多周期来提高分析的精度，结果将是更符合理想情况的频谱分析。在下面的分析中，为了简洁起见，我省略了波形图——它只是一个非常长的方波：

方波 v1 1 0 脉冲 (-1 1 0 .1m .1m 10m 20m) r1 1 0 10k .option limpts=1001 .tran 1m 1 .plot tran v(1,0) .四 50 v(1,0) 。结尾 瞬态响应的傅立叶分量 v(1) 直流分量 =9.999E-03 谐波频率傅立叶归一化相位归一化 无 (hz) 分量 分量 (deg) 相位 (deg) 1 5.000E+01 1.273E+00 1.000000 -1.800 0.000 2 1.000E+02 1.999E-02 0.015704 86.382 88.182 3 1.500E+02 4.238E-01 0.332897 -5.400 -3.600 4 2.000E+02 1.997E-02 0.015688 82.764 84.564 5 2.500E+02 2.536E-01 0.199215 -9.000 -7.200 6 3.000E+02 1.994E-02 0.015663 79.146 80.946 7 3.500E+02 1.804E-01 0.141737 -12.600 -10.800 8 4.000E+02 1.989E-02 0.015627 75.529 77.329 9 4.500E+02 1.396E-01 0.109662 -16.199 -14.399 

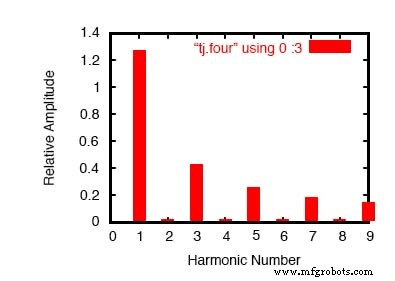
改进了傅立叶分析。

请注意此分析（上图）如何显示每个偶次谐波频率正弦波的直流分量电压较少，振幅较低，这一切都是因为我们让计算机对波的更多周期进行采样。同样，第一次分析的不精确与其说是 SPICE 中的缺陷，不如说是波和信号分析的基本属性。

评论：

• 方波相当于在相同（基本）频率的正弦波添加到幅度递减的奇数倍正弦波谐波的无穷系列中。
• 存在能够对波形进行采样并确定其组成正弦分量的计算机算法。 傅立叶变换 算法（特别是快速傅立叶变换 , 或 FFT ) 常用于计算机电路仿真程序（例如 SPICE）和用于确定电能质量的电子计量设备。

相关工作表：

• 方波信号工作表