其他波形

尽管看起来很奇怪，任何 重复的非正弦波形实际上相当于一系列不同幅度和频率的正弦波形加在一起。方波是一种非常常见且易于理解的情况，但并非唯一。

电子功率控制器件，例如晶体管和可控硅整流器 (SCRs ) 通常会产生电压和电流波形，这些波形基本上是来自电源的“干净”（纯）正弦波交流电的斩波版本。

这些设备能够突然改变 它们的电阻随着控制信号电压或电流的应用而变化，因此几乎在瞬间“开启”或“关闭”，产生的电流波形与为电路供电的电源电压波形几乎没有相似之处。

由于通过电路阻抗的非正弦电流产生的电压降，这些电流波形会导致其他电路组件的电压波形发生变化。

非线性组件

使交流电压或电流的正常正弦波形失真的电路元件称为非线性 .非线性元件（例如 SCR）在电力电子设备中得到广泛应用，因为它们能够调节大量电力而不会散发太多热量。

虽然从能源效率的角度来看这是一个优势，但它们引入的波形失真可能会导致问题。

这些非正弦波形，无论其实际形状如何，都相当于一系列较高（谐波）频率的正弦波形。

如果电路设计者不考虑，这些由电子开关元件产生的谐波波形可能会导致电路行为不稳定。

由于计算机和高效灯等“开关”负载产生的交流电源线电压的正弦波形失真，在电力行业中观察到变压器和电机过热变得越来越普遍。

这不是理论练习：它非常真实，而且可能非常麻烦。

在本节中，我将研究一些更常见的波形，并使用 SPICE 通过傅立叶分析显示它们的谐波分量。

交流电源系统中产生谐波的一种非常常见的方式是将交流电转换或“整流”为直流电。这通常是通过称为二极管的组件完成的 ，只允许电流在一个方向通过。

半波整流

最简单的 AC/DC 整流类型是半波 ，其中单个二极管阻止一半的交流电流（随着时间的推移）通过负载。 （下图）

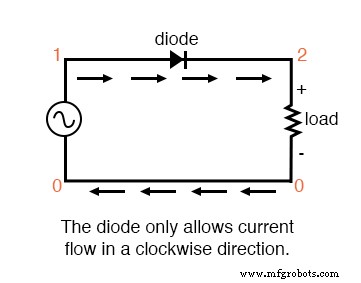
半波整流器

半波整流器 v1 1 0 sin(0 15 60 0 0) 加载 2 0 10k d1 1 2 mod1 .model mod1 d .tran .5m 17m .plot tran v(1,0) v(2,0) .四 60 v(1,0) v(2,0) 。结尾 

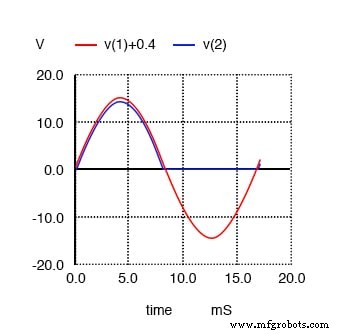
半波整流波形。为了清晰起见，V(1)+0.4 将正弦波输入 V(1) 上移。这不是模拟的一部分。

首先，我们将看到 SPICE 如何分析源波形，纯正弦波电压：（下图）

瞬态响应的傅立叶分量 v(1) 直流分量 =8.016E-04 谐波频率傅立叶归一化相位归一化 无 (hz) 分量 分量 (deg) 相位 (deg) 1 6.000E+01 1.482E+01 1.000000 -0.005 0.000 2 1.200E+02 2.492E-03 0.000168 -104.347 -104.342 3 1.800E+02 6.465E-04 0.000044 -86.663 -86.658 4 2.400E+02 1.132E-03 0.000076 -61.324 -61.319 5 3.000E+02 1.185E-03 0.000080 -70.091 -70.086 6 3.600E+02 1.092E-03 0.000074 -63.607 -63.602 7 4.200E+02 1.220E-03 0.000082 -56.288 -56.283 8 4.800E+02 1.354E-03 0.000091 -54.669 -54.664 9 5.400E+02 1.467E-03 0.000099 -52.660 -52.655 

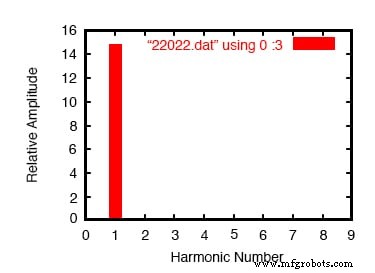
正弦波输入的傅里叶分析

请注意上表中这个正弦波形的极小谐波和直流分量，但太小而无法在上面的谐波图中显示。

理想情况下，除了基本频率显示（完美的正弦波）之外什么都没有，但我们的傅立叶分析数字并不完美，因为 SPICE 没有对无限持续时间的波形进行采样的奢侈。接下来，我们将其与负载电阻两端的半波“整流”电压的傅立叶分析进行比较：（下图）

瞬态响应的傅立叶分量 v(2) 直流分量 =4.456E+00 谐波频率傅立叶归一化相位归一化 无 (hz) 分量 分量 (deg) 相位 (deg) 1 6.000E+01 7.000E+00 1.000000 -0.195 0.000 2 1.200E+02 3.016E+00 0.430849 -89.765 -89.570 3 1.800E+02 1.206E-01 0.017223 -168.005 -167.810 4 2.400E+02 5.149E-01 0.073556 -87.295 -87.100 5 3.000E+02 6.382E-02 0.009117 -152.790 -152.595 6 3.600E+02 1.727E-01 0.024676 -79.362 -79.167 7 4.200E+02 4.492E-02 0.006417 -132.420 -132.224 8 4.800E+02 7.493E-02 0.010703 -61.479 -61.284 9 5.400E+02 4.051E-02 0.005787 -115.085 -114.889 

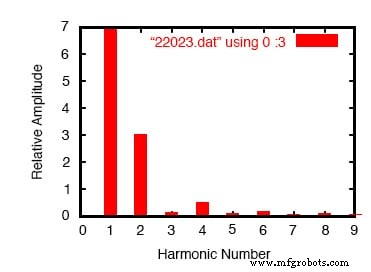
傅立叶分析半波输出

请注意此分析中相对较大的偶次多次谐波。通过切除一半的交流波，我们从原始的纯正弦波中引入了几个高频正弦（实际上是余弦）波形的等效波形。

还要注意较大的直流分量：4.456 伏。因为我们的交流电压波形已经过“整流”（只允许在负载的一个方向上推动，而不是来回推动），它的表现更像直流。

全波整流

另一种交流/直流转换方法称为全波 （下图），正如您可能已经猜到的那样，它利用来自电源的整个交流电源周期，反转半个交流周期的极性，使电子始终以相同的方向流过负载。

我不会详细说明这是如何完成的，但我们可以通过 SPICE 检查波形（下图）及其谐波分析：

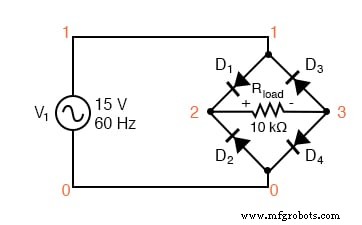
全波整流电路

全波桥式整流器 v1 1 0 sin(0 15 60 0 0) 加载 2 3 10k d1 1 2 mod1 d2 0 2 mod1 d3 3 1 mod1 d4 3 0 mod1 .model mod1 d .tran .5m 17m .plot tran v(1,0) v(2,3) .四 60 v(2,3) 。结尾 

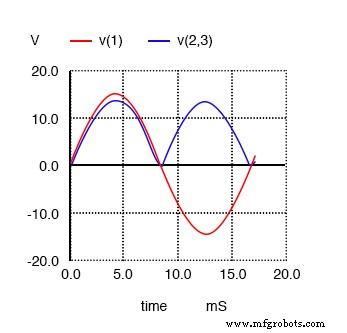
全波整流器的波形

瞬态响应的傅立叶分量 v(2,3) 直流分量 =8.273E+00 谐波频率傅立叶归一化相位归一化 无 (hz) 分量 分量 (deg) 相位 (deg) 1 6.000E+01 7.000E-02 1.000000 -93.519 0.000 2 1.200E+02 5.997E+00 85.669415 -90.230 3.289 3 1.800E+02 7.241E-02 1.034465 -93.787 -0.267 4 2.400E+02 1.013E+00 14.465161 -92.492 1.027 5 3.000E+02 7.364E-02 1.052023 -95.026 -1.507 6 3.600E+02 3.337E-01 4.767350 -100.271 -6.752 7 4.200E+02 7.496E-02 1.070827 -94.023 -0.504 8 4.800E+02 1.404E-01 2.006043 -118.839 -25.319 9 5.400E+02 7.457E-02 1.065240 -90.907 2.612 

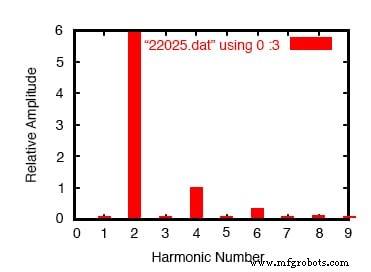
全波整流输出的傅里叶分析

有什么不同！根据 SPICE 的傅立叶变换，我们在这个波形上有一个 2 次谐波分量，它是原始交流电源频率幅度的 85 倍以上！

该波的直流分量显示为 8.273 伏（几乎是半波整流电路的两倍），而二次谐波的幅度几乎为 6 伏。注意表格下方的所有其他谐波。

实际上，奇次谐波在某些较高频率处比在较低频率处更强，这很有趣。

如您所见，开始时可能是简洁的交流正弦波，但经过几个电子元件后，可能会变成一团复杂的谐波。

虽然所有这些傅立叶变换背后的复杂数学对于电子电路的初学者来说并不是必须要理解的，但最重要的是了解工作原理并掌握谐波信号可能对电路产生的实际影响。

本章的最后一节将探讨电路中谐波频率的实际影响，但在此之前，我们将仔细研究波形及其各自的谐波。

评论：

• 任何 波形，只要它是重复的，就可以简化为一系列相加的正弦波形。不同的波形由不同的正弦波谐波混合组成。
• 交流到直流的整流是工业电力系统中非常常见的谐波来源。