叠加定理 - 具有求解示例的电路分析
叠加定理 - 带求解示例的分步指南
什么是叠加定理?
叠加定理 用于解决具有多种能源的复杂网络。通过单独计算每个源的影响来确定元件上的电压和电流是一个重要的概念。并综合各来源的影响,得到电路元件的实际电压和电流。
叠加定理表明;
换句话说,我们一次只考虑一个独立的来源。因此,我们需要删除其他来源。电压源是短路的,电流源是开路的,用于理想源。如果给定源的内阻,则需要考虑电路。
叠加定理只适用于遵循欧姆定律的电路。
- 相关文章:戴维南定理。带有已解决示例的分步指南
什么时候使用叠加定理?
网络必须遵循以下要求才能应用叠加定理。
- 电路中使用的元件必须是线性的。这意味着,对于电阻器,电流与电压成正比;对于电感器,磁链与电流成正比。因此,电阻器、电感器和电容器是线性元件。但是二极管、三极管不是线性元件。
- 电路元件必须是双边元件。这意味着,电流的大小与能源的极性无关。
- 借助叠加定理,我们可以求出流经元件的电流、电阻压降和节点电压。但是我们找不到元素散发的力量。
- 相关文章:诺顿定理。带有已解决示例的分步指南
叠加定理的步骤
步骤一 找出网络中可用的许多独立来源。
第二步 选择任何一种来源并消除所有其他来源。如果网络包含任何依赖源,则无法消除它。在整个计算过程中保持原样。
如果你认为所有的能源都是理想的来源,你就不需要考虑内阻了。并直接短路电压源和开路电流源。但万一,如果给定了源内阻,就必须更换内阻。
第三步 现在,在一个电路中,只有一个独立的能源存在。你需要找到电路中只有一种能源的响应。
第四步 对网络中可用的所有能源重复步骤 2 和 3。如果有三个独立的来源,则需要将这些步骤重复 3 次。并且每次你得到一些响应的价值。
第五步 现在,通过各个来源获得的代数和来组合所有响应。您将获得网络特定元素的最终响应值。如果您需要查找其他元素的响应,则需要针对该元素再次执行这些步骤。
- 相关文章:SUPERMESH 电路分析 - 逐步解决示例
叠加定理求解示例
示例:
让我们通过例子来了解叠加定理的工作原理。利用叠加定理求出通过给定网络中8Ω电阻的电流(IL)。
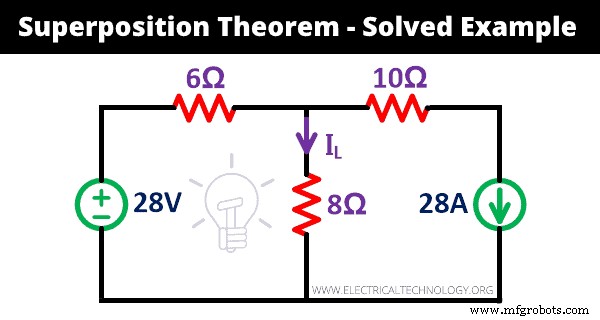
解决方案:
步骤一 如上图所示,给定一个电压源和一个电流源。因此,我们需要重复该过程两次。
第二步 首先,我们认为网络中存在 28V 电压源。因此,您需要通过开路端子移除电流源。在这里,我们将电流源视为理想的电流源。所以,我们不需要连接内阻。
剩下的电路如下图所示。
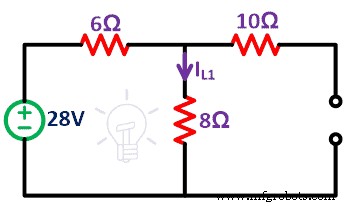
第三步 求电流(IL1)通过 8Ω 电阻。它只提供电压源的效果。
由于电流源开路,10Ω电阻没有电流通过。所以,网络只有一个循环。
将KVL应用于循环;
28 =6I L 1 + 8我 L 1
28 =14我 L 1
我 L 1 =28/14
我 L 1 =2A
第四步 现在,我们对当前源重复相同的过程。在这种情况下,我们通过短路来移除电压源。剩下的电路如下图所示。
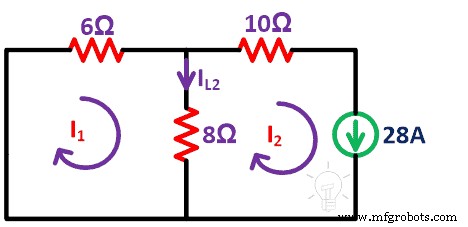
这里,我们要考虑两个循环。 I1 和 I2 是回路电流。并找到当前的IL2。
将KVL应用到loop-1;
0 =6我 1 + 8我 1 - 8我 2
14我 1 - 8我 2 =0
通过loop-2的电流是从电流源计算出来的。会的;
我 2 =28A
把这个值代入上式;
14我 1 - 8 (28) =0
我 1 =16A
现在,8Ω 电阻分支在两个环路中都很常见。所以,我们需要找到通过8Ω电阻的合成电流(IL2)。
我 L 2 =我 1 - 我 2
我 L 2 =16 - 28
我 L 2 =-12A
第五步 现在,我们通过电流的代数和来结合两种来源的影响。因此,通过 8Ω 电阻的总电流为 IL。在这里,电流的方向是最重要的。电流 IL2 有一个减号。这意味着在 28A 电源期间,电流以相反方向流动。我们不能改变方向。这就是我们在结合所有来源的同时进行代数求和的原因。
我 L =IL 1 - IL 2
我 L =2 + (-12)
我 L =-10A
这里,我们假设流过8Ω电阻的电流方向如图所示。减号表示相反的方向。电流量为8A。
- 相关文章:SUPERNODE 电路分析 - 逐步解决示例
叠加定理实验
叠加定理实验可以按照以下步骤进行。
瞄准
确定流过电阻的电流,验证叠加定理。
需要的组件
直流电源、电阻、直流万用表、连接线、面包板等
理论
叠加定理用于电路分析,以找出给定电路中元件上的电流和电压。当源数较多时,这个定理很有用。
根据叠加定理,元素的响应是各个能源响应的代数和。
首先,我们将计算通过给定网络中电阻器的电流。当所有源都连接时。之后,我们移除源并找到各个源的电流。最后,从单个源测量的电流总和类似于所有源连接的电流测量。
过程
我们考虑下图给出的线性双边电路。
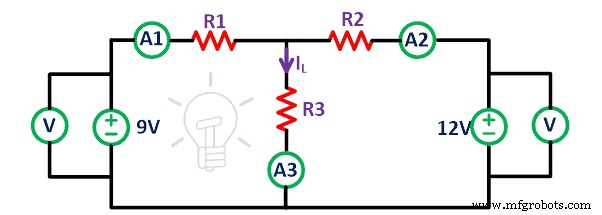
使用连接线连接面包板上的所有元件,如上述电路中给出的。将电流表与所有电阻器连接,以找到通过电阻器的电流。在这里,我们有两个电压源。
在第一种情况下,当电路中同时存在两个电压源时,测量通过所有电阻的电流。流过电阻R1、R2、R3的电流为I 1、我 2、我 3个。
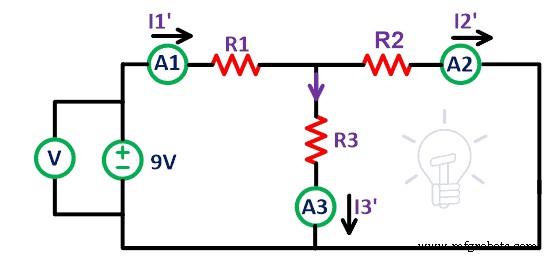
现在从电路中移除 12V 电压源。如上图所示短接端子 A'和 B'。这里我们假设电压源是理想的。因此,无需连接内阻。现在,测量当前的 I 1′,我 2′ 和 I 3′为分别通过电阻R1、R2、R3的电流。
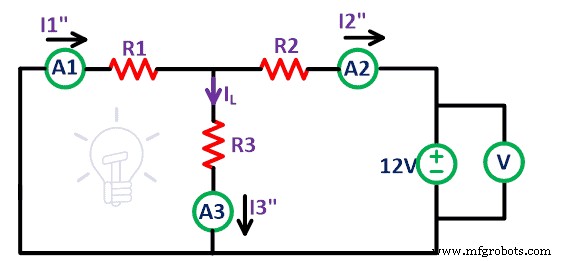
同理,去掉9V电压源,剩下的电路如上图所示。再次测量流过所有电阻的电流并将其命名为 I 1“,我 2“,和我 3“。
- 相关文章: 交流和直流电路的最大功率传输定理
把所有的值放在观察表下面。
观察表
| 源连接 | R1 | R2 | R3 |
| 两个源都已连接 | 我 1 | 我 2 | 我 3 |
| 只接了12V | 我 1' | 我 2′ | 我 3′ |
| 只接了9V | 我 1″ | 我 2″ | 我 3″ |
计算 :
我 1 =我 1′ + 我 1″
我 2 =我 2′ + 我 2″
我 3 =我 3′ + 我 3″
为了验证叠加定理,我们将单个电源连接时通过电阻的电流的代数和与两个电源连接在电路中时测量的电流进行比较。
如果上面的计算满足,就可以证明叠加定理了。
结论
在这个实验中,我们可以证明通过电阻的电流是连接单个能源时电流的代数和。并证明了叠加定理。
- 相关文章:基尔霍夫电流和电压定律 (KCL &KVL) |解决的例子
叠加定理的应用
- 叠加定理可用于交流和直流网络。
- 当独立来源的数量较多时,很容易找到网络的响应。
- 它通过单独计算每个能源的影响来帮助计算电流通过和元件两端的电压。在我们可以确定所有来源的元素的综合影响之后。
叠加定理的缺点
- 叠加定理不适用于只有依赖源的电路。它至少需要两个独立的来源。
- 这个定理只适用于由线性元素组成的网络。它不适用于二极管、晶体管等非线性元件。
- 我们不能用这个定理计算幂。由于功率与电压和电流的平方成正比,因此它变得非线性。
- 此定理不适用于电阻随电压和电流变化的情况。对于所有能源,电阻值必须保持不变。
- 这个定理只适用于双边元素。如果网络的响应取决于电流的方向,则该定理不适用。
相关电路分析教程:
- Tellegen 定理 - 求解示例和 MATLAB 仿真
- 克莱默规则计算器 - 电路的 2 和 3 方程系统
- 惠斯通电桥——电路、工作、推导和应用
- 电气和电子工程计算器
- 5000 多个电气和电子工程公式和方程式
工业技术


