Tellegen 定理 - 求解示例和 MATLAB 仿真
Tellegen 定理 - 带求解示例的分步指南
什么是泰勒根定理?
泰勒根定理 由荷兰电气工程师和发明家 Bernard D.H. Tellegen 出版 在 1952 年。该定理是网络分析中其他定理中最重要和最基本的定理。其他大多数定理都是从这个定理推导出来的。
泰勒根定理依赖于基尔霍夫定律。因此,该定理可以适用于遵循基尔霍夫定律的网络。该定理适用于具有线性或非线性、时变或非变、无源或有源元件的广泛网络。
泰勒根定理指出;
泰勒根定理的工作基于能量守恒定律原理。该定理用于化学和生物应用中,以发现物理网络的动态行为。在信号处理中,该定理用于设计滤波器。
- 相关文章:戴维宁定理。带有已解决示例的分步指南
数学方程
对于定理的一般分析,我们考虑在网络中给出“n”个元素。通过元件的瞬时电流为i1, i2, i3, ...., in。而该支路的瞬时电压为v1, v2, v3, ...., vn。
因此element-1的瞬时电流和电压分别为i1和v1。该元件消耗的瞬时功率(p1)为v1i1。
p 1 =v 1 我 1
element-2 的瞬时幂为 (p 2);
p 2 =v 2 我 2
同理,n th 的瞬时幂 元素是 (p n );
pn =vn in
根据泰勒根定理,所有瞬时功率之和为零。这意味着我们需要对所有瞬时功率 p1, p2, p3, ...., pn 求和。
p 1 + p 2 + p 3 + … + pn = 0
v 1 我 1+ v 2 我 2 + v 3 我 3 + … + vn in = 0
一般形式,我们可以将上面的等式写成第k th 分支;
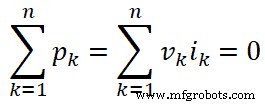
在哪里,
- n =网络中的分支总数
- vk =k th 的瞬时电压 分公司
- ik =k th 的瞬时电流 分公司
- pk =k th 的瞬时功率 分公司
现在,考虑下图分支AB等于分支k。

因此,瞬时电压vk;
vk =va – vb
而通过分支(a到b)的瞬时电流为ik;
ik =iab
所以,瞬时功率pk 是;
pk =vk ik =(va – vb) iab ……(1)
现在,我们考虑瞬时电流的反方向(b to a);
iab =– iab
瞬时电压;
vk =vb – va
瞬时功率pk 是;
pk =vk ik =(vb – va) iba ……(2)
等式1和2的求和;
2vk ik =(va – v b) i ab + (vb - va ) iba
vk ik =1/2 [(va – v b) i ab + (vb --va ) iba ] ….. (3)
对于n个分支,这个等式可以写成如下;
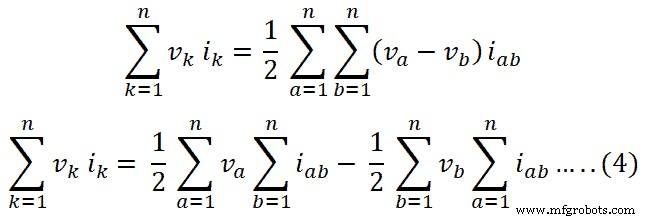
根据基尔霍夫电流定律,电流的代数和在电路的一个节点处为零。
因此,
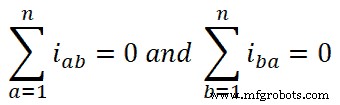
如果我们把这个值放在方程4中,我们得到;
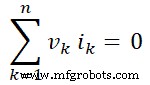
因此,证明传递给网络的功率总和为零。因此,证明了泰勒根定理。还描述了网络元素吸收的功率之和等于源提供的功率之和。
- 相关文章:诺顿定理。带有已解决示例的分步指南
Tellegen 定理的步骤
我们需要按照以下步骤通过 Tellegen 定理求解任何电网。
第一步: 我们需要在给定的电网中找到许多分支。然后找到每个分支的功耗。要找到功率,我们需要使用任何常规分析方法找到该分支的电压或电流。
第二步: 求每个分支的瞬时功率。
第三步: 具有能源的分支被视为电力输送分支。并且分支有其他元素被认为是一个能量吸收分支。现在确定供电支路和吸电支路。
第四步: 假设供电支路为正号,功率吸收支路为负压降。您也可以假设反向符号。但不能在整个示例中更改。
第五步: 为了证明 Tellegen 定理的合理性,我们需要添加从所有分支计算的所有功率。而且这个总和总是为零。
- 相关文章:SUPERMESH 电路分析 - 逐步解决示例
举个例子来理解吧。
Tellegen 定理求解示例
示例 #1
为以下网络证明 Tellegen 定理。
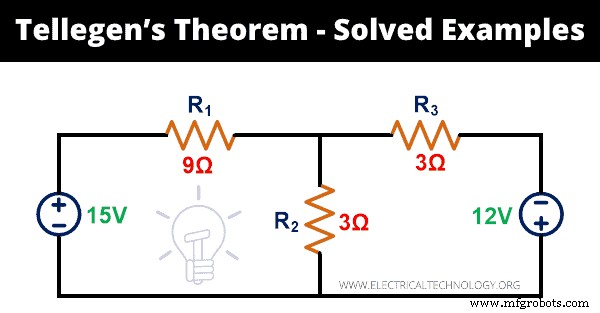
解决方案:
第一步: 给定的电路网络有 5 个分支。为了计算瞬时功率,我们需要找到通过每个分支的电流。为此,我们将 KVL 应用到网络中。
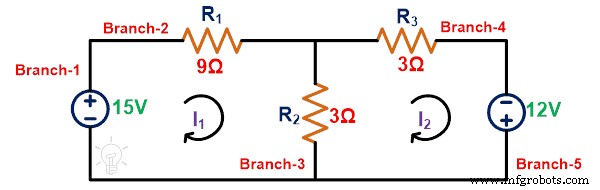
将KVL应用到loop-1;
15 =12I 1 – 3我 2
将KVL应用于loop-2;
12 =– 3I 2 + 6我 2
通过解上述方程,我们可以找到回路电流I1和I2的值。而这些值是;
我 1 =2A
我 2 =3A
第二步: 通过branch-3的电流为;
我 12 =我 2 - 我 1 =3 – 2 =1A
我们有电流流过所有分支。现在,找出每个分支的力量。
P 1 =V 我 1 =15 x 2 =30W
P 2 =R 1 我 1 2 =9 x 4 =36W
P 3 =R 1 我 12 2 =3 x 1 =3W
P 4 =R 3 我 2 2 =3 x 9 =27W
P 5 =V 我 2 =12 x 3 =36W
第三步: 有两个分支有来源。这三个分支是供电分支,其他三个分支是吸能分支。
这里,对于这个例子,我们假设供电支路的符号为正,功率吸收支路的符号为负。因此,支路1和支路5为供电支路,其他支路为吸电支路。
第四步: 电源P1、P5的符号为正(送电支路),P2、P3、P4的符号为负(吸电支路)。
第五步: 现在,我们需要找到所有分支耗散功率的总和。
P 1 - P 2 - P 3 - P 4 + P 5 =30W – 36W – 3W – 27W + 36W =0W
所以,瞬时功率之和为零。因此,这个定理被证明了。
- 相关文章:SUPERNODE 电路分析 - 逐步解决示例
示例 #2
使用 Tellegen 定理求 6A 电流源两端的电压。
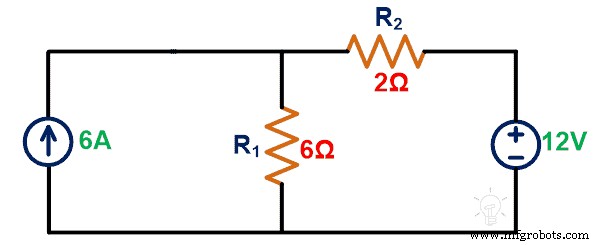
解决方案:
第一步: 我们需要计算通过元件的电压或电流。为此,我们将 KCL 或 KVL 应用于给定的网络。
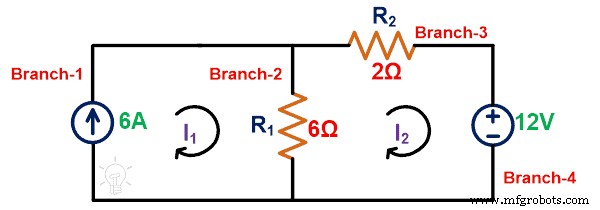
将KVL应用于loop-2;
-12 =8I 2 - 6我 1
电流通过分支的电流源为I 1;
我 1 =6A
把这个值代入上式;
-12 =8I 2 – 6(6)
-12 =8I 2 - 36
36 – 12 =8I 2
24 =8I 2
我 2 =3A
第二步: 流经支路2的电流为;
我 12 =我 1 - 我 2 =6 – 3 =3A
现在,找出每个分支的力量;
P 1 =V 我 1 =V x 6 =6 x V
P 2 =R 1 我 12 2 =6 x 9 =54W
P 4 =R 2 我 2 2 =2 x 9 =18W
P 4 =V 我 2 =-12 x 3 =-36W
第三步: 在这里,两个分支具有能源。因此,我们必须将这些分支视为电力输送分支。并将正号设置为瞬时功率。
另外两个分支只有电阻。所以,这些支路是吸能支路,负号为瞬时功率。
第四步: 功率 P1 和 P4 的符号为正,功率 P2 和 P3 的符号为负。
第五步: 现在,我们需要总结所有瞬时功率。
P 1 - P 2 - P 3 + P 4 =0W
P 1 – 54 – 18 + 36 =108W
6A电流源输出功率为108W。因此,电流源两端的电压由下式计算;
P 1 =V 我
108W =V x 6A
V =18V
因此,电流源两端的电压为18V。
- 相关文章: 交流和直流电路的最大功率传输定理
使用 MATLAB 分析和模拟 Tellegen 定理
目标:
证明上例给出的电路图的泰勒根定理。
要求: MATLAB
理论:
根据Tellegen定理,所有分支的求和瞬时幂等于0。为了证明这个定理,我们需要计算所有分支的瞬时功率。
要求瞬时功率,我们需要计算所有支路的电压或电流。为此,我们可以使用 KCL 或 KVL 定理。但这里我们将使用 MATLAB Simulink 模型来求电流和电压。
我们也可以使用其他软件,如multisim、psim等。我们将在Simulink模型中构建电路图。通过 Simulink 模型,您可以找到每个分支的电压和电流。
之后就可以从电压和电流求出瞬时功率了。您可以直接从一些软件中找到瞬时功率。
MATLAB Simulink 模型
下图为上例的电路图。
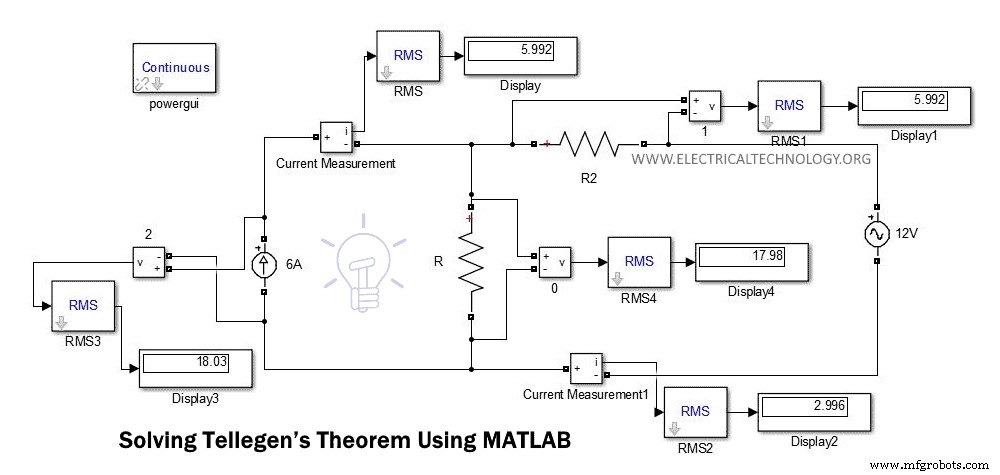
在这个图中,我们可以直接从显示器上找到电压和电流。您可以借助 KCL 或 KVL 通过计算电压和电流来比较这些值。
计算
计算电压或电流后,即可求出瞬时功率。或者您可以直接从软件中找到瞬时功率。我们所需要的只是瞬时功率。之后,我们需要添加所有的权力。
幂的总和总是为零。在本例中,我们比较了从 Simulink 中找到的电压和电流值,以及在上一个示例中使用 KVL 和 KCL 计算的相同值。这些值是相同的。
这些值也是由面包板上的连接电阻和源计算得出的。并且我们可以借助电压表和电流表测量流过所有支路的电压和电流。
因此,证明了泰勒根定理。
- 相关文章:基尔霍夫电流和电压定律 (KCL &KVL) |解决的例子
泰勒根定理的应用
这个定理非常基础,广泛用于电路分析。这个定理有很多应用。下面列出了一些应用程序。
- 对于滤波器的设计,这个定理在数字信号处理的应用中非常有用。
- 为了确定化工厂的稳定性,这个定理用于化学工程。
- 该定理适用于具有线性-非线性、主动-被动、时变/时不变元素的集总系统。
- 此定理用于生物过程。
- 用于拓扑结构反应分析。
- 也用于查找物理网络的动态行为。
相关电路分析教程:
- 叠加定理 - 带求解示例的电路分析
- 克莱默规则计算器 - 电路的 2 和 3 方程系统
- 惠斯通电桥——电路、工作、推导和应用
- 电气和电子工程计算器
- 5000 多个电气和电子工程公式和方程式
工业技术


