戴维南定理

戴维南定理指出，可以将任何线性电路（无论多么复杂）简化为仅具有单个电压源和连接到负载的串联电阻的等效电路。 “线性”的限定与叠加定理中的限定相同，其中所有基本方程必须是线性的（没有指数或根）。如果我们正在处理无源元件（例如电阻器，以及后来的电感器和电容器），这是正确的。然而，有些元件（尤其是某些气体放电元件和半导体元件）是非线性的：即它们对当前变化的反对 电压和/或电流。因此，我们将包含这些类型组件的电路称为非线性电路 .

电力系统中的戴维南定理

戴维南定理在分析电力系统和其他电路时特别有用，其中电路中的一个特定电阻器（称为“负载”电阻器）会发生变化，并且需要对每个负载电阻的试验值重新计算电路，以确定它两端的电压和通过它的电流。让我们再看看我们的示例电路：

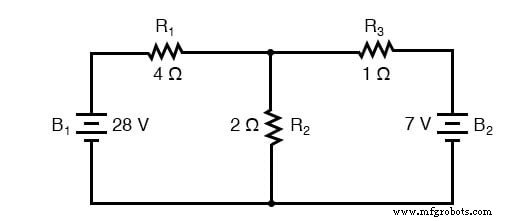
假设我们决定将 R2 指定为该电路中的“负载”电阻器。我们已经可以使用四种分析方法（分支电流、网格电流、米尔曼定理和叠加定理）来确定 R2 上的电压和通过 R2 的电流，但这些方法中的每一种都很耗时。想象一遍又一遍地重复这些方法中的任何一种，以找出如果负载电阻改变会发生什么（改变负载电阻非常 在电力系统中很常见，因为根据需要打开和关闭多个负载。它们的并联连接的总电阻根据一次连接的数量而变化）。这可能涉及很多 工作的！

戴维南等效电路

戴维南定理通过暂时从原始电路中去除负载电阻并减少由单个电压源和串联电阻组成的等效电路的剩余部分，使这变得容易。然后可以将负载电阻重新连接到这个“戴维南等效电路”并进行计算，就好像整个网络只不过是一个简单的串联电路：

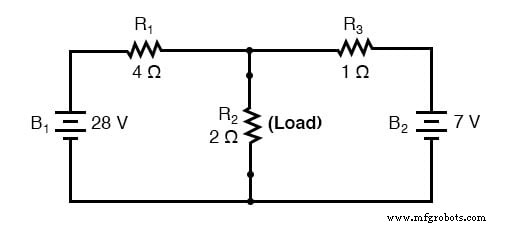
. . .戴维宁转换后。 . .

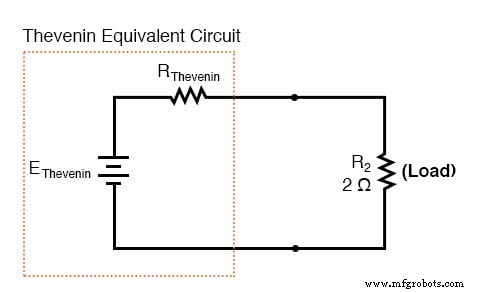
“戴维南等效电路”是 B1、R1、R3 和 B2 的电气等效电路，从我们的负载电阻 (R2) 连接的两个点来看。

如果推导正确，戴维南等效电路的行为将与由 B1、R1、R3 和 B2 形成的原始电路完全相同。换句话说，对于两个电路中相同的负载电阻值，负载电阻 (R2) 的电压和电流应该完全相同。负载电阻 R2 无法“分辨”B1、R1、R3 和 B2 的原始网络与 EThevenin 和 RThevenin 的戴维南等效电路之间的差异，前提是已经正确计算了 EThevenin 和 RThevenin 的值。

对更简单的电路执行“戴维南转换”的好处当然是它使负载电压和负载电流比原始网络更容易解决。计算等效戴维南源电压和串联电阻实际上很容易。首先，将选择的负载电阻从原电路中去掉，换上一个break（开路）：

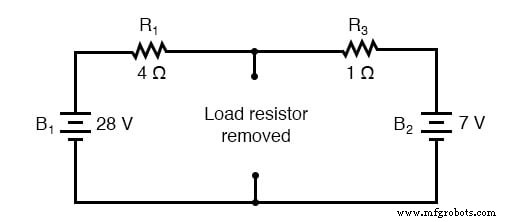
确定戴维宁电压

接下来，确定用于连接负载电阻的两点之间的电压。使用您可以使用的任何分析方法来执行此操作。在这种情况下，去掉负载电阻的原始电路只不过是一个带有相反电池的简单串联电路，因此我们可以通过应用串联电路规则、欧姆定律和基尔霍夫电压来确定开路负载端子上的电压法律：

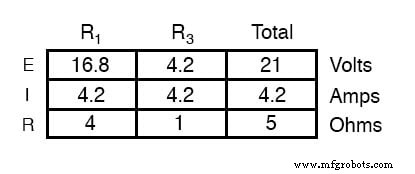
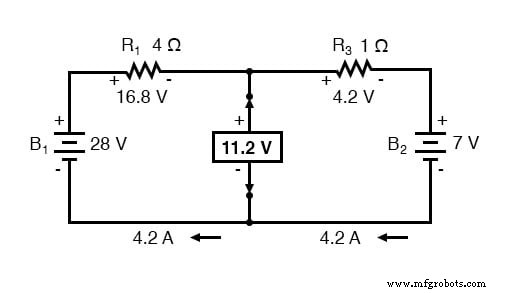
两个负载连接点之间的电压可以从电池电压之一和电阻器之一的电压下降得出 11.2 伏。这是我们等效电路中的“戴维宁电压”（EThevenin）：

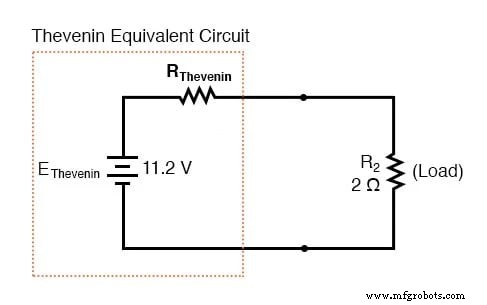
确定戴维宁串联电阻

为了找到我们等效电路的戴维南串联电阻，我们需要采用原始电路（负载电阻仍被移除），移除电源（与我们对叠加定理所做的相同：电压源被电线和电流源替换为断点），并计算从一个负载端子到另一个的电阻：

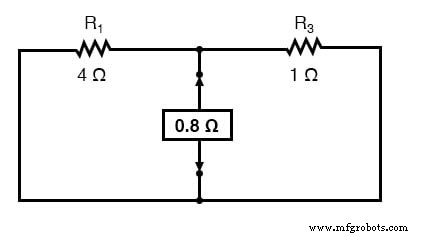
移除两个电池后，在该位置测得的总电阻等于并联的 R1 和 R3：0.8 Ω。这是我们用于等效电路的“戴维宁电阻”（RThevenin）：

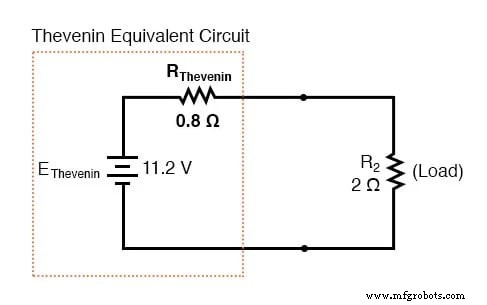
确定负载电阻两端的电压

通过在连接点之间连接负载电阻 (2 Ω)，我们可以确定它两端的电压和通过它的电流，就好像整个网络只不过是一个简单的串联电路：

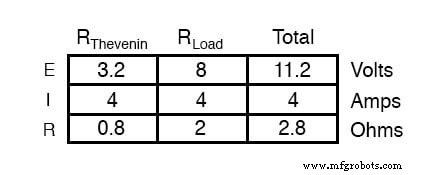
请注意，R2（8 伏，4 安）的电压和电流值与使用其他分析方法得出的值相同。还要注意戴维宁串联电阻和戴维宁源的电压和电流值（总 ) 不适用于原始复杂电路中的任何组件。戴维宁定理仅用于确定 单个 网络中的电阻：负载。

当然，优点是您可以快速确定如果单个电阻的值不是 2 Ω 会发生什么情况，而无需再次进行大量分析。只需将负载电阻的另一个值插入戴维南等效电路中，稍加串联电路计算即可得出结果。

评论：

• 戴维南定理是一种将网络简化为由单个电压源、串联电阻和串联负载组成的等效电路的方法。
• 戴维宁定理的步骤：
  • 通过从原始电路中移除负载电阻并计算负载电阻原来所在的开路连接点上的电压，找到戴维宁电源电压。
  • 通过移除原始电路中的所有电源（电压源短路和电流源开路）并计算开路连接点之间的总电阻，找到戴维南电阻。
  • 画出戴维南等效电路，戴维南电压源与戴维南电阻串联。负载电阻重新连接在等效电路的两个开路点之间。
  • 按照串联电路的规则分析负载电阻的电压和电流。

相关工作表：

• 戴维南、诺顿和最大功率传输定理工作表