EasyFFT：Arduino 的快速傅立叶变换 (FFT)

应用和在线服务

Arduino IDE

关于这个项目

从捕获的信号中测量频率可能是一项艰巨的任务，尤其是在 Arduino 上，因为它的计算能力较低。有一些方法可用于捕获零交叉，其中通过检查信号在给定时间内穿过零线的次数来捕获频率。当信号是各种频率的组合时，这种方法可能不起作用。

如果您不是来自这样的背景，这在某种程度上很难编码。但作为修补匠，此代码可能对与音乐、信号分析相关的各种项目非常有用。该项目的动机是编写一个代码，无需深入了解它的背景，即可轻松在 Arduino 上实现。

本项目不解释 FFT 的工作原理，而是解释 FFT 函数的应用。所附视频中也解释了相同的过程。

如果您只对代码的应用感兴趣，而不是对其进行解释。您可以直接跳到第 3 步。

如果您需要以高速 (3x) 执行 FFT，同时精度略有妥协（约 5%），请参阅我关于 ApproxFFT 的另一篇文章。

https://create.arduino.cc/projecthub/abhilashpatel121/approxfft-fastest-fft-function-for-arduino-fd4917?ref=user&ref_id=1593632&offset=0

第 1 步：快速傅立叶变换

为了使 DFT 的计算更快，James Cooley 和 John Tukey 开发了 FFT 算法。该算法也被认为是20世纪最重要的算法之一。它将信号分为奇数和偶数序列部分，从而降低了所需的计算数量。通过使用它，总需要的复数乘法可以减少到 NlogN。这是一个显着的改进。典型的 DFT 需要 N*N 的复数乘法才能得到结果，而 FFT 只需要 N*logN。当样本数量较多时，这是一个显着的优势。

您可以参考以下我在编写代码时参考的参考资料，以详细了解 FFT 背后的数学原理：

1. https://flylib.com/books/en/2.729.1/derivation_of_...

2. https://jakevdp.github.io/blog/2013/08/28/understa...

3. https://cnx.org/contents/[email protected]:zmcmahhR@7/D...

4. https://en.wikipedia.org/wiki/Fast_Fourier_transfo...

第二步：代码说明

1. 快速正弦和余弦：

计算 FFT 多次取各种正弦和余弦的值。 Arduino 的内置功能不够快，需要很长时间才能提供所需的值。这使得代码显着变慢（64 个样本的时间加倍）。为了解决这个问题，0 到 90 度的正弦值存储为 255 的倍数。这样做将消除将数字存储为浮点数的需要，我们可以将其存储为字节，占用 Arduino 上的 1/4 空间。 sine_data[ ] 需要粘贴在代码顶部以将其声明为全局变量。

除了 sine_data 之外，还有一个名为 f_peaks[] 的数组声明为全局变量 .每次运行 FFT 函数后，此数组都会更新。其中 f_peaks[0] 是最主要的频率，其他值按降序排列。

byte sine_data [91]={0, 4, 9, 13, 18, 22, 27, 31, 35, 40, 44, 49, 53, 57, 62, 66, 70, 75, 79 , 83, 87, 91, 96, 100, 104, 108, 112, 116, 120, 124, 127, 131, 135, 139, 143, 146, 150, 153, 6, 15, 15 17 17 , 177, 180, 183, 186, 189, 192, 195, 198, 201, 204, 206, 209, 211, 214, 216, 219, 221, 223, 2, 2, 2, 2, 2, 3, 2, 3, 2, 3, 3 , 238, 240, 241, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 253, 254, 254, 254, 254, 245, 246, 247, 248, 249, 250, 251, 252, 253, 253, 254, 254, 254, }5,5, 5 _ 5 s 浮点数]; 

由于我们存储了 0 到 90 度的正弦值，因此可以计算任何正弦或余弦值。下面函数将数字的第一轮到小数点为零并从存储的数据中返回值。这种方法只需要一个浮动除法。这可以通过直接存储正弦值（不是 255 倍数）来进一步减少。但这会占用 Arduino 的大量内存。

使用上述过程会降低准确性，但会提高速度。 64分有8ms的优势，128分有20ms的优势。

第三步：代码说明：FFT函数

FFT 只能对 2、4、8、16、32、64 等样本大小进行。如果值不是 2^n，则取值的下侧。例如，如果我们选择样本量为 70，则它只会考虑前 64 个样本，而忽略其余部分。

始终建议样本大小为 2^n。可以是：

2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048,...

两个浮点数 out_r 和 out_im 将占用大量内存。由于缺乏可用内存，Arduino nano 不适用于高于 128（在某些情况下为 128）的样本。

unsigned int data[13]={1,2,4,8,16,32,64,128,256,512,1024,2048};int a,c1,f,o,x;a=N; for(int i=0;i<12;i++) //计算水平 { if(data[i]<=a){o=i;} } int in_ps[data[o]]={}; //排序的输入float out_r[data[o]]={}; //transformfloat的实部 out_im[data[o]]={}; //变换的虚部 

进一步的流程如下：

1. 代码为给定的样本大小生成位反转的顺序（参考文献中位反转的详细信息：步骤 2）

2.输入数据按生成顺序排序，

3. FFT 执行

4.计算复数的幅度，

5. 检测峰并按降序排列

6.结果可以从f_peaks[]获取。

[访问其他数据（峰值频率除外）的代码应该修改，以便可以将局部变量复制到某个预定义的全局变量]

第 4 步：测试代码

给出一个样本三角波作为输入。由于该波的采样频率为10Hz，波本身的频率为1.25Hz。

从原始输出可以看出，值与 Scilab 计算的 FFT 匹配。然而，这些值与我们低精度但更快的正弦波并不完全相同。

输出频率阵列频率分别为1.25和3.75。没有必要每次都获得准确的值。通常这些数字被称为频率仓。所以输出值可能在指定区间内的任何地方。

速度：

对于 Arduino nano，它需要：

• 16 分：4 毫秒

• 32 点：10 毫秒

• 64 点：26 毫秒

• 128 点：53 毫秒

第 5 步：结论

该 FFT 代码可用于实时应用。因为完成计算需要大约 30 毫秒。但是，它的分辨率受到样本数量的限制。样本数量受 Arduino 内存限制。通过使用 Arduino Mega 或其他更高性能的板卡可以提高精度。

如果您有任何疑问、建议或更正，请随时发表评论。

代码

• EasyFFT

EasyFFTArduino

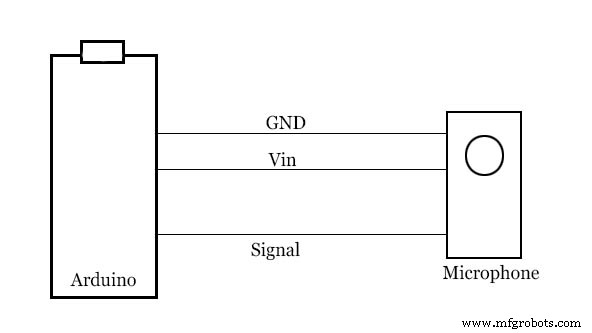
/*//Example data:int data[64]={14, 30, 35, 34, 34, 40, 46, 45, 30 , 4, -26, -48, -55, -49, -37,-28, -24, -22, -13, 6, 32, 55, 65, 57, 38, 17, 1, -6, - 11, -19, -34, -51, -61, -56, -35, -7, 18, 32, 35, 34, 35, 41, 46, 43, 26, -2, -31, -50, -55, -47, -35, -27, -24, -21, -10, 11, 37, 58, 64, 55, 34, 13, -1, -7};*///---- -------------------------------------------------- ---------------------//byte sine_data [91]={0, 4, 9, 13, 18, 22, 27, 31, 35, 40, 44, 49, 53, 57, 62, 66, 70, 75, 79, 83, 87, 91, 96, 100, 104, 108, 112, 116, 120, 124, 127, 13,31, 4 146, 150, 153, 157, 160, 164, 167, 171, 174, 177, 180, 183, 186, 189, 192, 195, //粘贴在程序顶部198, 20, 120, 198, 201, 120 、214、216、219、221、223、225、227、229、231、233、235、236、238、240、241、243、244、245、245、245、246、246 , 253, 253, 254, 254, 254, 255, 255, 255, 255 };float f_peaks[5]; // 按降序排列的前 5 个频率峰值//-------------------------------------- ------------------------------------//void setup() { Serial.begin(250000); } void loop() {////exampleFFT(data,64,100); //在 100Hz 时获得 64 个样本的 X 频率的前五个值。 )，可用频率 f_peaks[0],f_peaks[1],f_peaks[2],f_peaks[3],f_peaks[4],*/ }//--------------- --------------FFT 功能-------------------- ------------//float FFT(int in[],int N,float Frequency){/*在arduino上执行FFT的代码，设置：在程序顶部粘贴sine_data [91]全局变量]，在程序末尾粘贴 FFT 函数Term:1。 in[] :数据数组, 2. N :样本数（推荐样本大小 2,4,8,16,32,64,128...）3。频率：输入所需的采样频率（Hz）如果样本大小不是 2 的幂，它将被剪裁到数字的较低侧。即，对于 150 个样本，代码将考虑前 128 个样本，其余样本将被省略。对于 Arduino nano，由于 mamory 限制，无法进行超过 128 个样本的 FFT（推荐 64）对于更高的样本数可能会出现与 Mamory 相关的问题，ABHILASHContact 的代码：[email protected] 文档：https://www.instructables.com/member/abhilash_patel/instructables/2/3/2021：将 N 的数据类型从 float 更改为 int 以获取>=256 个样本* /unsigned int data[13]={1,2,4,8,16,32,64,128,256,512,1024,2048};int a,c1,f,o,x;a=N; for(int i=0;i<12;i++) //计算水平 { if(data[i]<=a){o=i;} } int in_ps[data[o]]={}; //排序的输入float out_r[data[o]]={}; //transformfloat的实部 out_im[data[o]]={}; //变换的虚部x=0; for(int b=0;ba) {out_r[i]=in[in_ps[i]-a];} }int i10,i11,n1;float e,c,s,tr,ti; for(int i=0;i 这里向前 out_r 包含振幅，our_in 包含频率 (Hz) for(int i=0;iout_r[i-1] &&out_r[i]>out_r[i+1] ) {in_ps[x]=i; //in_ps 数组用于存储峰值数 x=x+1;} }s=0;c=0; for(int i=0;i360){j=j-360;} if(j>-1 &&j<91){out=sine_data[j];} else if (j>90 &&j<181){out=sine_data[180-j];} else if(j>180 &&j<271){out=-sine_data[j-180];} else if(j>270 &&j<361){out=-sine_data[360-j];} return (out/255);}float cosine(int i){ int j=i;浮出水面； while(j<0){j=j+360;} while(j>360){j=j-360;} if(j>-1 &&j<91){out=sine_data[90-j];} else if(j>90 &&j<181){out=-sine_data[j-90];} else if(j>180 &&j<271){out=-sine_data[270-j];} else if(j>270 &&j<361){out=sine_data[j-270];} return (out/255);}//---------------------- -------------------------------------------------- ------------//

示意图