纳米团簇的神奇数学关系

介绍

纳米团簇的幻数和公式有着悠久的历史，可以追溯到 1969 年由 van Hardeveld 和 Hartog 发表的有先见之明的出版物 [1]。他们的见解早于纳米科学时代。从那以后，我们看到幻数出现在 2D 多边形和 3D 多面体 [2]、碳富勒烯 [3] 中，并再次出现在有限范围内的簇 [4]。诸如硅 [5]、硼 [6] 之类的多样化材料，事实上，来自索引服务“Web of Science”的 1000 多篇出版物都引用了簇中的幻数。研究纳米团簇的大小和形状对当今社会很重要，因为这不仅决定了其固有的物理和化学性质，还决定了其与光学、催化、电子和磁性应用的相关性 [7]。我们的目标是用当前的关系和数据更新这些知识的数据库，现在我们已经进入了纳米领域。

纳米团簇中幻数的出现主要与基本细胞上原子壳的形成有关。当原子的数量构成一个完整的壳时，我们会发现一组独特的数字，称为“魔法”，它定义了原子的壳。簇由以原子为顶点、以键为边的图表示。它由嵌套的壳组成，如洋葱层。我们将层数定义为 n 并发现最近邻配位数、键、原子总数和一些拓扑指数的数学关系作为 n 的函数 . van Hardeveld 和 Hartog [1] 的原始论文考虑了 fcc、bcc 和 hcp 集群。 Teo 和 Sloane [2] 的参考文献考虑了多面体和柏拉图立体，但忽略了最近邻配位数的关系。我们通过查看简单立方体、金刚石立方体和柏拉图固体，以及簇的拓扑特性和色散来添加到这个数据库中。

从体块到几个原子簇的大小转变实际上是关于表面原子与体原子之间的关系。催化化学、表面等离子体共振和光学量子点光致发光等特性 [8] 受表面原子的配位和数量的影响。表面原子的分散或相对百分比是由表面原子与原子总数的比率决定的，如前所述[9]。我们的分析将确定离散在簇几何方面的相对排名。

拓扑指数始于 Wiener 关于他的指数和石蜡沸点的原始论文 [10]。直到一段时间后，Hosoya 才引入了一种数学形式来分析拓扑指数 [11]。我们之前已经介绍了拓扑指数和纳米团簇 [12]。在撰写本文时，存在许多索引，其中一些依赖于邻接矩阵或距离矩阵。我们在这里表明，在许多簇形状中，四个指数存在神奇的数学关系，作为 n 的函数 和炮弹数。

方法

对于我们研究的每种类型的簇，我们创建了一个计算算法来确定簇的原子坐标。然后我们继续创建一个邻接矩阵和一个距离矩阵，定义如下。邻接矩阵A 在我们定义 i 的地方创建 和 j 作为最近的邻居，并通过要求 r ij <r c , 其中 r c 是一个阈值，略高于最近邻距离，但小于第二邻距离。因此，

其中 r ij 是原子 i 之间的欧几里得距离 和原子 j . r 的适当值 c 是 1.32·r 分钟 , 其中 r 分钟 是最小的键长。这适用于十二面体结构，以及我们研究的其他结构。集群的协调数只是邻接矩阵的一列中非零元素的数量。距离矩阵定义为

$$ \mathbf{D}(i,j) =\left\{\begin{array}{ll} 0 &i =j \\ d_{ij} &i \neq j \end{array}\right。 $$ (2)

其中 d ij 是图中从 i 开始的最短路径的长度 j .存在从邻接矩阵计算距离矩阵的有效算法[13]。使用这些定义，我们可以计算维纳指数，W (G )，超维纳指数，W W (G )，逆维纳指数rW (G ) 和 Szeged 指数 Sz (G )，如前所述[14]。这些计算使用的算法与我们之前用于拓扑指数和纳米团簇的算法相同[12]。

以前的作者提供了魔法关系的证明，我们将其浓缩在我们的符号中，与此处介绍的工作相关 [1, 2]。由于我们创建了最近邻邻接矩阵，我们知道配位数 c n 我 顶点 i 通过对 A 的元素求和 (i ,:)。我们的结构由 n 组成 +1 炮弹编号为 0,1,...,n .令\(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\) 是配位c的原子数 n 我 其中 1≤c n 我 ≤c n M 与 c n M 集群中的最大协调。那么簇中的原子总数由

给出 $$ N_{T}(n) =\sum_{{cn}_{i}=1}^{{cn}_{M}}{N_{{cn}_{i}}(n)}。 $$ (3)

外壳中的表面原子 n 具有一组小于体配位的键。因此，表面原子的最大配位是 c n s <c n M , 表面原子数为

$$ N_{S}(n) =\sum_{{cn}_{i}=1}^{{cn}_{s}}{N_{{cn}_{i}}(n)}。 $$ (4)

如果所有非表面顶点的坐标都大于 c n s ，这适用于所有簇，但请注意下面十二面体的差异。我们通过计算和为 c 的邻接矩阵的列来确定 \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\) n 我 .请注意，我们的聚类坐标算法是由壳层构建的，因此每个后续壳层都包含 n 的所有先前较低值 .在图 1 中，我们说明了 fcc 立方体和十二面体的簇壳。此外，簇中的键数为

$$ N_{B}(n) =\frac{1}{2}\sum_{{cn}_{i}=1}^{{cn}_{M}}{{cn}_{i}\ cdot N_{{cn}_{i}}(n)}, $$ (5)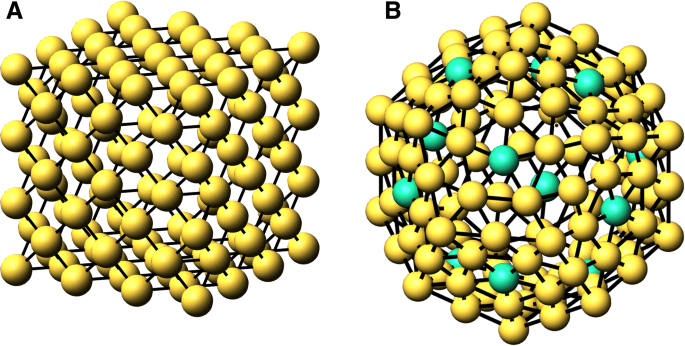

n 的原子壳 =3 对于 A. fcc 立方体和 n =2 B.十二面体。在 B 中，绿色原子 (12) 指的是 c n =5 内壳

其中 N B (n ) 是债券的数量，c n M 是最大的协调。 1/2 的因子是由于成对最近邻键合而产生的。这种神奇的关系在以前的出版物中似乎没有被考虑过，除了 [4] 中检查的几个集群。我们还评论说，Teo 和 Sloane 推导出簇的原子总数、表面原子数和内部原子数如下[2]：

$$ N_{T}(n) =\alpha n^{3}+\frac{1}{2}\beta n^{2}+\gamma n+1~~n\ge{0} $$ ( 6)

其中 N T (n ) 是原子总数，而

$$ \alpha =C/6 $$ (7)

其中 C 是多面体被划分成的四面体单元的数量，并且

$$ \beta =1/2F_{s} $$ (8)

其中 F s 是曲面上三角形面的数量，而

$$ \gamma =F_{s}/4+V_{i}+1-C/6 $$ (9)

其中 V 我 是内部的顶点数。他们还表明

$$ N_{S}(n) =\beta n^{2}+2~~n\ge{1};~~N_{S}(0) =1 $$ (10)

和

$$ N_{I}(n) =N_{T}(n) - N_{S}(n), $$ (11)

其中 N 我 (n ) 是内部原子的数量。该信息（等式（11））包含在邻接矩阵中，以及等式。 （3、4、5）。这些方程是对邻接矩阵数据结果的检查。对于中心多面体，我们也有

$$ N_{I}(n) =N_{T}(n-1), $$ (12)

和从方程。 (11)，我们有

$$ N_{T}(n)=N_{S}(n)+N_{S}(n-1)+... +N_{S}(1)+N_{S}(0)。 $$ (13)

从这些方程中，我们可以推导出每个集群的神奇公式如下。计算拓扑(0,1)-邻接矩阵A后 对于具有 n 的集群 如所描述的贝壳，我们知道它的大小 N =N T (n ) 表示原子总数。 i 列中条目的总和 给出键数 c n 我 (n ) 对于原子 i 并计算等于 c 的列和的数量 n 我 (n ) 显然给出了 \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\)。因为我们知道这些依赖于 n 作为最多为 3 次的多项式，我们可以计算 N T (n ) 和 c n 我 (n ) 对于 n 的 4 个连续值 ，说 n =n 0+j , j =0,1,2,3。一个简单的内插多项式将给出多项式系数。必须验证通过增加 n 0，通常等于 1，公式不变。如果公式从 n 开始稳定 0 上，然后他们保持所有 n ≥n 0. 在某些情况下，多项式关系只对偶数 n 成立 值或奇数。例如，对于 fcc 菱形十二面体（表 1），当 n 时，连续的壳有八个配位为 3 的原子 ≥2 是偶数，如果 n 则没有 很奇怪。在这种情况下，不同的多项式关系将适用于 n 偶数和n 奇数，但数据用于 n =n 0+j , j =0,2,4,6 与 n 0 奇数（例如，n 0=1) 或 n 0 偶数 (n 0=2）。为了得到精确的有理系数，需要使用 MATLAB 的符号工具箱在精确算法中求解 Vandermonde 系统的系数。这就是表 2、3、4、5、1、6、7、8、9、10、11、12、13、14、15、16、17、18 和 19 的计算方式。在下一节中，我们确定 N 的魔法公式 T (n ), N B (n )，对于 \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\) 根据禁止的配方。

表面原子的色散（暴露的分数，FE）定义为：

$$ \text{FE} =\frac{N_{S}}{N_{T}} \cdot 100\% $$ (14)

其中 N S 是表面原子数，N T 是原子总数[9]。我们可以通过定义相对集群大小来比较不同的集群：

$$ d_{rel} =b(N_{T})^{1/3};~~b =d_{at}^{-1}\cdot \left(\frac{6V_{u}}{\pi n_{u}}\right)^{1/3} $$ (15)

其中 d 在 是共价原子直径，V 你 是晶胞的体积，n 你 是晶胞中的原子数。晶体结构常数b fcc 和 hcp 簇为 1.105，bcc 簇 [1] 为 1.137，简单立方簇为 1.488，金刚石立方簇为 1.517。如上所示，FE 的公式是聚类的二次方与三次方的比率，可以通过幂律曲线拟合与 d 进行建模 相对 .变量 d 相对 允许我们在不考虑晶体结构的情况下将不同的簇相互比较。对于一些没有晶胞的柏拉图星团，我们使用\(N_{T}^{1/3}\)作为变量。

结果与讨论

金属纳米团簇的大小和形状的研究从二十年前的起步阶段就开始发展。表 20 显示了截至 2018 年的一些相关进展。

在表中，我们主要列出了过渡金属，而不是合金或化合物，但截断的六边形双锥除外，其中仅发现了 Fe2O3。由于其性质和稳定性，金簇的合成比任何其他元素都要多。在接下来的小节中，我们将讨论限制在与魔法公式和聚类类型相关的特定主题上。

FCC 集群

八种过渡金属在 fcc 结构中结晶，参见下表 21，包括等离子体贵金属和重要的催化活性元素。绝大多数纳米团簇合成都是用这些元素进行的。表21给出了各种形状和尺寸的fcc元件的合成参考。

这些元素的合金也很有趣，但这些元素的参考文献太多，无法在此引用。通常，合成的常见形状是立方体、八面体、立方八面体和二十面体。通常，具有（111）面的簇更容易合成，因为（111）面的能量通常低于（100）面[7]。我们发现 fcc 菱形十二面体存在偶数和奇数公式。这些与 [1] 中的一致，如果将“n ” 在我们的偶数公式中乘以 2(m -1). [24] 中列出的 fcc 立方八面体的公式产生与我们相同的幻数，但由于它们将壳编号为 n，因此移位了 1 =1,2,... 我们使用编号 n =0,1,....我们的魔法公式与 [2, 4] 中的那些一致，并尊重早期发表的工作，并保持数学的连续性，我们使用 [2, 4] 符号。 5 个 fcc 簇形状及其相关的魔术公式如下所示。

BCC 集群

元素周期表中的七种过渡金属具有 bcc 结构，见表 21。在磁性元素 Fe、Co 和 Ni 中，只有铁是 bcc 结构。铁纳米立方体似乎是迄今为止合成的唯一 bcc 簇形状 [25]。尽管铁的整体结构是体心立方，但已经合成了面心立方纳米团簇 [26]。该参考文献还分析了团簇的热力学稳定性。在这里，我们展示了 5 个 bcc 簇形状及其相关的魔法公式。

HCP 集群

十二种过渡金属具有 hcp 结构，参见表 21。然而，其中许多会氧化，或缺乏令人信服的科学兴趣来合成。关于表 11 中的六边形双锥簇形状，已经合成了金簇 [27]。相关的截头六边形双锥似乎仅由 α 形成 −Fe2O3 [28]。

柏拉图集群

柏拉图固体自古希腊人就已为人所知。它们包括立方体、四面体、八面体、二十面体和十二面体。在前面的表格中，我们列出了 fcc 和 bcc 立方体和八面体的神奇公式。这里我们列出了二十面体、十二面体、四面体和体心四面体的公式。正如前面在“方法”部分提到的，十二面体对于这里分析的簇来说是独一无二的，因为 c n s =7 指的是表面原子和体原子。我们在图 1b 中展示了外壳包含五重和六重配位原子。当壳变成内部时，那些五重和六重配位的原子变成七重和八重配位，并与任一侧的壳键合。此外，六重配位的壳外原子通过键合到壳内而实现七重配位。因此，十二面体有七重表面和体配位原子。结构中的每个壳有 12 个五重壳原子，产生 12n -12 块体七重配位原子。其余的七重配位是表面原子。

金纳米团簇已被证明具有柏拉图的形状 [29]。此参考包括立方体、四面体、八面体和二十面体。后来又合成了金十二面体纳米团簇[30]。在这里，我们展示了正四面体，它在 c 中是“类似 fcc”的 M =12 如 fcc 结构，以及表 16 中的体心四面体，其中绿色原子具有单键。柏拉图魔术公式如下所示。

菱形立方、简单立方和十面体簇

元素硅和锗具有金刚石立方晶格，以及碳的金刚石同素异形体。特别是，氢封端的硅最近受到了关注。 (100) 氢终止表面，导致立方体形状的簇，已被确定具有最低的能量 [31]。已经实现了尺寸为 8-15 nm 的 Si-H 纳米立方体的合成 [32]。表 17 显示了氢封端的 Si-H 簇的示意图，绿色的单键氢原子。如果纳米团簇呈菱形立方体，则会有单个悬空键，需要对其进行钝化以帮助维持结构。看看神奇的公式，我们建议这种 Si-H 簇的组成是 \(\phantom {\dot {i}\!}\text {Si}_{8n^{3}+6n^{2}-9n +5}\text {H}_{12n-8}\)，其中 n 是集群中的外壳数量。这种半导体量子点可能对光学特性感兴趣，并且带隙随氢端基团簇大小的变化已被确定与簇大小成反比[33]。

简单的立方晶格结构之前已经被其他人分析过 [4]，尽管我们没有提供细节。我们之前研究过 d 维超立方体形式 [14]。钋是唯一具有简单立方结构的元素。它是放射性的，可能会导致专门的应用。这里我们介绍菱形立方、简单立方和十面体簇魔术公式。

神奇的拓扑公式

测量晶体中的结构复杂性可以让我们了解结构的简单性或复杂性，正确使用可以对相关结构进行排序。对于此类排名，考虑晶格的图形描述是有帮助的，如“方法”部分所述。晶体结构的拓扑复杂度由图的顶点度分布来衡量，I vd [34]，使用软件ToposPro，版本5.3.2.2 [35]：

其中 a 我 是 i 的度数（坐标） 第一个顶点和求和沿着所有 v 进行 商图的顶点。该参数使用无限晶体，而不是我们一直在考虑的簇，但对于测量不同晶体结构的相对复杂性很有用。因此，数字越大，或者图中的信息内容越多，它就越复杂。在表 22 中，我们显示了 I 的值 vd 从来自晶体学开放数据库中晶体结构的 cif 文件的 ToposPro 中获得。钋是唯一在简单立方结构中结晶的元素，其值为零，即商图有一个顶点和零边，与我们所期望的一致，简单立方结构确实是最不复杂的结构。还显示了盐，NaCl，具有简单立方结构中的两种元素，以及金刚石立方结构中的硅、fcc 中的金、bcc 中的铁和 hcp 结构中的钴。我们提到与香农熵 [34] 相关的另一个复杂性度量没有用，因为所有元素的这个度量都相同。

可以将与“方法”部分中描述的确定魔术公式的方法类似的方法应用于描述拓扑索引的魔术公式。只有在这里，多项式的次数是 7、8 或 9，因此它们的值至少为 10 个连续的 n -需要计算值。然后更高阶的插值问题给出结果。由于用符号工具箱求解一个大小为 10×10 的线性系统需要一些时间，因此可以使用多个右侧同时计算拓扑索引的所有系数，以获得所有多项式的系数。

拓扑指数的魔术公式在表 23、24 和 25 中详述。我们分析的四个指数仅取决于 n ，集群中的 shell 数量。从结果来看，简单立方晶格作为最不复杂的结构，也有“最简单”的公式。尽管我们付出了努力，我们还是无法解出 bcc 立方体的 Szeged 指数。没有找到稳定的解决方案。一般来说，fcc 结构更容易求解拓扑公式。我们无法解决任何 hcp 结构，只能解决几个 bcc 结构。这可能与拓扑复杂性有关，因为 fcc 晶格比 bcc 或 hcp 更简单，请参见表 22。在表中，我们提供了立方八面体、二十面体和十面体的公式。我们之前 [12] 为这些指数提供了数值数据表，但需要注意的是 [12] 中的立方八面体具有不同的幻数。在这里我们看到，表格数据可以简洁地概括为神奇的公式。指数多项式的次数也遵循 3D 空间的规则 [14]。柏拉图固体的一些拓扑指数先前已发表[36]。从这个参考文献中，我们验证了 n 的所有五个固体的维纳指数 =1。已经研究了 fcc 晶格的晶胞行的 Wiener 指数 [37]，但由于我们研究了簇，因此无法比较我们的结果。

分散

各种簇的表面原子（分散，FE）百分比如图 2 所示。已知铂纳米簇对氧还原反应 (ORR) 具有催化活性，而氧还原反应 (ORR) 取决于大小和形状 [38]。该参考文献确定大小为 2.2 nm 的铂立方八面体簇具有最大的 ORR 活性。众所周知，对于 PtNi 合金，(111) 表面更适合 ORR [39]。我们在 d 比较了 FE 的二十面体、八面体、十面体和立方八面体簇 相对 =7.5 铂在 2.2 nm。二十面体、八面体和十面体簇具有带 (111) 面的表面。使用图 2 中的幂律，我们发现对于给定的 d 相对 二十面体簇的 FE 为 47.9%，立方八面体为 52.8%，十面体为 57.5%，八面体簇的 FE=58.9% .因此，基于形状，八面体簇具有 (111) 表面和相似尺寸的最高 FE 值。幂律系数和指数都与确定小 d 的有限元有关 相对 .幂律指数的数学解释给出了物理意义，即纵坐标 FE 与横坐标 d 的关系 相对 , 或 FE 的相对百分比变化与 d 的相对百分比变化 相对 .幂律系数只是当 d 时 FE 的值 相对 =1.

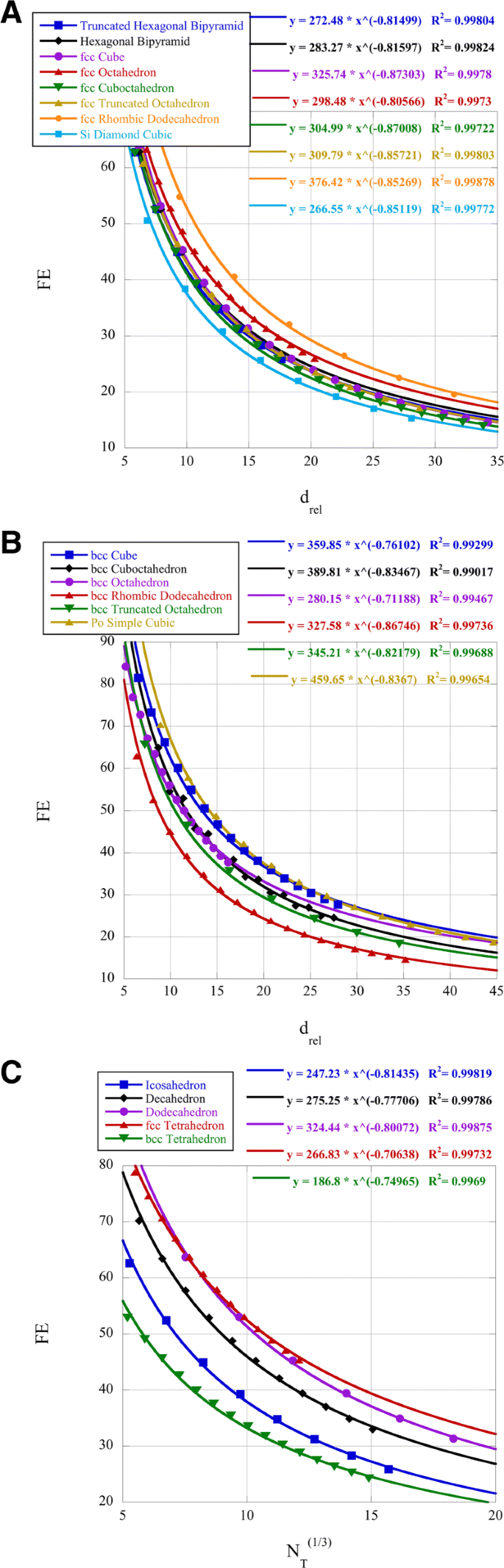
纳米团簇的分散有限元

另一个研究小组合成了铂合金二十面体簇，并将其活性与八面体簇进行了比较[40]。这些纳米团簇的大小约为 13 nm 或 N =20,000 八面体簇和 N =15,000 对于二十面体簇。这会产生 d 相对 =30 八面体簇和 25 二十面体簇。使用相关的幂律，这给出 FE=18.0% 对于八面体和 19.8% 对于二十面体簇。对于这种大小的簇，FE 的差异很小，但是由于孪晶，二十面体簇具有显着的应变，这可能会移动 d 波段中心，从而影响 ORR 结果 [40]。然而，考虑到 [38] 的大小相关数据，可能会建议较小的集群会产生更高的 ORR 数据。事实上，4 nm Pt3Ni 八面体在掺杂 Mo 时产生了创纪录的 ORR 结果 [41]。

结论

我们研究了 19 种类型的纳米团簇和一些有关原子数、键数、配位数和拓扑指数的神奇公式。这些包括 fcc、bcc、hcp、柏拉图固体、金刚石立方体、简单立方体和十面体簇。这些结果中的大多数比先前确定的更详细，并且第一次列举了大量结果。材料相关研究的一个宏伟目标是结构与特性的相关性。这项对纳米团簇神奇关系的详细研究是朝这个方向迈出的一步。一个例子是讨论表面原子的分散及其与催化活性的关系。我们希望这些结果将有助于科学家们对纳米团簇结构及其相关特性的研究。

缩写

密件抄送：

体心立方

cif:

晶体学信息文件

fcc：

面心立方

FE：

分数曝光，分散

hcp:

六方密堆积

ORR：

氧化还原反应

rW(G):

反向维纳指数

Sz(G)：

塞格德指数

W(G)：

维纳指数

WW(G)：

超维纳指数