纳米盒的神奇数学公式
摘要
中空纳米结构处于许多科学努力的前沿。它们由纳米盒、纳米笼、纳米框架和纳米管组成。我们研究了纳米盒中原子配位的数学原理。这种结构由一个带有 n 的空心盒子组成 贝壳和 t 外层。我们推导出的神奇公式取决于 n 和 t .我们发现带有 t 的 nanoboxes =2 或 3,或只有几层的墙通常具有大量配位原子。纳米结构中低配位的好处仅在壁厚比正常合成的壁厚薄得多的情况下才会出现。 t 的情况 =1 是独一无二的,并且具有独特的魔法公式。这种低配位的纳米盒具有多种应用,包括电池、燃料电池、等离子体、催化和生物医学用途。鉴于这些公式,可以确定纳米盒的表面分散。我们希望这些公式有助于理解原子配位如何随 n 变化 和 t 在一个纳米盒内。
介绍
纳米盒最初是在 2002 年左右合成的 [1, 2]。纳米盒与纳米笼的不同之处在于后者具有多孔壁。此外,两者都与纳米框架不同,因为纳米框架是由簇的低坐标轮廓组成的结构(框架)。这种各向异性的多面体结构可能是由电流置换反应产生的 [3, 4]
$$\begin{array}{l}\\ {\hbox{Anode}}:yA_{(s)}\rightarrow yA_{({{\rm aq}})}^{x+}+xye_{({{ \rm aq}})}^{-} \\ {\hbox{阴极}}:xB_{({{\rm aq}})}^{y+} + xye_{({{\rm aq}})} ^{-} \rightarrow xB_{(s)} \\ {\hbox{Full\,Reaction}}:yA_{(s)}+xB_{({{\rm aq}})}^{y+} \rightarrow yA_{({{\rm aq}})}^{x+}+xB_{(s)} \\ \end{array}$$ (1)
其中含有金属 A 的纳米团簇 被金属B的水溶液牺牲性掏空 , 具有更高的还原电位并产生元素 B 的空心实体 .半反应发生在电化学电池的阳极和阴极,导致如上 [5] 的完全组合反应。在某些情况下,科学家们通过金属和空位的 Kirkendall Fickian 扩散将电流位移与空洞形成相结合 [6]。这种活动的模型存在于特定案例中,并且已经报道了原位电子显微镜实验 [7, 8]。其他合成方法包括化学蚀刻 [9]、离子交换 [10] 和金属有机骨架 (MOF) [11, 12]。最近对合成方法的评论提到,尚未在尺寸区域 \(2
这种中空结构具有低配位性,使它们在电池 [12]、燃料电池 [14]、等离子体 [15]、催化 [16] 和生物医学应用 [17] 中受到关注。先前的分析表明,对于催化应用,采用协调方法 [18],而对于能量存储,密度泛函理论 (DFT) 结果只有一些提示,表明选择方面很重要 [19]。我们使用先前从邻接矩阵分析中推导出的方法 [20, 21] 来发现具有 n 的盒子的原子配位 壳和壁厚 t 层。该分析表明,带有 t 的 nanobox =2 或 3 具有整体配位,因此低配位的好处仅适用于壁比通常认为必要的更薄的纳米盒。我们使用的方法通过幻数和公式对十三种纳米盒的原子配位进行量化。
方法
我们通过协调方法进行分析的关键是从纳米盒的原子坐标创建邻接矩阵。如下创建这样的矩阵。我们定义 i 和 j 作为最近的邻居,并通过要求键长 \(r_{ij}
由于我们创建了最近邻邻接矩阵,我们知道顶点 i 的坐标数 \(\hbox {cn}_i\) 通过对 \({{\mathbf{A}}}(i,:)\) 的元素求和。我们的结构由编号为 0, 1, ..., n 的 \(n+1\) 个壳组成 , 与 t 外层。令 \(N_{{\rm cn}_i}(n,t)\) 是配位原子数 \(\hbox {cn}_i\) 其中 \(1\le \hbox{cn}_i\le \hbox{cn}_M\) 与 \(\hbox {cn}_M\) 纳米盒中的最大协调。那么纳米盒中的原子总数由下式给出
$$N_T(n,t) =\sum _{{\rm cn}_i=1}^{{\rm cn}_M}{N_{{\rm cn}_i}(n,t)}.$$ (4)纳米盒外壳(或内部)的表面原子,n 具有一组小于体配位的键。因此表面原子的最大配位为\(\hbox {cn}_s <\hbox{cn}_M\),表面原子数为
$$N_S(n,t) =\sum _{{\rm cn}_i=1}^{{\rm cn}_s}{N_{{\rm cn}_i}(n,t)}.$$ (5)如果所有非表面顶点的坐标都大于 \(\hbox {cn}_s\),这适用于所有 fcc、bcc 和 hcp 集群。我们通过计算和为 \(\hbox {cn}_i\) 的邻接矩阵的列来确定 \(N_{{\rm cn}_i}(n,t)\)。请注意,我们的聚类坐标算法是由壳层构建的,因此每个后续壳层都包含 n 的所有先前较低值 .此外,框中的债券数量是
$$N_{{\rm B}}(n,t) =\frac{1}{2}\sum _{{\rm cn}_i=1}^{{\rm cn}_M}{\hbox{ cn}_i\cdot N_{{\rm cn}_i}(n,t)},$$ (6)其中 \(N_{{\rm B}}(n,t)\) 是键数,\(\hbox {cn}_M\) 是最大配位。 1/2 的因子是由于成对最近邻键而产生的。
因为我们知道这些方程依赖于 n , t 作为一个最多为 3 次的多项式,我们可以为 n 的 4 个连续值计算 \(N_{{\rm cn}_i}(n,t)\) , 说 \(n=n_0+j\), j =0, 1, 2, 3。一个简单的插值多项式将给出多项式系数。必须验证通过增加 \(n_0\)(通常等于 1),公式不会改变。如果公式从 \(n_0\) 开始变得稳定,那么它们对所有 \(n\ge n_0\) 都成立。为了得到精确的有理系数,需要对系数进行精确算术求解Vandermonde系统。
Note that in the magical formulas for nanoboxes we have that \(n> t\) so that therefore contrary to any expectation, filling up the box by an appropriate choice of t 不会为完整的实体簇重新创建原始的魔法公式。这些神奇的公式可用于对簇和盒子或笼子的中尺度特性进行建模。完整的公式集最初是为 19 种簇类型导出的。在这份手稿中,我们推导出了十三种纳米盒的神奇公式。
在下面的神奇公式中,我们发现对于 t =2 或 t =3 层壳厚度。大多数用于 t 的层 =2;例外是 fcc 立方体、立方八面体、二十面体以及 bcc 立方体和截断立方体。在后者中,批量协调只出现在 t =3 层。对于下面的数据,神奇公式的表格都附有一个“半盒子”的图形,以显示纳米盒子的内部。旁边是一个颜色条,指示括号中此类的坐标和数量。
结果与讨论
为了描述神奇公式的适用性,我们概述了催化行为如何依赖于协调和此类公式。我们定义 G 作为簇的大小相关的吉布斯能量。由于吸附原子与外壳原子结合,G 增加 称为吸附能,记为\(\Delta G\)。这可以分为外壳上与吸附原子键合的原子的不同配位类型。例如,扭结原子以\(\Delta G_{k}\) 的量增加吸附能。类似地,边缘原子添加 \(\Delta G_{e}\),而小平面原子贡献 \(\Delta G_f\) 然后 [18]:
$$\Delta G=\sum _{o\in \{f,e,k\}} \Delta G_o N_o$$ (7)其中 \(N_o\) 是指定类型外壳中的原子数。外壳中与吸附原子键合的原子总数定义为\(N_s=N_f+N_e+N_k\),结果:
$$\begin{aligned}\Delta G=&{} \Delta G_f\cdot (1-f_e-f_k)+\Delta G_e\cdot f_e+\Delta G_k\cdot f_k \\&\quad {\hbox{where} } \,\,f_o=N_o/N_s, \,\,o\in \{e,k\},\end{aligned}$$ (8)吉布斯能量分数通过边缘和扭结位点表示,这些位点对特定结构具有明确的协调。这表明魔术公式通过边缘和扭结配位及其公式在表面反应中起作用。请注意,方程。 (8) 适用于吸附到顶部位点,否则并非所有吸附原子都会与外壳中的原子结合。在这样的模型中,扭结点具有与壳数 n 一致的神奇公式 , 边缘站点的公式与 n 成线性 , 和 facet 位点具有与 n 二次方的公式 .更具体地说,扭结位点是最低配位公式,边缘位点是第二低配位,面位点对于(100)个面有cn =8,对于(111)面有cn =9。
可以应用基于每个粒子的两个基本关系。对于吉布斯能量和吸附常数,\(K_{{\rm a}}\),它成立:
$$K_{{\rm a}}={\exp } \left( -\frac{\Delta G}{RT}\right) ,$$ (9)其中 R 是气体常数和 T 是以开尔文为单位的温度。此外,Brønsted-Evans-Polanyi 关系广泛用于均相和多相催化 [18, 22] 使用反应常数 k 的关系 和平衡常数 K 如下:
$$k=gK^{\alpha },\quad 0<\alpha <1,$$ (10)其中 g 和 \(\alpha\) (Polanyi 参数)是常数。 Polanyi 参数是无单位的,是一个真分数,最初由 Brønsted [23] 给出。然后我们有:
$$k=k'_{a}{\exp } \Bigl (-\alpha \bigl ({f_n^{e}\cdot \chi _{_e}({D_n}) +f_n^{k}\cdot \chi _{_k}({D_n})}\bigr )\Bigr ),$$ (11)哪里
$$\begin{aligned} &\chi _{_e}(D)=\frac{\Delta G_e(D)-\Delta G_f(D)}{RT},\\&\chi _{_k}(D )=\frac{\Delta G_k(D)-\Delta G_f(D)}{RT}, \end{aligned}$$ (12)和
$$k'_{a}=g\exp \left( -\alpha \frac{\Delta G_f}{RT}\right) .$$ (13)该分析表明,确定催化模型需要一种计算吉布斯能量的方法。已经考虑了已知的催化反应,如两步和Langmuir-Hinshelwood 机制[24]。
FCC Nanoboxes
面心立方结构是纳米团簇和纳米盒最常见的形式。这是具有有趣特性的金属的结构,例如具有等离子体特性的贵金属和具有催化作用的贵金属。由于与标准氢电极 (SHE) [5] 相比,金具有 1.50 V(见方程式 1)的高还原电位,因此它是最容易合成为纳米盒或纳米笼的金属之一。金纳米盒或纳米笼已经形成立方体[1]、正八面体[25]、二十面体和十面体[26]、八面体[27]和四面体[28]形状。
我们可以通过使用最近邻键长 r 的协调方法来确定这些纳米盒的大致尺寸 (cn) [29],
$$r(cn) =\frac{2r_{{\rm B}}}{\left( 1+\exp \left( \frac{12 - \langle cn \rangle _c)}{8\cdot \langle cn \rangle _c}\right) \right) }.$$ (14)这里\(r_{{\rm B}}\) 是金的体键长(0.2884 nm),\(\langle cn \rangle _c\) 是簇的平均坐标。我们发现 D 之间存在线性关系 和 n ,簇壳数,如表1所示:
$$D(n)=a \cdot r_{{\rm B}} \cdot n + b.$$ (15)我们使用带有 t 的 nanoboxes =3,因为公式随 t 而变化 ,我们希望实现一些批量协调。用于计算 D (n ),我们使用簇中原子之间的最大距离,该距离来自欧几里德矩阵。注意 D (n ) 是一个经验公式,来自数据 (variable n 并计算 D ),因此未经证实。
这些关系产生的直径与来自 DFT 的其他数据一致。对于带有 N 的实心立方八面体 等于 55、561 和 923,我们得到 1.12 纳米、2.85 纳米和 3.43 纳米的直径。这与公布的 55 个原子的 1.1 nm [30]、561 个原子的 2.7 nm [31] 和 923 个原子的 3.5 nm [30] 的 DFT 结果相比更有利。下面列出了一些 fcc 纳米盒的神奇公式(表 2、3、4、5、6、7、8)。
二十面体和十面体纳米盒
参见表 9 和 10。
钻石和简单立方纳米盒
金刚石立方晶格结构由碳的同素异形体以及元素硅和锗形成。此外,一些立方化合物形成这种结构,如立方氧化铁、四面体金刚石磁赤铁矿 \(\gamma\)-Fe2O3。四面体金刚石磁赤铁矿中 Fe-O 的键长 \(\gamma\)-Fe2O3 =0.186 nm [32]。这导致金刚石簇的直径 D (n ) 如下:
$$D(n) =3.3984\cdot n_{{\rm B}} \cdot n - 0.21194.$$ (16)根据参考文献[12],立方氧化铁的微盒子形成并具有有趣的锂存储能力。我们不知道能量存储的完整协调模型,但如上所述,DFT 结果表明活动可能取决于小平面方向 [19]。目前不存在像我们对催化那样依赖于协调的存储模型。从上面的等式 (16)(使用 t 创建 =4),一个 microbox 大约需要 n =1600 贝壳,用于钻石磁赤铁矿。下面列出了金刚石和简单立方晶格结构的神奇公式(表 11、12)。
密件抄送纳米盒
参见表 13、14 和 15。
HCP Nanoboxes
见表 16。
案例t =1
特殊情况 t =1 是独一无二的,因此具有独特的神奇公式。我们针对上述一些纳米盒检查了这种情况。具有超薄壁的纳米盒已形成为立方体 [33]、八面体 [16] 和二十面体 [34]。根据下面的神奇公式,带有 t 的立方纳米盒 =1 的协调性最低。与 SHE 相比,铂具有 1.18 V 的相对较高的还原电位,因此它可以通过电置换形成,参见方程式。 (1) [5]。然而,其中一些铂基纳米笼的氧化还原反应 (ORR) 特性表明,具有 (111) 晶面的结构比具有 (100) 晶面的结构具有更好的 ORR 质量活性 [35]。
因此,具有 20 (111) 个面的二十面体具有最佳的 ORR 质量活动,其次是八面体,最后是截头立方体。下面的表格数据证明了这种来自小平面取向的催化行为优先于配位数的特性。换句话说,如下表所述,具有(100)个面的立方体的魔配位数最低,为4和5,而具有(111)个面和更大魔方的八面体和二十面体具有更好的ORR活性。这种特性也在纳米团簇中得到证实,其中 DFT 结果证实了 (111) 面的优势 [36],尤其是对于 PtNi 合金(表 17、18、19、20、21)。
分散
鉴于边缘和扭结位点相对于小平面位点在催化活性方面的重要性,我们已经确定了我们研究的一些纳米盒的表面分散。 (100) 个面的 cn =8,而 (111) 个面的 cn =9。当在纳米盒之间进行比较时,这可能有助于深入了解单个多面体活性的原因。在下面的图 1 中,我们绘制了表面色散 \(D_{{\rm s}} =(N_{{\rm e}} + N_{{\rm k}}) / N_{{\rm S}} \cdot 100\%\)。在这种关系中,\(N_{{\rm k}}\) 是扭结或角点的数量,\(N_{{\rm e}}\) 是边缘站点的数量。从图 1 中可以看出,具有 (111) 面的纳米盒比具有 (100) 面的纳米盒具有更高的分散性,这证明了 (111) 面的催化活性偏好。
<图片>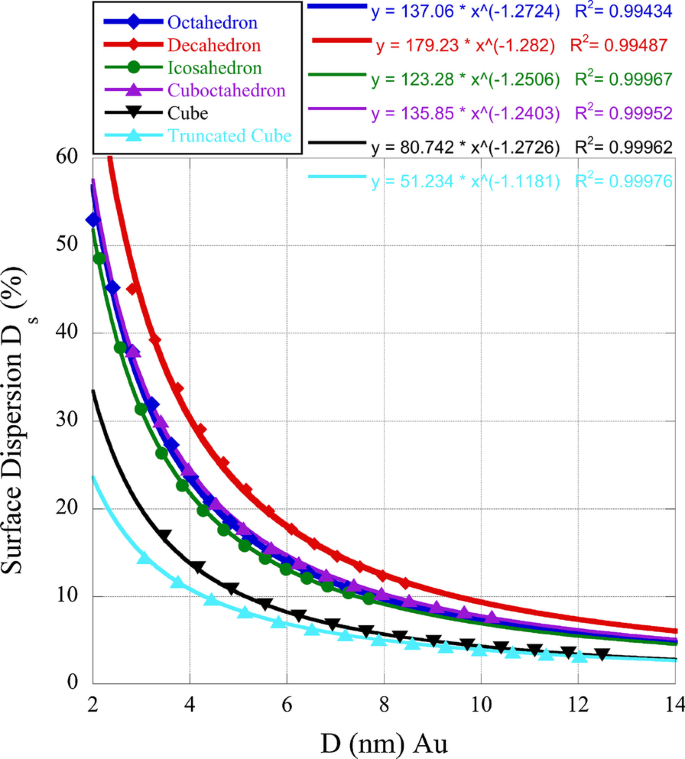
金纳米盒的表面分散
结论
总而言之,我们首次对纳米盒的神奇公式进行了详细的数学描述。壳厚的情况,t =1 与 \(t>1\) 不同,我们将其中一些情况的数据制成表格。配位、原子数和键数的公式都列举出来了。我们发现对于 t 的层出现批量协调 =2 或 3,因此比通常合成的要薄得多。只有非常薄的壁才能实现低协调的好处。我们希望这些结果对建模和实验工作有用。
数据和材料的可用性
支持本文结论的数据集可从通讯作者处获取。
缩写
- 密件抄送:
-
体心立方
- fcc:
-
面心立方
- hcp:
-
六角密堆积
- DFT:
-
密度泛函理论
- 她:
-
二次氢电极
纳米材料


