横向电子聚焦中自旋分裂峰的温度依赖性

背景

通过使用在 GaAs/AlGaAs 异质结构界面处形成的二维电子气 (2DEG) 实现的准一维 (1D) 系统的电子传输已得到广泛研究。一维系统提供了一个出色的平台，不仅可以设想非相互作用的量子力学系统，其中电导量化 [1-3] 的单位为 \(n\times \frac {2e^{2}}{h}\ )，其中 n =1,2,3... 是不同的一维能量子沙，也是探索多体物理的场所 [4-9]。最近，由于预测和实验证明低密度一维系统中的富相导致早期 Wigner 结晶，多体一维系统的物理学进展获得了动力 [6, 7, 10]。此外，多体一维系统框架中 0.7 电导异常的起源仍存在争议[11-15]。 0.7 异常有两个主要特征：第一，在面内磁场的存在下，0.7 异常演化为\(0.5\times \frac {2e^{2}}{h}\) 平台，表明它与自旋有关 [4]；其次，发现 0.7 异常随着温度的降低（升高）而减弱（加强）[4]。这些非凡的观察导致了大量的理论和实验尝试来探索与 0.7 异常相关的内在自旋极化；然而，对于这种异常的起源并没有达成共识[11-15]。因此，为了进一步了解 0.7 异常，必须对一维通道内的自旋极化进行直接测量。

提出了一种基于横向电子聚焦 (TEF) 的方案来解决自旋极化 [16, 17]，并在 p 型 GaAs [18, 19] 和 n 型 InSb [20] 中得到验证。在该方案中，可以从第一聚焦峰的两个子峰的不对称性中提取由交换相互作用引起的自旋极化。最近，我们表明可以以第一个聚焦峰中分裂的形式检测到自旋已在空间上分离的一维电子的注入，其中两个子峰代表检测到的自旋态的总体[21]。在目前的工作中，我们报告了自旋分裂第一聚焦峰的温度依赖性，并基于两种自旋物种之间存在的自旋间隙分析了结果。

方法

本工作中研究的器件是由在 GaAs/Al 0.33 Ga 界面处形成的高迁移率二维电子气 (2DEG) 制成的 0.67As 异质结构。在 1.5 K 时，测得的电子密度（迁移率）为 1.80×10 ¹¹ 厘米 ⁻² (2.17×10 ⁶ 厘米 ² V ⁻¹ s ⁻¹ ) 因此，平均自由程超过 10 μ m 远大于电子传播长度。使用标准锁定技术在晶格温度为 20 mK 的无冷冻稀释冰箱中进行实验。温度依赖性测量范围为20 mK至1.8 K。

结果与讨论

图 1a 显示了实验设置以及使用插图中显示的设备获得的典型聚焦光谱。聚焦装置是专门设计的，因此可以单独控制注射器和检测器，以避免它们之间可能发生的串扰 [21-23]。用于注入器和检测器的量子线具有 500 nm 的宽度（限制方向）和 800 nm 的长度（电流流动方向）。进样器和检测器都显示出明确定义的电导平台，如图 1b 所示。图 1 的标题中给出了有关该设备的更多详细信息。

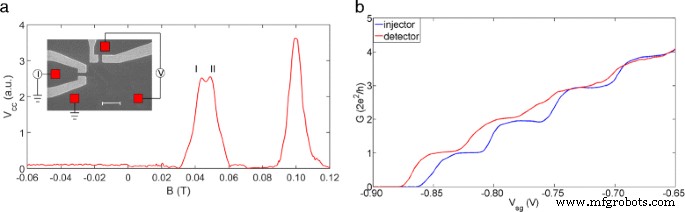
实验设置和设备特性。 一 将注射器和探测器都设置为 G 0 (2e ² /H）。 V 抄送 是检测器两端的电压降。聚焦峰在正磁场下可以很好地定义，而在负磁场下信号可以忽略不计。第一个峰显示出明显的分裂。两个子峰已突出显示为峰 I 和峰 II。插图显示了器件的 SEM 图像。进样器和检测器之间的间隔为1.5 μ 米。红色方块形成欧姆接触，而左侧和顶部的两对灰色门分别形成注射器和检测器。比例尺为 2 μ 米。 b 进样器和检测器的电导特性

在负磁场下，测量信号几乎为零，因为电子向相反方向弯曲，从而错过了检测器。同样明显的是，舒布尼科夫-德哈斯振荡和量子霍尔效应对观察没有贡献。在存在小的正横向磁场 (B⊥) 的情况下，电子从注射器聚焦到检测器，导致在 B⊥ 中出现周期性聚焦峰，而在负磁场端检测到的信号可以忽略不计。使用关系[23]，

与实验结果吻合良好。在这里，e 是基本电荷，\(\hbar \) 是约化的普朗克常数，L 是进样器和检测器之间的间隔（在 90° 聚焦装置几何结构中，这是沿对角线方向的间隔）。除了作为半经典电子回旋轨道表现形式的周期性聚焦峰外，有趣的是注意到奇数聚焦峰的分裂。有人认为这种奇数聚焦峰的异常分裂源于自旋轨道相互作用 (SOI) [16, 17] 并且已在 GaAs 空穴气 [18, 19] 和 InSb 电子气 [20] 中成功观察到。我们最近展示了 n-GaAs 中奇数聚焦峰的分裂 [21]，其中使用具有部分极化和空间分离的一维电子的较长量子线将极化的一维电子注入二维区域，然后在探测器中进行测量。第一个聚焦峰的分裂形式。在这里，我们有兴趣通过横向电子聚焦研究一维通道内自旋态的热效应。我们注意到，当热能 k B T 超过 2 Δ E (Δ E是两个自旋分支之间的能量差）与理论预测一致[17]。

在我们讨论温度依赖性效应之前，了解导致观察到的峰分裂的机制很重要。图 2a、b 显示了形成进样器（底部对）和检测器（左对）的分裂门的电位分布。在 SOI 存在的情况下，两种自旋物质遵循不同的回旋半径，如图 2a 所示，从而在第一个聚焦峰中产生两个子峰。然而，第二个聚焦峰的情况不同，其中涉及由分裂栅极产生的静电势边界处的散射，如图 2b 所示。在这种情况下，自旋向上电子（颜色图中的红色箭头）最初遵循较小的回旋半径，而在散射后它具有更大的半径 [16, 17]，反之亦然，自旋向下电子（白色箭头） ，因此两个自旋物质在检测器处重新结合。峰分裂的底层推理可以在图 2c、d 的 k 空间中找到。在这里，我们假设自旋轨道相互作用是 Rashba 型的；然而，该分析也适用于批量德雷塞尔豪斯效应。对于第一个聚焦峰（图 2c），两个自旋物种从 (0, k y ) 到 (-k x , 0) 沿不同的费米面。对于第二个聚焦峰（图 2d），同样的论点在散射之前成立；然而，在散射后，动量改变其符号而自旋方向保持不变[16]。因此，最初占据费米内表面的自旋电子（红色箭头）在散射后跳跃到外费米表面，以确保动量的符号和自旋方向都处于正确的顺序（跳跃由图 2 d) 中的蓝色粗箭头，自旋向下电子反之亦然。回旋半径与动量成正比，因此回旋半径在坐标空间中发生变化，这是由于两个费米面之间的跳跃导致单个第二聚焦峰的结果。

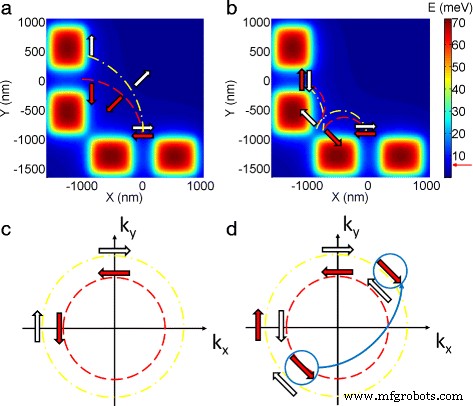
峰分裂的机制。 一 , b 分别为第一和第二聚焦峰在坐标空间中的峰分裂。红色和白色箭头代表自旋向上和自旋向下的电子，彩色块代表静电势，红色虚线表示回旋半径较小，黄色虚线表示回旋半径较大。 c , d 分别为第一个和第二个聚焦峰在 k 空间中的峰分裂。电子从 (0, k y ) 到 (-k x , 0) 图中逆时针 (c ）。在情节 (d )，粗蓝色箭头突出了在注射器和探测器之间形成的静电势边界处反射后的转变

图 3 a-c 分别显示了注入器设置为 0.5G 0、G 0 和 1.8G 0 时聚焦结果的温度依赖性，其中晶格温度从 20 mK 增加（电子温度校准为大约 70 mK）到 1.8 K，图 3 d-f 分别显示了图 3 a-c 中数据的放大。对于 G i =0.5G0（图3a）观察到单个峰（因为只有一个自旋子带被占据），其在较高温度下逐渐变宽。此外，聚焦峰向光谱中心移动，并在较高温度下变得更加对称（见底部轨迹，T =1.8 K，图 3 a、d)。这可能是由于在相对较高的温度下两个自旋子带之间可能发生电子跃迁。相比之下，对于G 我 =G 在图 0（图 3b）中，每个代表自旋状态的子峰都存在于 20 mK 到 1.2 K 之间。然而，导致两个子峰的第一个聚焦峰的下降在 1.8 K 处被抹去（图3b、e）。随着 G 我 设置为 1.8 G 0（图3 c），分裂没有很好地解决，左子峰（I）在光谱中占主导地位。我们注意到，随着温度的升高，峰值 I 的幅度逐渐减小，导致在 1.8 K 处出现一个不对称的第一聚焦峰。在 n 型 InSb 中，即使在 10 K 处分裂也很明显，这与峰值的事实一致分裂约为 60 mT，表明 InSb [20] 中存在强 SOI，比本案例中测量的 5.5 mT 的峰值分裂大一个数量级。

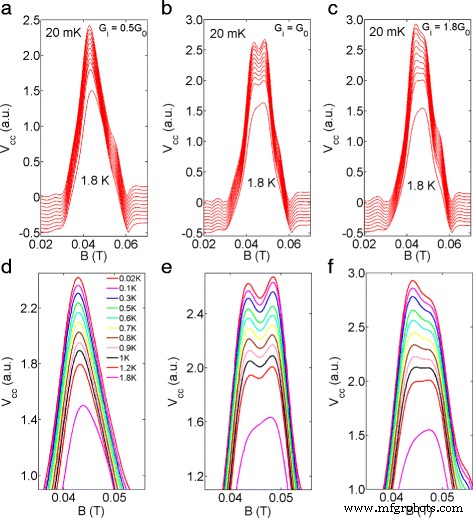
TEF 的温度依赖性。 一 –c 喷油器设置为 0.5 G 0、G 0 和 1.8G 0 分别。晶格温度从 20 mK（顶部轨迹）增加到 1.8 K（底部轨迹）。为清楚起见，数据已垂直偏移。 d -f , 放大 (a )-(c )

考虑到两个子峰可能部分重叠，为了准确提取峰宽和幅度，我们使用两个洛伦兹峰来重建实验数据，如图 4a 所示，使用关系，

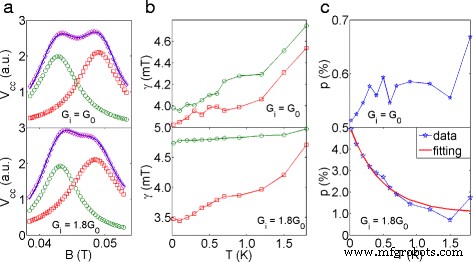
温度依赖性数据的分析。顶部的图是 G 我 =G 0，最下面的是G 我 =1.8 G 0. a 用 20 mK 的两个洛伦兹峰重建第一个聚焦峰。蓝色实线是实验数据，绿色圆形标记是峰 I 的拟合，红色方形标记是峰 II 的拟合，品红色菱形标记突出了重建的聚焦峰。 b FHWM，γ 作为温度的函数：在两种情况下，子峰都随着温度的升高而变宽。标记代表与图中相同的含义 (a ）。 c 用 G 测量的极化 我 =G 0 在 0.6 % 附近波动 .另一方面，使用 G 测量的极化 我 =1.8 G 0 遵循指数衰减

其中 A i 是峰值 i 的幅度 (i =1, 2 分别为峰 I 和峰 II), γ 我 表示半峰全宽 (FWHM)，B 我 是峰的中心。从拟合中可以提取出两个值得注意的结果：首先，从图 4b 中可以看出 γ （有关表示峰 I 和峰 II 的迹线和符号的详细信息，请参见图 4 的标题）峰 I 和峰 II 均随温度升高而增加，而与进样器电导无关，这表明子峰的热展宽阻止了观察高温下出现峰分裂。可以注意到 G 的峰值 I 我 =1.8G 与其他峰（G 的两个峰）相比，0 对温度相对稳健 0 和峰值 II 为 1.8G 0）。二、测得的自旋极化p \(\left (p=\left |\frac {A_{1}-A_{2}}{A1+A_{2}}\right | \right)\) 与 G 我 =G 0 在 0.6 % 附近波动 并且没有显示出明确的温度依赖性，这与电导平台的自旋极化应保持在 0 的事实一致，而不管温度如何（图 4c，上图）。另一方面，当 G 我 设置为 1.8 G 0，提取的自旋极化从 5 衰减到 0.8 % （图4d，下图）遵循关系[15]，

其中 α 是振幅的前置因子，k B 是玻尔兹曼常数，Δ E 是两个自旋分支和 c 之间的能量差 考虑了由于实验中的不确定性而产生的小残值。我们提取了Δ的值 E 约为 0.041 meV（对应于 0.5 K）。理论 [17] 预测分裂应该持续到 k B T 超过 2 Δ E （即在我们的例子中为 1 K）这与我们的结果非常吻合，即在 1.2 K 时可以观察到峰分裂。

结论

总之，我们展示了横向电子聚焦的温度依赖性，其中两个自旋态的贡献表现为第一个聚焦峰中的两个子峰。观察到峰分裂在 20 mK 到 1.2 K 范围内被很好地定义，超过这个温度，峰分裂被抹去。此外，在较高温度下，聚焦峰有变得更加对称的趋势，表明由于热激发，两个自旋分支之间可能达到平衡。

这项工作由英国工程和物理科学研究委员会 (EPSRC) 资助。