表面能降低驱动的凹坑图案 Si(001) 衬底的形态演化
摘要
异质外延岛的横向排序可以通过在沉积之前对衬底进行适当的凹坑图案化来方便地实现。控制凹坑的形状、方向和大小并非微不足道,因为它们是亚稳态的,可以在沉积/退火过程中显着演变。在本文中,我们利用连续模型来探索在 Si(001) 上可以预期的典型亚稳态凹坑形态,具体取决于初始深度/形状。演化是使用表面扩散模型预测的,在相场框架中制定,并解决表面能各向异性问题。结果显示很好地再现了文献中报道的典型亚稳态形状。此外,发现不同深度的坑剖面的长时间尺度演化遵循相似的动力学路径。该模型还用于处理异质外延生长的情况,其中涉及两种材料,其特征在于平衡 Wulff 形状的不同面。这会导致形态的显着变化,例如沉积过程中凹坑的旋转,如 Ge/Si 实验所证明的那样。
背景
几种半导体(例如 Ge/Si 或 InGaAs/GaAs)的晶格失配异质外延可导致 3D 岛的形成,遵循 Stranski-Krastanow (SK) 生长模式。虽然通过纯自组装获得这种点的可能性 [1, 2] 特别有吸引力并引起了广泛的兴趣,但人们很快意识到随机成核会严重阻碍应用,以及尺寸和形状的分散。
数十年的研究导致开发了多种方法来驱动异质外延生长以形成有序结构 [3-7]。其中,凹坑图案衬底的使用已被证明是实现异质外延岛的高有序化和尺寸控制的最通用方法之一[8-15]。
凹坑图案基板通常通过诸如纳米压印光刻 [16-18]、电子束光刻 [13, 14] 结合反应离子蚀刻 (RIE) [19, 20] 或湿化学蚀刻 [21, 22] 和纳米压痕 [23, 24],即通过自上而下的方法。使用这些方法,可以高精度地设计凹坑的有序图案,并在适当的生长条件下 [14, 25] 导致几乎完美的横向排序。
由于凹坑的实际形状确实会影响系统的能量,更一般地说,会影响岛形核的形成 [26, 27],因此控制它们的形态至关重要。这并非微不足道:毕竟,凹坑只是在基板上钻出的孔。因此,在足够高的温度下,毛细血管 [28] 预计会产生形态演变,最终导致完全愈合。实际上,为了获得可重复的、长寿命的亚稳态形状,通常使用退火工艺或在初始凹坑形成后进一步沉积基板材料 [8, 26]。请注意,即使凹坑形状稳定,在实际的异质外延过程中也可以进一步演化 [29, 30]。
在这项工作中,我们旨在描述通过表面扩散的表面能减少驱动的凹坑图案基板的演变。我们采用合适的相场方法 [31],允许模拟与实验 [32] 兼容的长度和时间尺度。该模型已被用于解释异质外延系统形态演化过程中的扩散限制动力学 [33-36]。此外,它已被证明可以正确描述包括现实各向异性表面能在内的平衡演化[37-39]。
在不失一般性的情况下,我们将重点关注在文献[8, 10, 14, 30, 40, 41]中广泛研究的凹坑图案Si(001)表面的相关案例。
工作安排如下。在“相场模型”部分,我们简要说明了用于描述包括各向异性表面能在内的表面扩散演化的相场模型。此外,我们描述了在所考虑的方法中如何考虑实际的 Si Wulff 形状。在“Si(001) 凹坑的平滑化”部分,通过考虑不同的初始配置讨论了由表面能降低驱动的 Si(001) 凹坑的预期平滑度,概述了达到平衡的动力学路径。在“模拟由于 Ge 过度生长引起的形状变化”部分中,考虑了该方法在异质外延生长的特定情况下的应用,该情况对应于在 Si 凹坑上沉积薄层 Ge 时的表面能驱动的形状变化。结论和评论总结在“结论”部分。
方法
相场模型
相场模型考虑连续阶参数φ , 在 φ 之间变化 =1(实心)和 φ =0(真空)[31, 32]。该方法基于能量泛函 [37],
$$ \begin{aligned} F=&\int_{\Omega} \gamma(\hat{\mathbf{n}}) \left(\frac{\epsilon}{2} |\nabla \varphi|^{2 } + \frac{1}{\epsilon}B(\varphi) \right) d\mathbf{r} + \\ &+\int_{\Omega} \frac{\beta}{2\epsilon} \left( -\epsilon\nabla^{2}\varphi+\frac{1}{\epsilon}B'(\varphi)\right)^{2} d\mathbf{r}, \end{aligned} $$ (1)与 \(\Omega \in \mathbb {R}^{3}\) φ 的定义域 (r ) 和 r =(x ,y ,z )。第一项对应于由 φ 定义的扩散界面域内的相之间的界面能 ,即固相的表面能。 \(\gamma (\hat {\mathbf {n}})\) 是表面能量密度,\(\hat {\mathbf {n}}\) 是向外指向的表面法线,ε 相间界面的厚度。 B (φ )=18φ 2 (1-φ ) 2 是在 φ 中具有最小值的双阱势 =0 和 φ =1 如参考文献。 [31]。等式中的第二项。 (1) 是在强各向异性机制中需要的 Willmore 正则化,以避免形成尖角 [37, 38, 42]。 β 是圆角对应的参数。
φ 的演变 再现表面的扩散受限动力学,由退化的 Cahn-Hilliard 模型给出,即,
$$ \frac{\partial \varphi}{\partial t}=D \nabla \left[ M(\varphi) \nabla \mu \right], $$ (2)其中 μ =δ F /δ φ 是化学势,D 是扩散系数,M (φ )=(36/ε )φ 2 (1-φ ) 2 是限制在表面的迁移率函数。 μ 的方程 阅读
$$ \begin{aligned} g(\varphi)\mu =\delta F/ \delta \varphi=&-\epsilon \nabla \cdot \left[\gamma(\hat{\mathbf{n}}) \nabla \varphi \right] + \frac{1}{\epsilon} \gamma(\hat{\mathbf{n}}) B'(\varphi) + \\&-\epsilon \nabla \cdot \left[|\ nabla \varphi|^{2} \nabla_{\nabla \varphi} \gamma(\hat{\mathbf{n}}) \right] + \\ &+\beta\left(-\nabla^{2} \ kappa + \frac{1}{\epsilon^{2}} B^{\prime\prime}(\varphi) \kappa \right), \end{aligned} $$ (3)与 κ =-ε ∇ 2 φ +(1/ε )B ′ (φ ) 和 g (φ )=30φ 2 (1-φ ) 2 [33, 37, 38]。后者是一种稳定功能,可确保界面厚度的二阶收敛,而不影响对通过表面扩散的材料传输的描述 [43, 44]。平衡状态下垂直于界面方向的剖面由
很好地描述 $$ \varphi(\mathbf{r})=\frac{1}{2}\left[1-\tanh \left(\frac{3 d(\mathbf{r})}{\epsilon} \right) \right], $$ (4)其中 d (r ) 是到相间界面中心的有符号距离。该方程用于设置φ的初始条件 如下所述。我们将固相的表面称为 φ ~0.5 等值面。所考虑表面的所有几何特性都可以从 φ 导出 ,例如外向曲面法线 \(\hat {\mathbf {n}}=- \nabla \varphi / | \nabla \varphi |\).
各向异性表面能
为了描述各向异性表面能,我们考虑了表面能密度的定义,\(\gamma (\hat {\mathbf {n}})\),如 [38, 39] 中介绍的:
$$ \gamma(\hat{\mathbf{n}})=\gamma_{0} \left(1-\sum_{i}^{N} \alpha_{i} \left(\hat{\mathbf{n }} \cdot \hat{\mathbf{m}}_{i} \right)^{w_{i}} \Theta\left(\hat{\mathbf{n}} \cdot \hat{\mathbf{m }}_{i}\right) \right)。 $$ (5)其中优先取向 \(\hat {\mathbf {m}}_{i}\),即表面能密度最小的方向,可以随它们的相对深度一起任意设置, α 我 , 相对于 γ 0. 参数w 我 控制 \(\gamma (\hat {\mathbf {n}})<\gamma _{0}\) 围绕 m 的区域的扩展 我 方向,即它们是最小值的宽度(另见参考文献 [38])。
为了说明 Si 晶体的特定各向异性,我们设置了最小能量方向 m 我 ,对应于〈001〉、〈113〉、〈110〉和〈111〉[45]。 α 我 系数,确定最小值的深度,由 [39]
获得 $$ \alpha_{i}=1-\left(\frac{\gamma_{i}}{\gamma_{\langle 001\rangle}}\right)\left(1-\alpha_{\langle 001 \rangle} \right), $$ (6)其中 α 〈001〉=0.15 设为参考,各种γ 我 对应于参考文献中报道的上述取向的表面能值。 [45]。不失一般性,我们设 γ 0=1。事实上,最小值和各向异性强度的比率可以由 α 控制 我 来自方程的值。 (6) 和 α 〈001〉,而 γ 0 在等式中扮演前置因子的角色。 (2),因此只影响演化的绝对时间尺度。
等式中能量最小值的宽度。 (5) 设置为 w 我 =50 对于所有最小方向,除了 w 〈113〉=100 [39]。根据参数的这个定义,在 Wulff 形状中预测尖角,即表面能各向异性是“强”的 [38, 42, 46]。因此,Willmore 正则化对于执行模拟是绝对必要的。 β 值设置角部圆角区域的扩展,已知其半径与 \(\sqrt {\beta }\) [37] 成正比。为了进行模拟,由β在拐角处舍入设置的长度比例 必须大于数值方法的空间离散化的分辨率。然而,值得一提的是,Wulff 形状中可能存在的小面以 \(\sqrt {\beta }\) 的顺序扩展可能会在使用太大的 β 时导致隐藏 值以及涉及 Wulff 形状中实际存在的优先取向的小尺度刻面。在这项工作中,我们设置 β =0.005。根据模拟域的大小,下面指定,这个值允许我们采用可行的空间离散化。此外,所有优先方向进入方程。 (5) 和 (6) 被复制。另一方面,由于圆角的扩展,可能无法重现涉及小于 ~0.07 的小尺度的刻面。
初始形态和模拟设置
为了通过本节中定义的相场模型研究任何形态演化,φ 的适当初始条件 必须设置。我们在这里考虑在 (001) 平面上雕刻的光滑凹坑几何,参考系设置为 \(\hat {\mathbf {x}}=\,[\!100]\), \(\hat {\ mathbf {y}}=\,[\!010]\) 和 \(\hat {\mathbf {z}}=\,[\!001]\)。特别地,我们考虑半径为 L 的圆形 (001) 表面 在高度 h 0-H , 在高度 h 处平滑地连接到周围的 (001) 平面 0. 这样的几何被设置为 φ 的初始条件 通过利用方程。 (4) 与 d (r ) 到表面的有符号距离 Γ (x ,y ) 由
定义 $$ \Gamma(x,y)=\left\{ \begin{aligned}h_{0} - &H &\qquad r \leq L \\ h_{0} - &H \exp \left[ -\frac {1}{2}\frac{|\mathbf{s}-\bar{\mathbf{s}}|^{2}}{\sigma^{2}} \right] &\qquad r> L \end {对齐} \right。 $$ (7)与 \(r=\sqrt {x^{2}+y^{2}}\) 和
$$ \mathbf{s}=(x,y), \qquad \bar{\mathbf{s}} =\frac{R}{r} (x,y)。 $$ (8)R =H /4L 被定义为纵横比参数,而 σ 是控制坑底部与其周围平坦区域之间连续连接延伸的参数。这个参数在这里设置为σ =L /2.
在图1中,φ采用的初始条件 图示。图 1a 显示了 Γ (x ,0) 具有不同 R 值的配置文件 .图1b显示了φ的定义 通过等式。 (4) 在 3D 平行六面体域中。特别是,该面板显示了穿过整个域中心的横截面。左边是固相对应的区域,即φ>0.5,显示对应于初始凹坑形态的表面。右边部分说明了φ的值 在整个 3D 域中,即在体相中以及它们之间的连续过渡中。
<图片>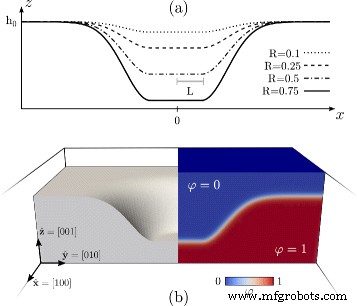
相场模型的初始条件,类似于固体薄膜 (001) 表面的光滑凹坑。 一 Γ (x ,0) 来自等式的配置文件。 (7) 针对不同的 R 获得 值。 b φ的定义 在用于数值模拟的 3D 域中。它是从方程中获得的。 (4) 与 d (r ) 到 Γ 的有符号距离 (x ,y ) 与 R =0.5。在左边,固相 φ> 0.5 显示。在右侧,显示 φ 的颜色图 在3D领域被报道
进行数值模拟以积分方程。 (2)和(3)。它们是通过使用有限元方法 (FEM) 工具箱 AMDiS [47, 48],在接口 [33, 38, 49] 处采用半隐式集成方案和网格细化来执行的。沿\(\hat {\mathbf {x}}\) 和\(\hat {\mathbf {y}}\) 方向设置周期性边界条件。无通量 (Neumann) 边界条件沿 \(\hat {\mathbf {z}}\) 方向设置在模拟域的顶部和底部。进化的时间尺度按因子 1/D 缩放 , 对应于集合 D =1。在下文中,我们以任意单位表示模拟时间。坑的大小任意设置为L =1,而界面厚度设为ε =0.2.
结果与讨论
Si(001) 凹坑的平滑
在本节中,我们将说明有关凹坑图案 Si(001) 衬底演化过程中形态变化的结果。上述模型允许通过“各向异性表面能”部分中各向异性表面能的定义来描述硅的具体情况。我们希望从定性的角度来看以下结果对于任何尺寸都是有效的,前提是系统足够大以采用连续方法 (\(\gtrsim 10\) nm) [32] 并且形状可以参数化为纵横比 R 类似于图1a。可以通过设置L来考虑实际长度比例 参数以实数单位表示,L r .然后可以通过考虑 D 的实际值来描述实时尺度 和 γ 0 并乘以 L r 长度,即通过 L 缩放 r /L 与 L 如上所述的幺正。
让我们首先关注进化的第一阶段。由方程设置的初始条件。 (7) 由不表现出任何表面优先取向的轮廓组成。当考虑由各向异性表面能降低驱动的表面扩散演变时,预计初始轮廓的刻面。这在图 2 中说明,其中带有 R 的两个轮廓的刻面 =0.25 在图 2a 和 R 报道了图 2b 中的 =0.5。色标说明了表面上的值 \(\gamma (\hat {\mathbf {n}})\)。这允许将面识别为具有几乎均匀的表面能密度的区域,对应于方程的最小值。 (5),由具有高值 \(\gamma (\hat {\mathbf {n}})\) 的局部区域限定。根据凹坑的初始纵横比,形成不同的刻面。对于较小的 R,底部的 (001) 小平面保持为方形。凹坑的边缘由四个 {113} 小平面包围,这些小平面由小的三角形 {110} 小平面连接。根据较大的纵横比,考虑 R 时存在较大的刻面 =0.5,允许出现相对于 (001) 表面具有更高斜率的优先取向。特别是,初始形状允许在靠近底部和平坦区域的两个 {113} 面之间形成 {111} 面。在两者之间,形成了宽{110}面。
<图片>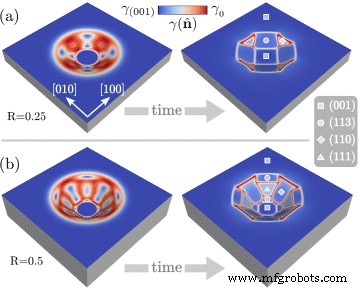
根据表面扩散和 \(\gamma (\hat {\mathbf {n}})\) 再现 Si 的表面能,对“初始形态和模拟设置”部分中定义的初始轮廓进行刻面。考虑了两种不同的初始形态:a R =0.25 和 b R =0.5。在刻面形态上,采用符号来标识刻面族。色标显示\(\gamma (\hat {\mathbf {n}})\) 在表面的值
图 2 中报告的结果显示了根据纵横比或通常根据初始形态预测刻面凹坑形态的可能性。我们现在还研究了长期尺度动力学,检查形态演化直至达到平衡 [38]。这在图 3 中进行了说明,其中我们专注于迄今为止考虑的最深坑,即 R =0.5,显示主要形态变化。特别是,在进化过程中获得的不同形态的透视图和俯视图分别报告在图 3a、b 中。在这个模拟的第一阶段,我们观察到最陡峭的 {111} 面的消失和相邻的 {113} 面的扩大。然后,后者合并,{110} 面开始收缩。发现这些在呈现三角形后在后期阶段消失,从顶视图给坑提供方形轮廓。此外,{113} 面最终会消失并实现全局扁平化。在这个模拟中获得的实时尺度可以用文献中的数据来估计。特别是,我们可以考虑 D 由阿伦尼乌斯定律确定,前因数和活化能来自参考文献。 [50],其中也考虑了热波动。 γ 0 设置为 \(\gamma (\hat {\mathbf {n}})\sim 8.7\) eV/nm 2 当 \(\hat {\mathbf {n}}=(001)\) [51] 从方程。 (5),即γ 0=10.2 eV/nm 2 .其他与材料相关的表面扩散系数 [28],即表面的原子体积和密度,被设置为重现 Si 的情况。根据这些值,对于 L,整个过程在高温 T ∼1100−1200 °C 下的预期持续时间 r 几十纳米是几个小时的数量级。
<图片>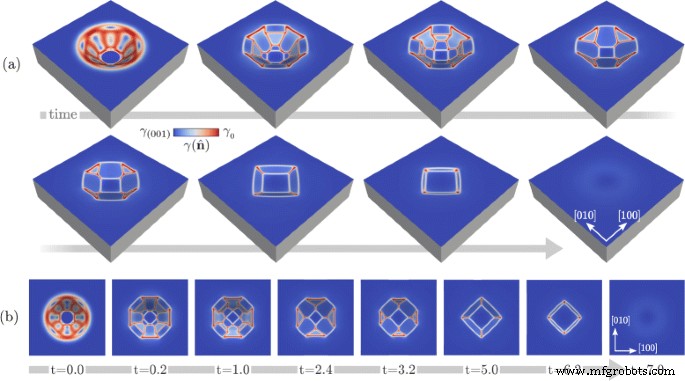
具有如图 2b 所示的初始形态的 Si 坑向平衡演化。 一 显示主要形态变化的透视图。 b 面板 a 中形态的顶视图 .面板 b 中报告的时间 以任意单位表示。色标显示\(\gamma (\hat {\mathbf {n}})\) 在表面的值
随着进化过程中发生的特定形态变化,应注意两个主要特征。首先,演化导致表面预期的整体变平,这发生在陡峭的刻面逐渐消失被较浅的刻面取代。虽然这种行为可以仅通过关于能量最小化和降低纵横比的论点来推断,但值得指出的是,这里提供了完整的演变,处理了相似面但具有不同相对尺寸的存在。这与在演化过程中获得的形态对应于非平衡配置并定义了一条通向全球能量最小值的路径这一事实是一致的。然后,尽管预期的方面及其能量学是已知的,但只能通过考虑动力学而不是仅通过考虑全局能量最小化来描述特定演化点的特定形态 [38]。
图 3 中报告的结果显示的第二个重点是关于中间阶段。当演化过程中的形状接近深度类似于使用 R 获得的初始轮廓的几何形状时 =0.25,即在 t ∼3.2,由能量最小化引起的形态与图 2b 中报告的非常相似,即使从具有显着深度差异的初始配置开始(在这种情况下为两倍)。这表明存在通向最终平坦化的共同动力学途径,这是在初始形态的第一次快速刻面之后达到的。这个论点实际上在图 4 的图中得到了证实和进一步说明。这里,当考虑带有 R 的凹坑时,报告了初始刻面后演化过程中的单调能量衰减 等于 0.1、0.25、0.5 和 0.75,如图 1a 所示。在图 4a 中,考虑了以任意单位表示的时间尺度。在图 4b 中,随着时间尺度的适当移动,报告了相同的能量变化,突出了接近结构的相似纵横比时相似的能量衰减。 \(t^{*}_{R}\) 定义为获得平面的时间,即达到全局能量最小值的时间,如图 3 所示,每次模拟都不同。 4 一个。如该图所示,R 的能量衰减几乎重叠 ≤0.5。仅在考虑 R 时才观察到非常小的差异 =0.75,其能量衰减结果仍然非常接近其他曲线,对于\(t \gtrsim 5.0\),差异基本消失。值得一提的是,对于与初始配置有较大偏差的情况,即使用 R ≫1,这些几何形状可能会随着时间尺度和形态的不同影响而不同地演化 [52, 53]。此外,已知在极端情况下会发生拓扑变化,例如非常深的沟槽,阻止了在平坦的 (001) 表面上达到全局平衡的可能性 [34, 39, 54]。
<图片>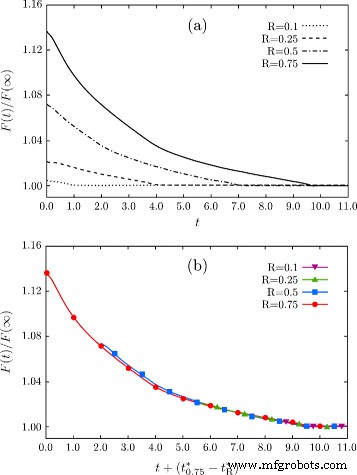
在凹坑几何形状的演变过程中能量下降。 一 F (t ) 由作为演化最后阶段获得的平坦 (001) 表面的能量归一化。从具有不同 R 的模拟中获得的能量衰减 对于初始配置文件,即来自 R =0.1 到 R =0.75,如图所示。时间以任意单位表示。 b 曲线如面板 a 移位以匹配 \(t_{R}^{*}\),即根据 R 实现凹坑全局平坦化的时间
在这些部分报告的模拟中获得的形状有望在实验中观察到,特别是当加工涉及接近热力学极限的条件时。图 3 中报告的一些形态实际上确实对应于凹坑图案的 Si(001) 衬底的轮廓。例如,由宽 (001) 表面构成的形态由窄 {113} 小面包围,如图 3 中 t 当考虑纵横比为 0.05<R 的凹坑图案 Si(001) 衬底时,观察到 ~5.0 <0.1 如参考文献。 [10, 30]。此外,图 3 模拟的上述阶段中小平面的相对扩展与这些实验工作中报告的非常相似。模拟和实验之间的这种一致性进一步评估了此处采用的表面扩散的理论描述。然而,我们专注于该过程的一般特征,与具体实验进行更详细的比较超出了当前工作的目的。
模仿 Ge 过度生长导致的形状变化
正如介绍中提到的,凹坑图案 Si 模板的主要应用之一是控制自组装岛的生长 [55]。这在考虑 Ge 或 Si1 - c 的位置时尤其适用 Ge c Si(001) 衬底上的岛 [6]。使用上一节中采用的方法,我们可以检查与表面能的特殊特征相关的形态变化。因此,通过从类似于 Si 坑的真实形态的适当初始配置开始,并考虑沉积另一种材料时预期的表面能密度差异,我们可以预测对形态变化的相应贡献。
案例研究包括在纵横比接近 0.1 的 Si(001) 凹坑图案衬底上 Ge 的过度生长。图 3 在 t 处的轮廓 =5.0 被认为是初始形态。然后,设置还包括沿<105>方向的最小值的表面能。 \(\gamma (\hat {\mathbf {n}})\) 的这个定义模拟了 Ge/Si(001) 系统中最喜欢的小斜率取向的存在 [56-58]。 {105} 面的高稳定性是由于表面重建和与外延层和衬底之间的晶格失配相关的应变效应之间的相互作用 [59-61]。必须在方程中使用的表面能密度值。 (6) 取自参考文献。 [58] 在一个厚的 Ge 层的极限。请注意,此处忽略了表面能更接近 (001) 的其他面,例如 {1 1 10}。由于<105>和[001]方向之间的夹角非常小,w 我 需要比以前采用的参数更大的参数来正确描述方程的能量最小值。 (5) [38]。特别地,我们设置 w {105}=w {001}=500。
在图 5 中,报告了具有 \(\gamma (\hat {\mathbf {n}})\) 新定义的表面扩散演化。图 5a 显示了表面的形态演变,放大了 z -轴乘以因子 5。在第一阶段,{105} 面在初始轮廓中存在的 {113} 面之间形成。由于〈105〉取向的能量最小,如图 5b 所示,相应的小面延伸而 {113} 小面收缩。在后期阶段,以 {105} 面为边界的凹坑仅在底部形成(001)表面。从图 5b 中的俯视图来看,形态的变化导致凹坑轮廓旋转 45°。这实际上是在实验中在硅图案基板上沉积 Ge 期间观察到的 [41],或者在由于缺陷或杂质引起的凹坑自发生长期间 [40]。还发现 {105} 面的形成是 Ge 点进一步生长的最佳成核位点 [30]。图 5 中所示的演变表明,仅由于表面能降低,可以实现导致凹坑轮廓旋转的形状变化。预计这将是接近平衡条件下的真实情况,当热力学驱动力由表面贡献主导时,即对于小 Ge 体积。实际上,为了充分描述该过程,必须包括弹性效应、混合和固相的生长[32]。还值得一提的是,实验中采用了更浅的 Si 坑,显示了沿 {11n 的法线的小平面 } 方向,有 5<n <10 [41](即 {1 1 10} 面)。以这些面为界的凹坑几何形状将导致类似的演变,因为它们对应于图 4 中采用的初始配置,只是相对于 (001) 平面的斜率较小。
<图片>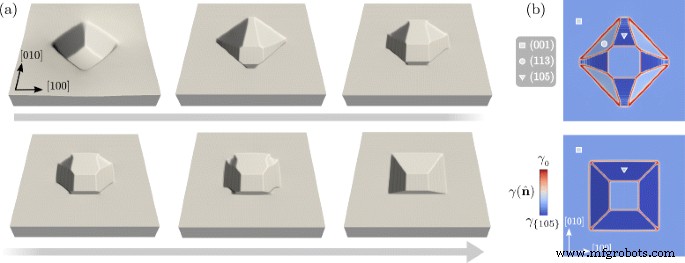
图 3 中 t 中轮廓的演变 =5.0,表面能的定义包括<105>取向。 一 向形成仅由 {105} 面限定的凹坑的演化的代表性阶段的表面轮廓。 z -axis 放大 5 倍。b 显示表面的 \(\gamma (\hat {\mathbf {n}})\) 值的顶视图。 a面板的第二个和最后一个阶段 分别在顶部和底部报告。采用图2中的符号来标识不同的刻面族
结论
在这项工作中,我们使用基于表面扩散的连续模型来研究在 Si(001) 衬底中挖掘的凹坑的时间演变。通过适当地解决(强)表面能各向异性问题,使用基于众所周知的 Si Wulff 形状的参数化,我们预测了与实验一致的典型亚稳态配置,包括不同材料的沉积引入新稳定面的情况。已经说明了凹坑整体变平的整个演变过程,并且在考虑具有不同初始深度的凹坑时,发现它也遵循相同的动力学路径。 We believe that the model can be predictive also for initial configurations strongly deviating from the ones which we have analyzed as examples. As a consequence, the present approach can be useful in designing experiments based on still-unexplored pit shapes. Furthermore, the model is general and can be easily adapted to different substrates upon re-parametrizing the surface energy.
纳米材料


