基于分数阶微分方程的超级电容器储能估算
摘要
在本文中,介绍了仅使用超级电容器端子上的电压测量来估计累积能量的新结果。为此,基于超级电容器充电/放电电路的分数阶模型的应用进行了研究。然后使用模型的参数估计来评估超级电容器中累积的能量量。将获得的结果与通过测量超级电容器端子上的电压和电流通过实验确定的能量进行比较。对各种输入信号形状和参数重复所有测试。估计和实验结果之间的高度一致性充分证实了所提出的方法的适用性,从而证明了分数阶微积分在超级电容器储能建模中的适用性。
背景
迄今为止,超级电容器是许多设备和系统的主要组件,例如备用电源和电力回收系统以及汽车应用、混合动力汽车等。与典型电池相比,无需任何化学反应即可积累电荷的能力使此类元件的充电/放电循环次数高出数百倍 [1]。此外,高充电/放电率使它们在能量回收系统中的应用非常有效,例如用于运输或可再生能源 [2, 3]。在所有这些应用中,关键参数是关于超级电容器中累积能量的信息 [4, 5]。不幸的是,典型电容器的众所周知的关系可以确定信息,即 (1/2)C U 2 , 不能使用 [6]。不能仅根据电容器端子上的电压来确定累积能量的大小。造成这种情况的主要原因是与电荷重新分布相关的扩散过程 [1, 7]。这就是为什么许多研究人员一直试图确定一个超级电容器模型,以评估真实系统的行为。目前,研究人员主要采用典型电子元件的组合,例如RC 四极或此类元件的串联和并联组合。然而,所有这些模型都以典型的整数阶微分方程[3-5, 7]的形式假设了超级电容器电流与其终端电压之间的关系。
但事实证明,通过应用分数阶微积分,可以获得在此类系统中进行能量估计的一些全新的可能性 [8, 9]。非整数阶微分积分微积分是在 300 多年前提出的,但重要的实现问题与计算机的出现及其在离散时间动态系统建模中的使用有关 [10-14]。将分数阶微积分应用于超级电容器参数估计问题并不是一个新问题。该领域有许多出版物[15-25]。作者在频域和时域中执行估计参数的任务[26]。
本文是作者会议报告 [27] 的扩展版本,其中简要介绍了分数阶方法来估计超级电容器中累积的能量。
超级电容器参数的准确估计对于评估其可靠性也至关重要 [28-31]。超级电容器内部的永久退化过程会改变等效串联电阻和电容。因此,基于所提出的方法准确确定这些参数也可以准确评估电容器的性能。
本文首先介绍了与分数阶积分和微分相关的一些预备知识。接下来,介绍了试验中使用的参数估计方法,并提出了基于分数阶微积分的能量计算新方法。结果和讨论部分介绍了各种场景的计算能量,并将它们与参考(测量)值进行比较。结论和贡献总结在结论部分。
方法
超级电容器中多孔材料的使用和电荷积累的特定方式导致基于整数阶导数模型的传统方法不够准确。许多研究人员以典型的RC的组合形式提出了各种解决方案。 具有常量或变量值的元素 [4, 7]。但事实证明,使用非整数阶微分演算来定义超级电容器的电流和电压之间的关系,肯定可以获得更好的精度 [17, 19]。此外,这样的解决方案可能会导致非常简单的模型结构,同时提供非常高的精度[18]。
分数阶微分-积分微积分
分数阶微分已经为人所知 300 多年。然而,仅在最近几年,它才在物理现象和过程的建模中流行起来。人们相信,用非整数阶的导数或积分来描述动力学是对许多复杂现象和工业过程的真实属性进行建模的最有效方法之一,尤其是基于新材料和技术 [10, 12, 13] , 32–34]。
非整数阶微分或积分微积分是经典微积分对α阶的推广 属于实数集\(\mathcal {R}\)。函数 f 阶 \(\alpha \in \mathcal {R}\) 的微分-积分算子 (t ) 范围 [a ,t ]可以写成如下
$$ {{}_{a}\mathcal{D}_{\textit t}^{\alpha}}f(t)=\left\{ {\begin{array}{lcl} {\frac{\mathrm {d}^{\alpha}\textit{f(t)}}{\mathrm{d} \textit{t}^{\alpha}}} &\text{for} &\alpha>0\\ f( t) &\text{for} &\alpha=0\\ \int_{a}^{t} f(\tau)\textrm {d} {\tau^{\alpha}} &\textrm {for} &\alpha<0,\\ \end{array}} \right。 $$ (1)假设函数 f (t ) 是多次可微和可积的。对于算子(1),其实现有多种定义。这些定义在特性和应用领域上有所不同。最受欢迎的是 Riemann-Liouville、Caputo 和 Grünwald-Letnikov (GL) 定义 [34]。后者将在本文中以
的形式使用 $$ {}_{a}\mathcal{D}_{t}^{\alpha} f(t) ={\lim}_{h \to 0} \frac{1}{h^{\alpha} } \sum\limits_{j=0}^{\left[{\frac{t}{h}}\right]}(-1)^{j}{\alpha \choose j}f(t-jh) , $$ (2)其中二项式 \(\alpha \choose j\) 定义如下
$$ {\alpha \choose j}=\left\{ \begin{array}{lll} 1 &\textup {for} &j=0 \\ \frac{\alpha (\alpha-1) \dots (\alpha -j+1)}{j!} &\text{for} &j>0。 \end{array} \right。 $$ (3)为了得到离散时刻的分数模型,将离散形式的GL定义简化为
$$ \Delta_{h}^{\alpha} f(t) =\frac {1}{h^{\alpha}} \sum\limits_{j=0}^{t}(-1)^{j }{\alpha \选择 j}f(tj)。 $$ (4)GL 方程有几种离散化方案。 (4).最受欢迎的包括向后差分 (Euler)、梯形 (Tustin) 和 Al Alaoui 算子。使用欧拉方法,离散时刻k的分数阶导数 可以表示为
$$ \Delta_{h}^{\alpha} f(k)=\frac {1}{h^{\alpha}}\sum\limits_{j=0}^{k}(-1)^{j }{\alpha \choose j}f(kj),\; k=0,1,\ldots。 $$ (5)由于有限的内存和有限的计算时间,先前样本的无限总和必须在实际系统中限制为有限值。现在,GL 的截断或有限长度离散时间近似为
$$ \Delta^{\alpha} f(k) =\frac {1}{h^{\alpha}}\sum\limits_{j=0}^{L}(-1)^{j}{\ alpha \选择 j}f(kj),\; k=0,1,\ldots, $$ (6)其中 f (l )=0 对于 l <0 和 L 是模型 (6) [23] 的长度。减少样本数量会导致计算精度降低。这对于连续运行的系统很重要。其他一些解决方案是用整数阶模型逼近分数阶微分积分的算法。一个例子可以是 Oustaloup 递归过滤器 [35]。另一个有效的有限长度模型是 FFLD,它是截断模型 (6) 和基于 Laguarre 的差异 [24, 36, 37] 的组合。
所有识别结果和能量测量结果均基于(长)观察窗L中的所有样本获得 ,即以最大的精度。图 1 给出了基于(6)获得的积分和微分的阶跃响应,对于 k =0,1,...,L 以及积分/微分阶α的各种值 .假设 α 阶的不同值 ,可以更准确地模拟不同的物理过程,尤其是扩散过程。
<图片>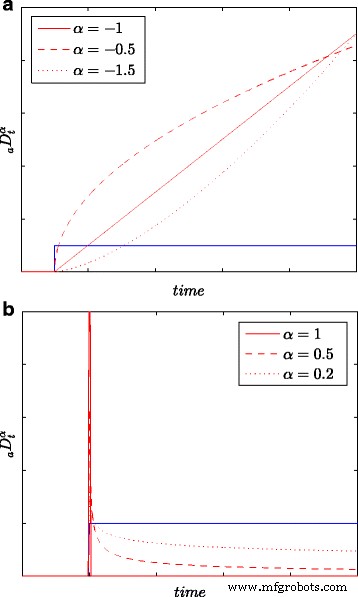
积分阶跃响应 (a ) 和区分 (b ) 不同阶数的模型 α
分数模型的参数估计
本文中介绍的所有能量测量和识别程序的结果都是针对从受控电压源充电的超级电容器获得的。在这样的系统中,超级电容器电流 i C (t ) 必须由电阻 R 限制 与超级电容器C串联 (图2)。所有超级电容器参数的估计基于四极响应u C (t ) 到电压阶跃 u (t ) 在其输入处。选择合适的导数阶α值 允许解释与充电和放电过程中与电荷重新分布相关的扩散过程相关的物理现象的超级电容器模型。并联电阻r P 此外,还可以对漏电流进行建模。使用分数阶微分对超级电容器建模,模型结构可以具有低复杂性。对于从电压源充电的超级电容器,模型仅包含两个元素,即一个简单的 RC 四极杆(图 2a)。对于低容量,串联电阻 r S 很重要(图 2b),而漏电流 I L 还可以由并联电阻 r 表示 P (图2c)。使用分数阶微积分对超级电容器进行建模,电容器端子上的电压与其电流之间的关系可以表示如下
$$ i_{C}(t)=C_{\alpha}\frac{\mathrm{d}^{\alpha} u_{C}(t)}{\mathrm{d} t^{\alpha}}, $$ (7)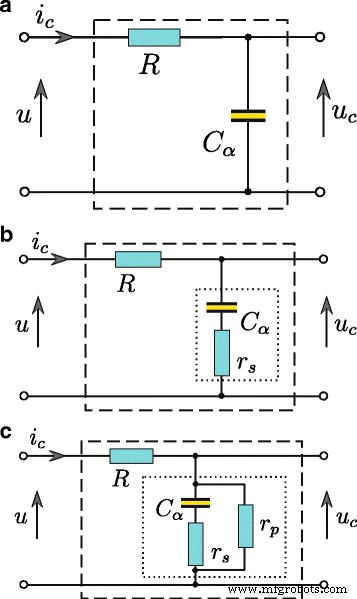
超级电容器RC 模型,基本模型 (a ),扩展为串联电阻 (b ),并带有额外的并联电阻 (c )
其中操作符 d α /dt α 表示α阶微分算子 和 C 的 SI 单位 α 是 [F/sec 1−α ]。图 2a 所示的基本超级电容器配置可以视为一阶惯性系统,可以用分数传递函数表示
$$ G(s^{\alpha})=\frac{U_{C}(s)}{U(s)}=\frac{1}{Ts^{\alpha} +1}, $$ (8 )其中 T =R C α .考虑串联电阻r S (图2b),电路被视为具有传递函数的相位延迟校正系统(比较[24])
$$ G(s^{\alpha})=\frac{1}{T_{1}s^{\alpha}+1}+\frac{T_{2}s^{\alpha}}{T_{1 }s^{\alpha}+1}, $$ (9)其中 T 1=C α (R +r S ) 和 T 2=r S C α .此外,允许并联电阻 r P 表示漏电流I L (图2c),系统传递函数可以表示为
$$ G(s^{\alpha})=\frac{T_{2}s^{\alpha} +1}{T_{1}s^{\alpha} +K}, $$ (10)其中 K =R /r P +1,T 1=C (R r s /r P +R +r S ) 和 T 2=r S C .在时域中,方程。 (10) 可以表示为
$$ \frac{\mathrm{d}^{\alpha} u_{C}(t)}{\mathrm{d}t^{\alpha}}=\frac{1}{T_{1}}(u (t)-Ku_{C}(t))+\frac{T_{2}}{T_{1}}\frac{\mathrm{d}^{\alpha} u(t)}{\mathrm{d }t^{\alpha}}。 $$ (11)由(11)定义的模型的时间响应是通过将其转换为图 3 中以图形方式呈现的形式获得的,其中积分和微分运算是分数阶α .在估计超级电容器参数的过程中使用了该模型。使用图 4a 中所示的系统识别测试的超级电容器。整个系统的控制程序是使用带有xPC Toolbox 的Matlab/Simulink 软件开发的。该系统由安装有测量卡 NI-DAQ 的台式 PC(xPC Target)和主计算机(xPC Host)组成。计算机通过以太网互连。超级电容器由(电压控制的)电压源(图 4b)充电和放电,电流效率高达 ± 3 A。测量系统以 100 Hz 的采样频率运行,而所有测量和模拟控制信号均为以 16 位分辨率处理 [25]。
<图片>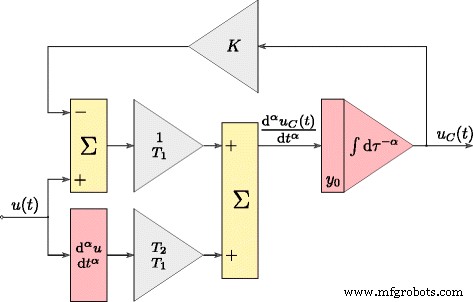
时域超级电容器模型的Matlab结构
<图片>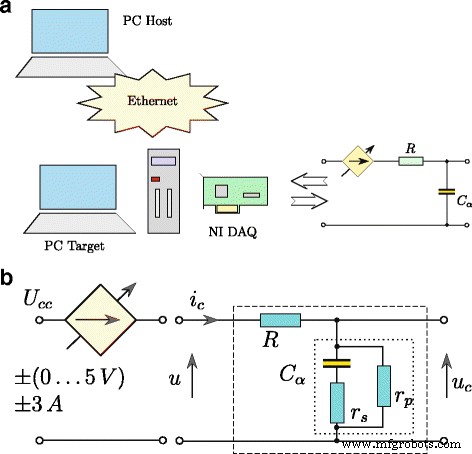
测量系统的结构 (a ) 和超级电容器充电/放电方案 (b )
确定系统动态特性的主要方法是基于阶跃响应的分析 [38]。关于系统模型,该方法允许估计其参数。在本研究中,使用了具有各种电压 (0.5/1.0/1.5/2.0/2.7 V) 和恒定持续时间 (500 s) 的阶跃信号(见图 5 和表 2)。另一方面,超级电容器的典型应用之一是将能量积累或输送到电力系统中。在这种情况下,电压变化率相当小。为了模拟它,使用了 400 mVpp 和 0.03 rad/s 的 2 V 偏移信号(图 6)。此外,为了检查电压和频率变化对估计参数的影响,使用了后者的各种值(见表 3)。
<图片>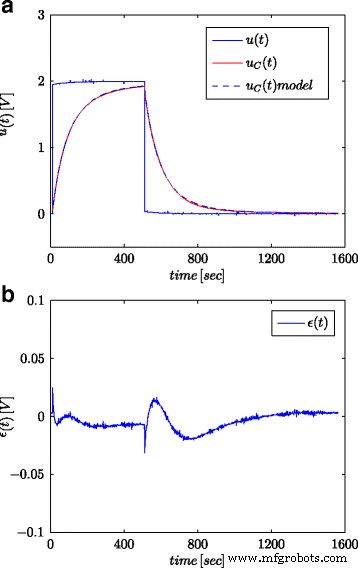
测试超级电容器的阶跃响应及其分数模型 (a ) 和模型响应误差 (b )
<图片>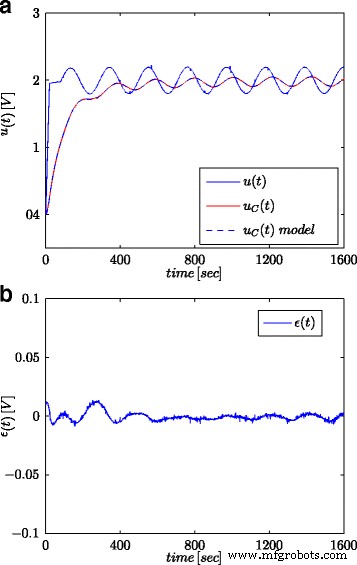
被测超级电容器的正弦波响应及其分数模型 (a ) 和模型响应误差 (b )
有几种估计模型参数的方法。在这项工作中应用的时域识别程序的主要目的是估计未知参数的向量θ =[α ,C α ,r S ,r P ] 由(11)提出的分数模型。最小二乘法用于最小化初始误差。优化准则涉及标准误差\(\|\epsilon (k)\|_{2}^{2}\) 的最小化,其中
$$ \epsilon(k)=u_{C}(k)-\hat{u}_{C}(k), $$ (12)其中 u C (k ) 是被测系统在 k 时刻测得的输出电压 , 而 \(\hat {u}_{C}(k)\) 是输入信号 u 所考虑模型的输出电压 (k )。识别问题现在简化为寻找参数向量θ ∈Θ 广告 这将最小化平方标准 J 以这样的方式
$$ \min_{\theta\in\Theta_{ad}} \left\{ J=\sum_{0}^{N} {\epsilon(k)^{T}\epsilon(k)}\right\} , $$ (13)其中Θ 广告 表示一组可接受的参数值和 N 表示模拟时间。有许多优化算法可用于解决问题 (13)。本文的结果是通过在Matlab环境中实现遗传算法获得的。
能量计算
超级电容器中储存的能量的变化取决于单位时间内提供给电容器的功率,可以描述如下
$$ \mathrm{d}E(t) =P(t)\mathrm{d}t。 $$ (14)通过将提供给电容器的功率表示为电容器端子上的电流和电压的乘积,在给定时间 t 的能量变化 可以表示为
$$ \mathrm{d}E(t) =u_{C}(t)i_{C}(t)\mathrm{d}t。 $$ (15)时间间隔 [t 内的总能量 1,t 2] 可以通过对这段时间内的能量变化进行积分来获得
$$ E_{tot}=\int_{t_{1}}^{t_{2}}\mathrm{d}E(t)=\int_{t_{1}}^{t_{2}}u_{C }(t)i_{C}(t)\mathrm{d}t。 $$ (16)会计等式。 (7)、总能量存储可确定为
$$ E_{tot}=C_{\alpha}\int_{t_{1}}^{t_{2}}u_{C}(t)\frac{\mathrm{d}^{\alpha} u_{C }(t)}{\mathrm{d}t^{\alpha}}\mathrm{d}t。 $$ (17)假设 t 1=0且\(E_{t_{1}}=0\),超级电容器在[0,t时间段内储存的总能量 ] 是
$$ E(t)=C_{\alpha}\int_{0}^{t}u_{C}(\tau)\frac{\mathrm{d}^{\alpha} u_{C}(\tau) }{\mathrm{d}\tau^{\alpha}}\mathrm{d}\tau. $$ (18)注意对于 α =1 方程(18) 可以简化为经典的
$$ E(t)=\frac{1}{2}Cu_{C}(t)^{2}。 $$ (19)结果与讨论
最初,执行使用分数微积分估计超级电容器模型的参数向量的过程。估计是基于图 2c 中所示的系统进行的,在其输入处生成电压阶跃或正弦波。基于 (11) 计算模型响应。两种识别程序得到的结果非常相似,尤其是在分数电容C的情况下 α 和分数阶α (见表 1)。串联电阻r估计的一些差异 S 可能是因为它依赖于频率。阶跃信号由许多高频谐波组成,而正弦波只有一个 - 0.03 rad/s。所呈现的结果是针对商用超级电容器 Samwha Green–Cap EDLC(DB) 获得的,额定电压为 2.7 V,具有 100 F 标称电容和 8 mΩ 最大等效串联电阻 (r S ) 1 kHz。
图 5a 和 6a 分别显示了测量的超级电容器电压和计算的模型响应,分别针对阶跃和正弦信号,而图图 5b 和 6b 显示了模型响应误差。
尽管提出了相对简单的模型,但所有获得的结果都显示了模型响应和实际测量值之间的高度一致性。一些差异可能是由于模型参数应该在使用电流源的超级电容器充电和放电系统中估计的事实 [25]。此外,对 r 的估计非常高 P 可能表明该电阻可以从图 2c 所示的超级电容器模型中排除。那些非常高的估计值及其对不同输入的高差异表明用于估计此参数的测试信号不正确。模型 (10) 被用作最通用的形式。但是,为了准确确定其所有参数,必须使用其他程序和测试信号。 r 的值 P 表征漏电流I L 并且应该使用恒压信号来确定,但是需要很长时间——几十个小时的量级。
尽管该研究的主要目标是测量能量,但各种激发条件在很大程度上影响了所有参数估计(见表 2)。例如,电压阶跃幅度的增加显着改变了分数积分阶数,这是超级电容器内部扩散现象的增加效应的结果。从表 2 还可以看出,超级电容器是非常非线性的。作为积分阶数变化的结果,也观察到分数容量的变化。这也适用于正弦激励。估计参数的值——尤其是α 和 C α ——取决于幅度和频率(见表 3)。对于低频,幅值很重要,而对于高频,超级电容器的行为就像被恒压激励一样。
能量计算
图 7a 和 8a 显示了图 4b 所示配置的超级电容器的电压和电流的测量值。这些值用于计算存储在电容器中的总能量(标记为 E 图中的 1 7b和8b)根据(16)。正如参数识别过程一样,计算是针对系统输入端的电压阶跃和正弦波进行的。每次t以这种方式计算的能量 与根据 (19) 的电压和容量计算的能量进行比较(标记为 E 图 3 中。 7b 和 8b) 和用分数阶微积分计算的能量(标记为 E 2 图中7b和8b)根据(18)。对于方程。 (19),采用了超级电容器的标称值(C n ),而在 (18) 中,使用了从表 1 中给出的估计过程中获得的值。图 7b 显示了电压阶跃的测量和能量计算结果,而图 8b 显示了与正弦波相同的量。对不同的电压阶跃和正弦激励进行了类似的计算。图 9a、b 分别显示了两个电压阶跃 0.5 V 和 2.7 V 的测量和计算能量示例。图 10 显示了频率为 0.03 rad/sec,不同幅度为 0.1/0.25/0.5 和 0.7 V 的正弦信号的能量变化。可以看出,确定的能量值的差异对应于估计值的差异分数阶α .与值− 1 的差异越大,计算的能量差异越大。
<图片>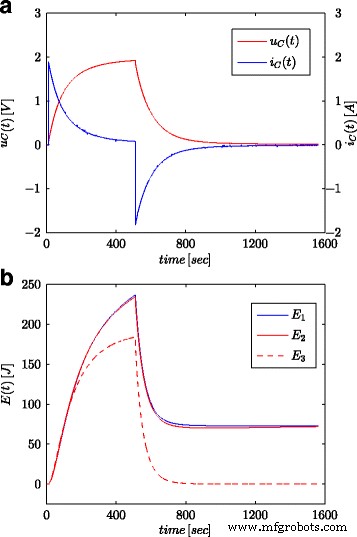
超级电容器电压和电流的阶跃响应 (a ) 和计算的能量值 (b )
<图片>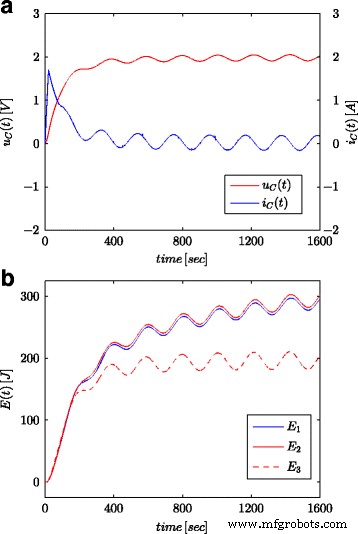
超级电容器电压和电流的正弦响应 (a ) 和计算的能量值 (b )
<图片>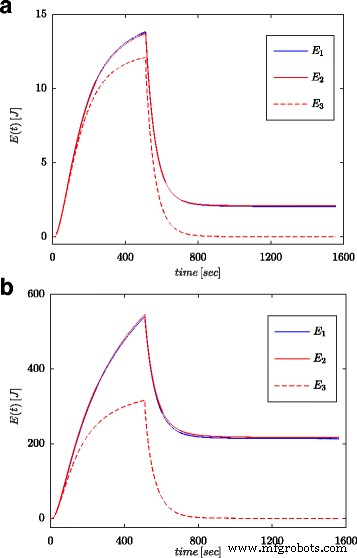
为 0.5 V (a ) 和 2.7 V (b )
<图片>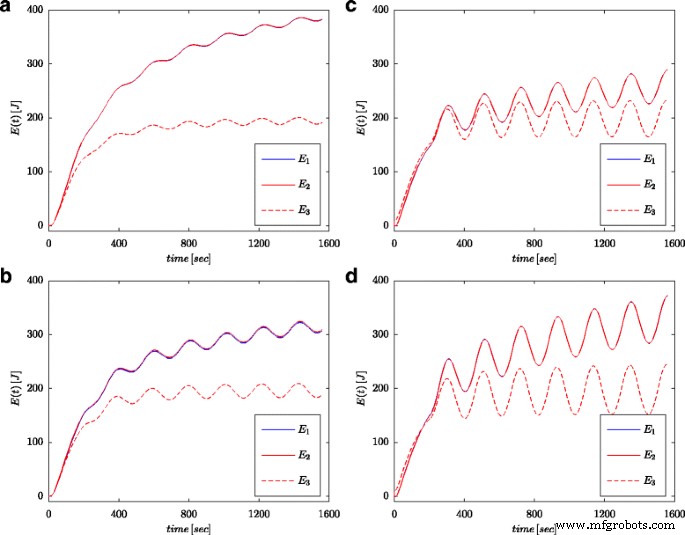
为频率为 0.03 rad/s 且振幅为 0.1 V (a ), 0.25 V (b ), 0.5 V (c ) 和 0.7 V (d )
讨论
在超级电容器中使用活性炭形式的多孔材料电极,由非常薄的隔膜隔离,并使用电荷积累机制作为所谓的双层,从而极大地提高了它们的容量。然而,新材料和新设计解决方案的应用导致整数阶导数和积分形式的传统数学计算显得不准确。传导测量和计算证明了超级电容器的分数阶性质。通过正确估计非整数阶α 微分/积分,我们可以使用简单的数学模型精确地模拟超级电容器内部发生的现象和过程。
考虑到由(16)确定的累积能量的实际值,具有标称参数的整数阶模型(19)低估了能量的数量,而分数模型(18)表明几乎相同的值。
执行的测试和测量与超级电容器通过电压源的充电和放电有关。在工业条件下,超级电容器通常通过电流源进行充电和放电。这会改变系统的性质,因为电容器不再是惯性系统,而是成为典型的积分系统。然而,作者进行的测量也表明在这种情况下会发生扩散过程。无论如何,这里确认了 Gründwald-Letnikov 导数/积分的有用性。另一个问题与 GL 微分积分算子的实现有关,例如有限或截断的 GL 差值 (6),这可能在计算上很繁重。在未来的研究中,我们将比较 Oustaloup [35] 和 FFLD [24, 36, 37] 逼近器,以有效解决实现问题。
仅根据超级电容器端电压的测量值计算超级电容器的储能量并使用模型(19)是不合适的。只有当电容器电流由电容器电压的整数阶导数表征时,模型(19)才有效(i C (t )=du C (t )/dt )。由于其结构和使用的特殊材料,超级电容器并非如此。然而,同样的问题发生在由电流源充电的非常大的超级电容器上。超级电池也有相当新的元素。在所有这些应用中,由于这些元件的特定属性,电流变化不以端电压的整数阶导数为特征。
结论
在本文中,提出了一种估算超级电容器中累积能量的新方法。分析是利用分数阶模型的某些独特属性进行的。已经表明,应用这种复杂的建模会导致非常准确的结果,即使模型本身并不具有很高的复杂性,也可以获得这些结果。这是由于非整数阶动力学具有模拟扩散过程的自然能力,就像超级电容器中的电荷重新分布一样。本文的研究结果证实了超级电容器的分数性质。
纳米材料


