弹性刚度和表面附着力对纳米粒子弹跳的影响

背景

可以说，颗粒力学最基本的过程是两个颗粒的碰撞。在大颗粒速度下，碰撞后颗粒再次分离，碰撞结果可以用非弹性碰撞的经典力学来表征。然而，在小颗粒速度下，颗粒会粘住。粘连和弹跳碰撞 [1] 之间的边界可以称为弹跳速度，v b .该参数对于纳米颗粒特别重要，并且在天体物理学中具有应用，其中它进入了碰撞尘埃聚集的描述[2, 3]。

宏观接触力学已被用于推导出 v 的预测 b .它基于 Johnson-Kendall-Roberts (JKR) 理论 [4]，该理论使用弹性刚度和表面粘附力作为基本物理输入来描述两个粘附球体的碰撞。从数量上讲，这些量由压痕模量 E 描述 ind=E /(1−ν ² )，其中 E 是杨氏模量和 ν 泊松数，由表面能 γ .随着球体半径 R 和质量密度 ρ , 两个相同球体的弹跳速度为 [1, 5, 6]

常数 C 的值 强烈依赖于碰撞过程中能量耗散的假设，并且已经讨论过假设值在 0.3 和 60 之间 [1, 7]。

该预测的有效性主要针对其大小依赖性进行了研究 [1, 5-8]。随着晶粒尺寸的减小，粘附力变得更加重要，并且弹跳速度增加。事实上，对纳米颗粒（Ag 和 NaCl 颗粒）[9] 的实验发现 v b 对于几个 10 nm 的晶粒尺寸，在 1 m/s 的范围内，但对于较小的晶粒，则急剧增加。基于分子动力学 (MD) 的原子模拟证实了预测的 R ^−5/6 尺寸 R 的无定形二氧化硅颗粒之间碰撞的相关性 =15–25 nm [7]。

到目前为止，v 的预测依赖 b 关于材料参数E ind 和 γ 没有经过详细测试。这在实验中并不容易完成，因为不同的材料通常在两个数量上都不同。然而，使用 MD，我们可以构建模型材料，它们具有相同的特性，但仅在一方面不同，要么 E ind 或 γ .在本文中，我们为 Cu [10] 选择了一个模型，但将材料参数与实际值相差一个数量级。由于我们在该系统中没有发现非晶纳米粒子的弹跳，因此我们将重点放在结晶 (fcc) 晶粒上。

方法/实验

我们使用莫尔斯势，

描述距离 r 的两个原子之间的相互作用 .三个莫尔斯参数 D , α , 和 r 0被确定来描述晶格常数a , 体积模量 B , 和内聚能 E 块状 fcc 固体的 coh。

为了确定性，我们将晶格常数固定为 a =3.615 Å（适用于Cu）在本研究中也采用Cu的原子质量，以保持质量密度ρ 在方程式中(1) 固定。电位在 r 处截止 c =2.5a;因此，12 个相邻壳层，包括总共 248 个原子，与每个原子相互作用。为 B 评估了 100 个电位 在 403 到 1008 GPa 的范围内，以及 E coh 在 0.35 到 3.54 eV 的范围内。请注意，这里研究的体模量更大，内聚能更小，比真正的 Cu (B =134.4 GPa，E coh=3.54 eV [11])，因为对于实际值，我们没有观察到任何反弹。

我们确定压痕模量 E ind 从杨氏模量和该方向的泊松数 ([12], p. 32) 中的 (100) 方向的单轴应力。图 1a 显示了 E 的依赖 在 B 上找到 .我们看到这些量服从线性关系；在恒定体积模量下，内聚能的降低使 E 指数增加。

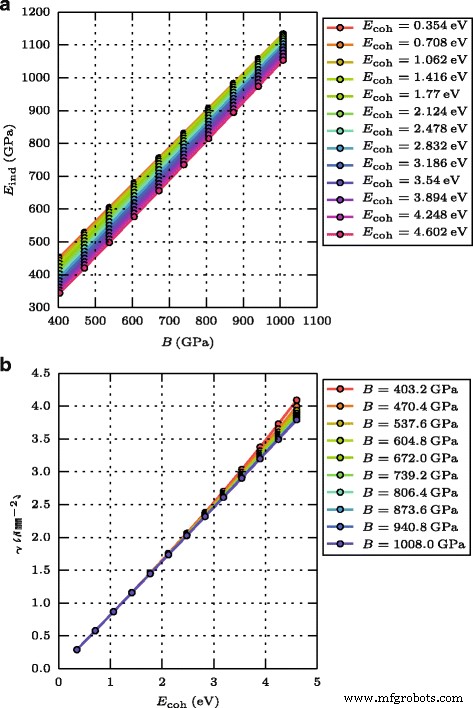
材料参数。 a 的依赖 压痕模量 E 对体积模量的指示 B 和 b 表面能γ 关于内聚能E 哦

(100) 晶面的表面能是通过将块状晶体和具有开放 (100) 表面的晶体的能量差除以开放表面的面积来计算的 [13]。图 1b 表明 γ 大致与 E 成正比 哦;偏差仅在刚度较小且结合牢固的材料中可见。

我们通过切割半径为 R 的球体来构造晶粒 =9a =33 Å 超出 fcc 晶格，包含大约 12,000 个原子。由于它们的构造，它们具有刻面。它们被松弛以平衡它们的表面；轻微的表面松弛，但没有观察到表面的重建。碰撞是通过复制颗粒并以相对速度 v 将它们射向彼此而开始的 .仅考虑中心碰撞，其中两个面向（100）个面正面碰撞，见图 2。

碰撞的初始设置

为了确定弹跳速度，我们执行多个速度的碰撞。此处使用的算法基于简单的二分方案。我们证实，对于这里研究的所有碰撞系统，速度为 250 m/s 的碰撞都在反弹，而在速度消失时，碰撞仍然存在。然后，以最低已知弹跳速度和最高已知粘着速度的算术平均值运行模拟。重复此过程，直到最高粘附速度和最低弹跳速度之间的差异小于其平均值的 10%。 v b 取最高黏附速度和最低弹跳速度的算术平均值；后两个值也用于指示我们在图中计算的误差。模拟使用开源软件LAMMPS[14]进行，代码与我们之前的二氧化硅[7]与水冰粒子碰撞研究[15]中使用的代码基本相同。

结果

图 3 概述了所获得的结果。

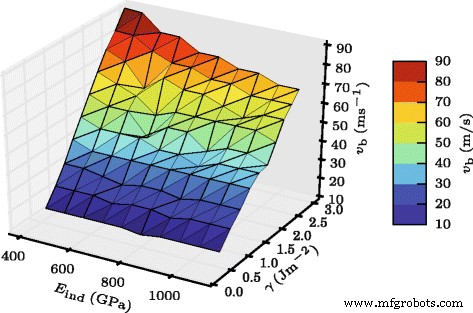
弹跳速度。弹跳速度 v 相关性的三维图 b 关于压痕模量E ind 和表面能γ

因此，JKR 定律的主要特征，方程。 (1)——增加v b 与附着力和弹性刚度的下降-再现，但依赖性比JKR情况下的弱。

图 4 更详细地查看了这些依赖关系。由于我们确定了具有固定 B 的材料的弹跳速度 或 E coh，我们将针对这些固定值分析它们，但以 E 的形式呈现依赖关系 ind 和 γ 为了与 JKR 预测建立联系，方程。 (1).对于恒定内聚能 E 哦，v b 取决于弹性刚度的幂律，

弹跳速度。弹跳速度的相关性 v b 在 a 压痕模量E ind 和 b 表面能γ .线表示幂律拟合。 c 显示幂指数的相关性，a , 方程(4)、关于凝聚力。该线表示引导眼睛的线性拟合

其中 a E =0.28 (0.26, 0.02) coh=3.54 (2.12, 0.35) eV。因此，指数 a JKR 预测的 =0.33 对于高表面能确实几乎可以恢复；然而，随着γ的减少，依赖性变得更软 并且对于弱粘性表面完全消失。注意在表面能消失的情况下，所有的碰撞都必须是弹跳的；这就解释了在这种情况下弹性刚度的消失作用。

图 4c 显示了 v 依赖的幂指数 b (E ind), 等式(4)，从我们的模拟中获得。该图清楚地表明对 E 的依赖性增加 如红色线性拟合线所示，随着内聚能和表面能的增加而增加。

对于固定弹性刚度，B , v 的依赖 b 在 γ 显示了一个更简单的图片，见图4c。幂律拟合，v b ∝γ ^-b , 给出相当一致的 b 值 B =0.67 (0.59, 0.53) =403 (739, 1008) GPa，因此对 B 仅表现出轻微的依赖性 因此 E 工业但是请注意，这些依赖项比 b 的值要软 =0.83 由方程预测。 (1).随着刚度的增加，与 JKR 预测的偏差变得更大。事实上，众所周知，JKR 对于太硬的系统会失败 [16, 17]。对于此类系统，Derjaguin-Muller-Toporov (DMT) 理论 [18] 被认为更适用；然而，似乎没有从该理论中得出对弹跳速度的预测。

总的来说，这里发现的弹跳速度低于 100 m/s。我们强调，对于适合 Cu 的 Morse 势的实际值，我们发现在整个速度范围内都保持不变，并且没有弹跳。这与 Pogorelko 等人最近对铜球（直径 7-22 nm）与铝表面碰撞的模拟一致。 [19, 20] 谁发现速度高达 1000 m/s。我们在模拟中确实发现弹跳的原因是我们使用模型势，其中弹性模量大大增加，表面结合减少，相对于表征真实 Cu 的值。

在弹跳阈值之上，碰撞的特征在于恢复系数，

比较碰撞后的相对速度，v ^′ , 到碰撞前, v ，从而测量碰撞的非弹性。对于粘连碰撞，显然，e =0。 JKR 理论提出了一个规律 [4-6]

我们引入了因子 α 考虑能量耗散[7]。

图 5 显示了 e 速度依赖的两种情况;我们发现这些代表了所研究的整个刚度和附着力值范围。在所有这些情况下，碰撞过程中没有大的能量耗散； α 大约是 0.9。在足够大的表面能下，图 5a，e 很好地遵循 JKR 预测，方程。 (6).在小 γ ，然而，图 5b，可以看到一个较窄的过渡区，其中 e 从 0 切换到几乎 1； JKR 预测，方程 2 没有很好地描述这个过渡区。 (6).

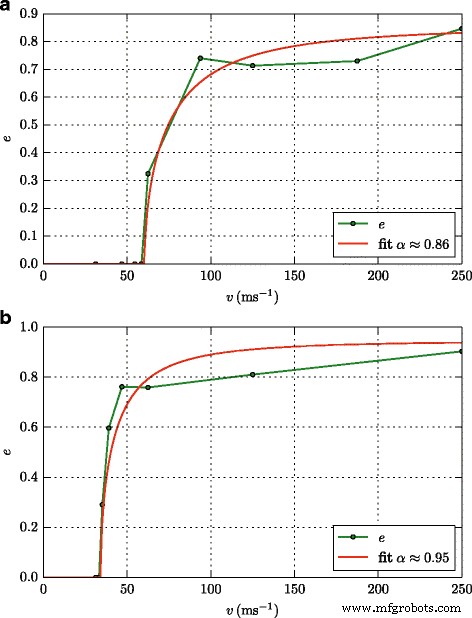
恢复系数。恢复系数的相关性，e ，关于碰撞速度，v , 对于强 (γ =2.32 J/m ² ) (a ) 和弱 (γ =0.89 焦/米 ² ) (b ) 粘合面。两种情况下的体积模量相同，B =940.8。符号表示模拟结果，而曲线是对 JKR 预测的拟合，方程。 (6)、与α =0.86 (a ) 和 0.95 (b )

讨论

在粘附状态下，恢复系数保持在 1 以下，表明碰撞过程中的非弹性能量损失。我们验证了碰撞是纯弹性的，因为碰撞过程中没有产生永久可塑性；软件工具 OVITO [21] 用于检查位错产生。对于更高的速度，v>100 m/s 和柔顺的球体，位错是瞬时形成的，但在碰撞后又消失了。我们注意到，在通过通用 Lennard-Jones 势相互作用的类似尺寸的结晶纳米球碰撞期间，可以检测到大量的位错产生 [22, 23]，而在无定形二氧化硅球体的碰撞中识别出剪切转变区 [7]，两者因此碰撞系统表现出可塑性。在我们的例子中，高弹性模量阻止了塑性变形的建立；非弹性能量损失仅由碰撞球体中的振动激发引起。可以得出结论，弹跳碰撞的存在与碰撞过程中非弹性损失的抑制以及塑性变形的抑制有关。

e 的行为 对于小γ 强调了我们对 v 的上述发现 b 对于弱粘合系统，表现出与 JKR 的较大偏差。我们得出结论，对于弱粘附，弹跳速度以及弹跳后系统的状态仅微弱地依赖于其他系统特性，例如 E ind 和 v .

结论

粘合弹性接触的 JKR 理论的预测已经通过使用模型电位的纳米颗粒的专用 MD 模拟进行了测试。我们发现，当将材料刚度和材料附着力改变一个数量级时，JKR 理论可以很好地再现弹跳速度依赖性的总体趋势。然而，我们发现弱粘附颗粒的系统偏差；在这种情况下，弹跳阈值变得与材料刚度无关，并且恢复系数在 v 以上几乎不表现出速度相关性 b .同样为了更强的附着力，弹跳速度对 γ 的依赖性 系统地小于 JKR 预测的。

这些偏差表明宏观接触理论对纳米粒子碰撞的描述不完整。未来的工作将尝试将这项研究扩展到具有其他取向和更大半径的晶粒以及非晶晶粒。