纳米级应变场对 AlN 折射率的影响

介绍

AlN 基材料是制造深紫外 (DUV) 光电器件的有前途的材料，例如发光二极管 (LED) [1,2,3,4,5]、激光二极管 [6,7,8] 和光电探测器 [ 9, 10] 由于直接带隙可调，可从 3.4 到 6.2 eV [11]。 AlN的折射率直接影响光电器件的性能。对于 LED 而言，AlN 的折射率对光提取效率 (LEE) 有影响，因为全内反射角由 AlN 层与其他区域之间的折射率差异决定，这是影响光提取效率的关键因素的光输出。由于外量子效率 (EQE) 是内量子效率和 LEE 的乘积，因此 AlN 的折射率会影响 LED 的 EQE。此外，折射率在波导结构的设计中起着关键作用，例如分布式布拉格反射器 (DBR) [12,13,14]，其反射率对折射率很敏感。因此，揭示影响AlN折射率的因素具有重要意义。从以往的研究可知，AlN的折射率受温度、压力、带隙等多种因素的影响。 AlN 的折射率随着温度升高 [15] 和压力降低而增加 [16]。对于基于 AlN 的材料，折射率随着带隙的增加而降低 [17]。此外，半导体中的位错对半导体的性质和器件的性能有很大的影响。位错将释放材料中的应力 [18]。它们还会影响光电探测器的暗电流和响应度 [19]，并影响多个量子阱的 IQE [11, 20] 等。然而，很少有研究关注不同的穿透位错密度（TDDs）对AlN折射率的影响，尽管AlN材料中的TDDs很高，通常在10 ⁸ 到 10 ⁹ cm ^{− 2} 来自最近报告的订单 [21,22,23]。研究 TDD 与 AlN 折射率之间的相关性是优化光电器件性能的关键。在本文中，研究了不同 TDD 对 AlN 折射率的依赖性。使用不同的光子波长，例如 633 nm、365 nm 和 280 nm。结果表明，位错导致AlN的折射率降低。研究结果将有助于DUV LED、DBR结构等AlN基光电器件的设计与仿真。

方法

为研究位错与AlN折射率之间的关系，采用金属有机化学气相沉积（MOCVD）在c-蓝宝石衬底上生长AlN模板，然后在不同温度下退火，获得不同位错密度的AlN样品。

当通过 MOCVD 生长 AlN 模板时，三甲基铝和氨被用作前体气体。氢气用作载气。生长期间的压力保持在40 mbar。成核层的生长温度和时间约为 955 °C，持续 150 s，然后升高到 1280 °C 以进行高温 (HT) AlN 生长。经过 15 分钟的高温 AlN 生长后，AlN 中间层在 1050 °C 下生长 160 s。最后，将生长温度提高到 1280 °C，以生长厚的 HT AlN 50 分钟。 AlN薄膜的总厚度约为1.1 μm。

在通过 MOCVD 生长 AlN 层后，AlN 模板分别在 1500 °C、1600 °C、1700 °C 和 1750 °C 下异位退火 1 h。未退火的AlN层标记为样品1，1500 °C至1750 °C退火后的样品标记为样品2至5。 X射线衍射（XRD）用于测量AlN样品中的TDD，以及进行光谱椭偏 (SE) 测量以测量折射率。采用拉曼位移光谱表征AlN模板的应力状态。

结果与讨论

图 1a 和 b 显示了五个 AlN 样品的 (0002) 和 (10-12) 面 XRD 摇摆曲线 (XRC)。可以观察到，从样品 1 到样品 5，(0002) 面 XRC 的半峰全宽 (FWHM) 略有减小，(10-12) 面 XRC 的 FWHM 大大减小。可以根据公式（1）和（2）使用（0002）和（10-12）平面XRC的FWHM计算分量：[24, 25]。

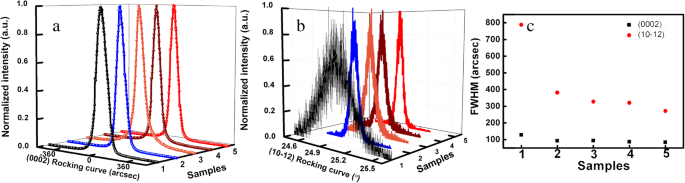
一 五个 AlN 样品的 (0002) 平面 XRC。 b 五个 AlN 样品的 (10-12) 平面 XRC。 c (0002, 10-12)平面XRC的半高宽；红色圆圈表示（10-12）面的半高宽，黑色方块表示（0002）面的半高宽

其中 ρ s 和 ρ e 分别用螺旋分量和边缘分量表示位错的密度。 β 是 XRC 的 FWHM。 |b c |等于 c 轴晶格常数，且 |b 一 |等于 AlN 的 a 轴晶格常数。五个AlN样品的（0002）和（10-12）平面XRC的FWHM如图1c所示，五个AlN样品的计算TDD如表1所示。

五个样品的SE实验数据由CompleteEASE软件（J.A. Woollam Inc.）使用参数半导体模型拟合，可以有效再现直接带隙半导体的光学特性[26]。图 2a 显示了五个样品的部分实验和拟合曲线。五个样本的均方误差 (MSE) 分别为 8.139、8.536、9.175、10.560 和 9.821，证实了良好的拟合结果。附加文件 1 中提供了所有数据和拟合结果。

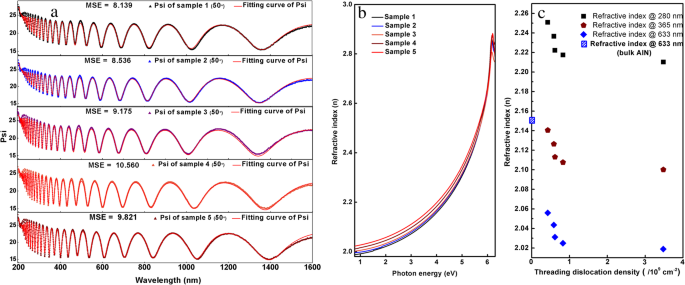
一 SE测量和拟合曲线的部分实验数据。 b 折射率曲线。 c 在 280 nm、365 nm 和 633 nm 处的折射率与不同 TDDs 的关系

五个样品的折射率曲线可以从拟合结果中获得，如图 2b 所示。当光子能量低于 AlN 的带隙（约 6.2 eV）时，所有五个样品的折射率都随着光子能量的增加而增加。然而，当光子能量高于 6.2 eV 时，折射率随着光子能量的增加而降低。这种现象可以用 Kramers-Krőnig 色散关系来描述。随着 AlN 中 TDD 的减少，在 633 nm 处的折射率从 2.019 增加到 2.056，这更接近于块状 AlN（在 633 nm 处为 2.15 [27]）。这意味着AlN中的位错使折射率小于块状AlN晶体的折射率。

在 4.42 eV（280 nm，日盲紫外线）、3.40 eV（365 nm，GaN 的带隙）和 1.96 eV（633 nm）处的折射率和 TDD 之间的关系如图 2c 和表 1 所示可以看出AlN的折射率随着TDDs的增加而降低。随着位错密度从 4.24 × 10 ⁸ 到 3.48 × 10 ⁹ cm ^{− 2} ,AlN在280 nm处的折射率从2.2508下降到2.2102。

为了揭示位错如何改变AlN折射率的机制，研究了位错引起的应变场。折射率与应变场的关系由式(3)[28]表示：

在公式中，p ij 是弹光张量和 S 是应变的存在。光弹性常数矩阵P 纤锌矿AlN的性能如表达式（4）[29, 30]。

考虑了AlN中螺型位错和刃型位错的应变场矩阵。两种位错的圆柱环模型如图3所示，根据模型可以得到单个位错周围的应变场分布[31, 32]。

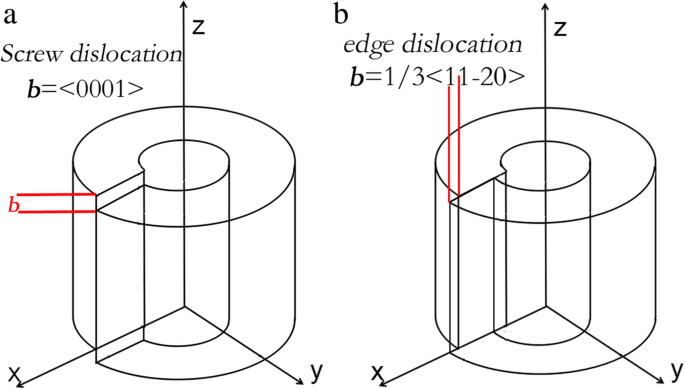
a的圆柱环模型 螺钉错位和b 刃位错

单位螺位错周围的应变场可写为：

单位边缘位错周围的应变场可写为：

其中 b 是单位位错的 Burgers 向量的长度，e 代表位错周围的应变。 G =121 GPa为纤锌矿AlN的剪切模量； λ =117.1 GPa 和 v =0.241 分别是跛脚常数和泊松比 [33, 34]。根据 e 之间的对应关系 ij 和 S k (i ,j =x ,y ,z; k =1,2,3...6) [35]，我们将应变场转化为基体形成如下，以进一步呈现位错引起的折射率变化。

将矩阵(7)和(8)代入式(3)，可得Δn的表达式 由单元螺钉和单元边缘错位引起。

根据计算，单位螺和单位刃位错周围的折射率分布（以633 nm处的折射率为例）如图4所示，表明位错周围的折射率沿径向变化位错核可被视为非均质介质。因此，在 AlN 中传播的光将相应地受到 TDD 的影响。当光穿过这些位错周围的折射场时，就会发生散射和干涉 [36]。结果，AlN的折射率会发生变化，这与非均匀介质的散射矩阵[37]相对应。

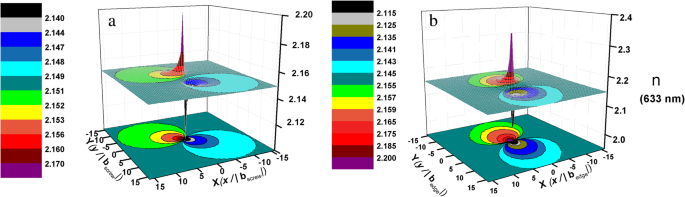
a附近633 nm处的折射率分布 单元螺钉错位和b 单位边缘位错

如“简介”部分所述，应排除其他影响因素，以证明折射率确实受到位错的影响。所有样品均在室温下测量，以消除温度的影响。为了消除AlN材料中应力的影响，采用拉曼光谱来确认AlN中的应力，结果如图5所示。E g 蓝宝石的模峰在 750 cm ^{− 1} 被视为校准。 AlN E 的拉曼位移峰 2(h ) 随着 TDD 的减少而发生蓝移，如表 1 所示。 E 的蓝移 2(h ) 峰值意味着 AlN 承受越来越多的来自蓝宝石衬底的压应力。然而，随着压应力的增加，633 nm处的折射率变得更接近块状AlN的折射率。可以清楚地得到，AlN 的应力受到异质衬底的影响，对折射率的影响很小。支持该结论的其他证据是，当 AlN 受到来自 Si 衬底的拉应力时，AlN 的折射率也小于体 AlN 的折射率 [38]，这与本工作中 AlN 受到压应力的条件相同。这种现象可归因于AlN 的应力受到衬底的影响太小而无法对AlN 的折射率产生显着变化。因此，与其他因素的影响相比，衬底应力对AlN折射率的影响可以忽略不计。

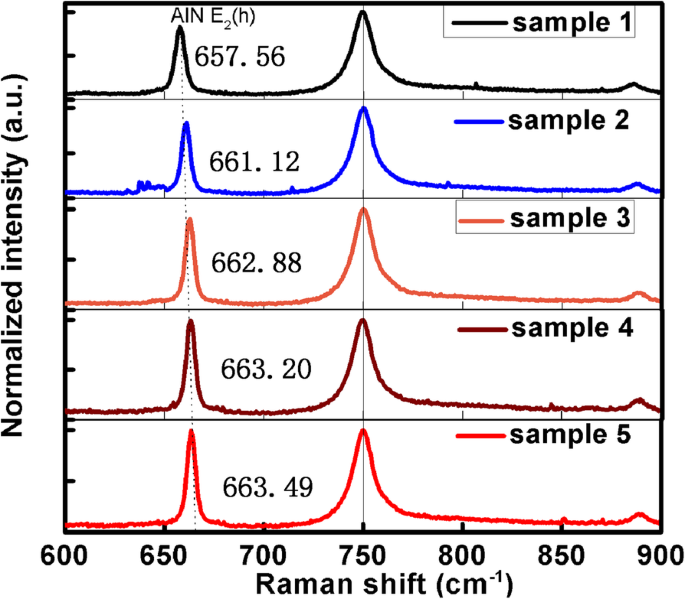
五个样品的拉曼位移光谱

此处还计算了五个样品的带隙。光吸收系数α 从 SE 拟合结果中提取，然后带隙 E g 根据以下公式计算[39]：

(αE ) ² 对比 E 如图 6.x 的截距 -axis 是 E 的值 g .从 x 上拟合曲线的截距 轴，样品1到样品5的带隙从6.1106增加到6.1536 eV如图6所示。折射率与带隙的关系如下图[16]。

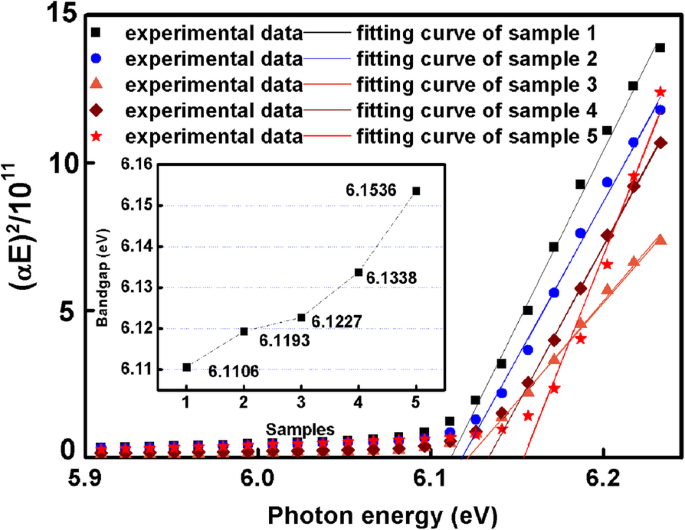
(αE的依赖 ) ² 在 (E )，插图显示了AlN模板的带隙

其中 E 是光子能量和 E g 是 AlN 的带隙。 一 和 b 是常数，对于 AlN，分别等于 13.70 和 7.81。 AlN的折射率应随着E的增加而降低 g 根据公式。然而，在这项工作中，AlN 的折射率随着 E 的增加而增加 g ，这意味着与 TDD 的影响相比，带隙对 AlN 折射率的影响可以忽略不计。因此，TDDs的变化对AlN折射率的变化起着关键作用。

结合以上分析，确定纳米级应变场会影响位错周围的折射率分布，进而影响AlN的折射率。根据实验数据，位错会降低AlN的折射率。

结论

总之，TDDs 对 AlN 折射率的影响在实验和理论上进行了研究。排除温度、应力和带隙的影响，可以得出结论，AlN 的折射率随着 TDD 的增加而降低。进一步的研究表明，位错周围的纳米级应变场导致位错周围的折射率发生显着变化。一旦光通过位错传播，就会发生散射和干涉，从而改变 AlN 的折射率。本工作的研究结果将有利于优化基于AlN的DUV光电器件。

数据和材料的可用性

所有数据都可以根据适当的要求提供。

缩写

DBR：

分布式布拉格反射器

DUV：

深紫外线

EQE：

外量子效率

FWHM：

半高全宽

LED：

发光二极管

LEE：

光提取效率

MOCVD：

金属有机化学气相沉积

MSE：

均方误差

SE：

光谱椭偏仪

TDD：

螺纹位错密度

XRC：

XRD摇摆曲线

XRD：

X射线衍射