通过二维纳米多孔膜的单文件水通量

介绍

在涉及合成膜 [1, 2] 或天然膜 [3, 4] 的亚纳米纳米孔中观察到单列水传输。这些亚纳米孔中的单列水形成通过形成脱水的自由能垒有效地阻碍了离子易位 [5]。在发现碳纳米管 (CNT) 膜中的快速水通量率和高脱盐率 [2, 6] 后，研究了许多其他因素，例如边缘功能化、电荷分配和表面改性，以了解传输机制并提高膜的效率 [7,8,9,10]。此外，通过将氧化石墨烯的层间距调整到亚纳米级，氧化石墨烯膜已成功用于离子筛分[11]。

由石墨烯引发的二维 (2D) 膜的发现 [12]，在过滤和海水淡化膜领域引起了极大的关注 [13]。由于其一个原子厚的孔隙宽度，理论上可以将摩擦压力损失降至最低，并可以获得优异的水通量[14]。纳米多孔单层石墨烯已通过使用氧等离子体蚀刻工艺成功制造，可以控制孔径 [15, 16]。它已成功用于海水淡化膜，具有近 100% 的脱盐率和高达 10 ⁶ 的高水通量 克/米 ² s [16]。执行分子动力学 (MD) 模拟也证明了高脱盐性能 [17]。此外，纳米多孔石墨烯膜在气体分离[18, 19]和离子分离[15, 20]方面表现出高效的分子筛分。

在成功合成石墨炔 [21, 22] 后，其他二维石墨烯衍生物如石墨炔、石墨酮和石墨烷作为一类新型二维材料受到了极大关注 [23, 24]。此外，还引入了使用孔功能化或化学掺杂的表面改性来扩展 2D 膜的功能。氮 [25] 或镍 [26] 掺杂表现出优异的催化活性。冠醚已嵌入石墨烯纳米孔中，用于机械敏感离子易位活动 [27] 或选择性离子易位 [20, 28]。使用吡啶氮、氟或羟基的石墨烯纳米孔功能化在 MD 模拟中表现出增强的脱盐效率 [29,30,31]。石墨炔 3 和石墨炔 4 具有天然的高孔隙率，也被证明具有较高的滤水率和脱盐率，是海水淡化膜的潜在候选材料 [32]。

此外，近年来开发并广泛研究了先进的二维材料，如硅烯 [33]、锗烯 [34, 35]、六方氮化硼 (hBN) [36, 37] 和金属有机骨架 (MOF) [38] .二维材料的发展已经扩展到结构不对称的 Janus 二维材料，例如 MoSSe [39, 40] 和 In2SSe [41]。使用 MD 模拟，诸如 MOF [42] 和 MoS2 [43] 等新型 2D 材料已表现出有效的脱盐性能。在实验中，已经合成了薄至 3 nm 的 MOF 膜并进行了纳滤测试 [44]。还合成了薄至 7 nm 的 MoS2，并对其脱盐效率进行了测试 [45]。它们都表现出高水过滤率和染料/盐去除率。 MD 研究发现 2D hBN 表现出更高的水渗透率 [46] 优于石墨烯膜。

预测各种二维膜作为水过滤膜的效率需要了解表面化学性质对水传输速率的影响。表面亲水性在界面处的水动力学中起着至关重要的作用 [47]。在本研究中，通过调节膜-水相互作用强度来调节表面亲水性，并通过使用 MD 模拟研究其对水流速的影响。为了表示单层 2D 膜，选择六边形石墨烯结构作为 2D 模型结构。将通过 2D 膜的单列水流与通过三维 (3D) 膜的水流进行比较，其中水易位长度对应于多个原子尺寸。为了表示3D膜，具有石墨烯板的CNT结构被用作3D模型结构。

方法

从石墨烯和碳纳米管的几何结构中获得2D膜和3D膜结构，如图1所示。2D膜中的纳米孔是通过从孔中心（指定为R2）去除圆形区域内的原子而产生的。由此产生的孔隙区域呈六边形，其中最远原子之间的距离约为 7.52 Å。通过在相距 2.06 nm 的两个石墨烯板之间插入 (6,6) CNT 结构获得 3D 膜结构。 3D 和 2D 膜的孔面积之间存在细微差异。生成了由 CNT 边缘和石墨烯板组成的额外 2D 膜结构，以消除孔径差异的影响。该配置被指定为 R1。 R1 构型的孔半径对应于 (6,6) CNT 的半径，为 8.13 Å。

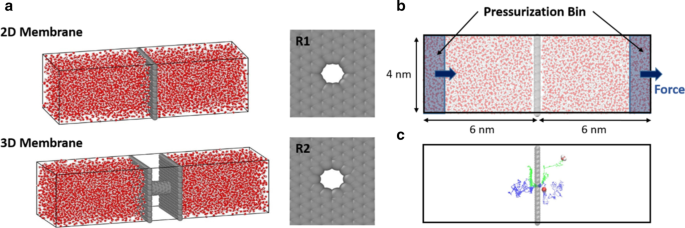
一 具有 2D 和 3D 膜结构的模拟单元。 R1 显示了 3D 膜的孔入口配置。对于二维膜结构，使用了 R1 和 R2 入口配置。黑框线代表模拟单元的周期性边界。 b 在压力驱动的水流模拟中对水分子施加力。 c 水分子穿过二维膜的代表性轨迹

膜的平面尺寸为 4.12 × 4.08 nm。对于 2D 膜模拟，初始模拟框大小为 4.12 × 4.08 × 12 nm，对于 3D 膜模拟为 4.12 × 4.08 × 14.06 nm。在 x 中应用周期性边界条件 , y , 和 z 方向沿着模拟框，如图 1 所示。膜被放置为垂直于 z - 模拟框中心的方向 (z =6 纳米）。 SPC/E 水模型 [48] 用于填充模拟框，因为该模型与实验传输特性（如扩散率 [48, 49] 和粘度 [50, 51]）非常吻合。水分子总数为6474。水分子与膜之间的非键相互作用由Lennard Jones (LJ)相互作用计算，

其中\(\varepsilon\) 是势阱的深度，\(\sigma\) 是电位为零的原子之间的距离，r 是原子之间的距离。在这些模拟中，\(\sigma\) 固定在 0.33 nm，这是碳和水距离参数的算术平均值。水膜相互作用强度 \(\varepsilon ,\) 从 0.026 变为 0.415 kcal/mol 以调整亲水性。本研究中使用的相互作用强度对应于 0.25 \({\varepsilon }_{0}\), 0.5 \({\varepsilon }_{0}\), \({\varepsilon }_{0}\) , 2 \({\varepsilon }_{0}\) 和 4 \({\varepsilon }_{0}\)，其中 \({\varepsilon }_{0}\) 是碳之间的 LJ 相互作用强度[52] 和氧气 [48]。

所有模拟均使用 GROMACS 软件 [53] 进行。使用 Leapfrog 算法进行时间积分，时间步长为 1 fs。使用 Nosè-Hoover 恒温器 [54] 将温度保持在 300 K，时间常数为 0.1 ps。截止方案用于计算 LJ 相互作用，截止距离为 12 Å。长程静电相互作用是通过使用粒子网格 Ewald (PME) 方法计算的，实空间截止值为 12 Å，倒易空间网格为 1.2 Å。在初始平衡模拟期间，通过应用 Parrinello-Rahman 恒压器将垂直于膜的水压调整为 1 bar [55]。 NPT 平衡 1 ns 后，系统使用 NVT 系综进一步平衡 1 ns。在总共 2 ns 的平衡之后，通过对驻留在加压仓中的水分子施加力来模拟压力驱动的流动 [14, 56]。 1 nm 长的加压仓位于模拟箱的侧面，如图 1b 所示。作用在水分子上的外力的计算公式为\(f=\Delta P/NA\)，其中\(\Delta P\) 是所需的跨膜压差，N 是加压仓中的水分子数，A是膜面积。从先前的文献中可知，该方法能够在模拟过程中很好地保持所需的压降 [14]。压力驱动的流动模拟了 10 纳秒，并在 1 纳秒初始化后收集了 9 纳秒的数据。在模拟过程中，膜被视为刚性材料。

进行模拟后，分析了水的结构和输运特性。孔轴方向的扩散系数由爱因斯坦关系式计算得到，公式为

通过关系式[57]，通过积分作用在水分子上的力来计算平均力的潜力（PMF），

其中 \({z}_{0}\) 是大量水的位置。 \({z}_{0}\) =3 nm 在本研究中。在z中ΔPMF和扩散系数分布的计算 -方向，沿纳米孔轴使用半径为 3.8 Å 的圆柱形容器。

结果与讨论

水通量

在跨膜施加压降期间，计算通过膜移位的水分子的数量，如图 2a、b 所示。图 2a、b 分别表示通过 2D (R1) 和 3D (R1) 膜的水易位数量。从水易位与时间的斜率，测量平均水通量。在图 2c 中，测量的水通量与 2D 和 3D 膜的相互作用强度一起绘制。随着相互作用强度的增加，水通量急剧增加到最大水通量，然后在所有膜中单调减少。在二维膜中，R1 的水通量略高于 R2。差异是由于R1的水可及区域稍大。

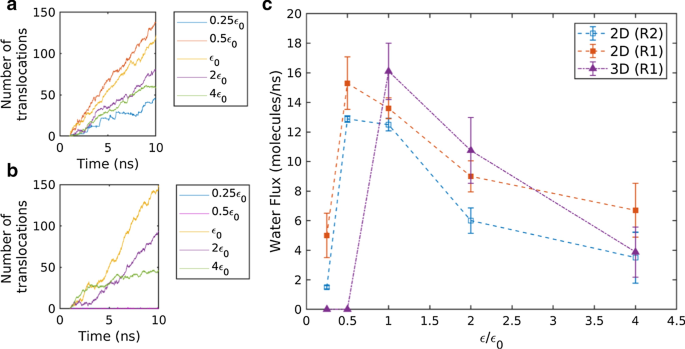
一 二维膜中随时间易位的水分子数，b 3D 膜中随时间易位的水分子数量，c 计算出的水通量（每 ns 易位水分子数）随水膜相互作用强度的变化

在低相互作用强度下最小水通量到最大水通量的转变归因于孔隙去湿-润湿转变。在具有亚纳米直径的纳米孔中，水分子排列为单列链 [1, 58]，如图 3e、f 所示。形成单列的水分子的氢键数量减少到大约一个半[59]。在单列的形成过程中，失去的氢键能被膜-水相互作用能部分补偿[1]。在描述疏水孔的低膜-水相互作用强度下，膜-水相互作用不能提供足够的补偿来形成单列链。这种去湿行为在压力驱动和平衡模拟中都得到了证实，通过绘制密度分布图和测量占据数（详见“水密度”部分和“纳米孔中的水占据”部分）。

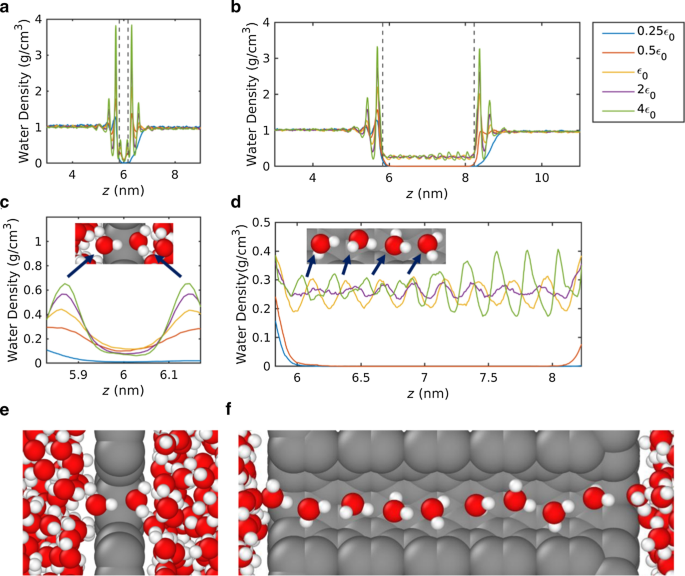
一 –d 水密度分布和e –f 在 MD 期间可视化单列水形成。 a沿纳米孔轴向的水密度 2D 膜和 b 3D 膜。在具有水可及孔隙半径的圆柱形箱中测量密度。 c 孔隙区域内的详细密度剖面 2D 膜和 d 3D 膜。 e 中的单文件配置 2D 纳米孔和 f 3D纳米孔

2D 和 3D 膜表现出阈值相互作用强度的差异。 3D 膜的阈值相互作用强度高于 2D 膜。在亚纳米孔隙内部，部分链或单个水分子在能量上是不利的。因此，孔内完整的链形成是亚纳米孔润湿的先决条件。相对较短的链长度和位置紧密的本体水浴能够以相对较低的相互作用强度润湿二维膜。由于阈值相互作用强度的这种差异，在低相互作用强度 (0.25 \({\varepsilon }_{0}\) 和 0.5 \({\varepsilon }) 下，2D 膜的水通量高于 3D 膜的水通量_{0}\)).

在阈值相互作用强度润湿纳米孔时，达到最大水通量。然后，水通量随着相互作用强度的增加而降低。据报道，疏水表面促进边界滑移，并随后增强水通量 [60,61,62]。当应用滑动边界条件时，连续流体动力学也控制着增强的水通量。由于孔轴向和径向的亚纳米尺寸，相同机制在单列通量和二维膜上的有效性尚不清楚。为了解释水通量随着亲水性的增加而降低，研究了水动力学和能量学（参见“水扩散率”和“平均力的潜力”部分）。请注意，与 2D 膜相比，3D 膜的水通量降低更为显着。在中等相互作用强度 (\({\varepsilon }_{0}, 2{\varepsilon }_{0}\)) 下，3D 膜优于 2D 膜，而在高相互作用强度 (4 \( {\varepsilon }_{0})\).

水密度

沿孔隙轴向的水密度分布如图 3a-d 所示。使用具有孔隙半径的圆柱箱测量水密度，以获取开孔区域的密度分布。图 3a 和 b 分别表示 2D 和 3D 膜的水密度分布，其中孔区域由虚线表示。孔隙区域的宽度定义为膜原子的范德华直径。由于膜原子的中心位于z =6 nm，孔隙区域定义为 z =5.83–6.17 nm（对于 2D 膜）和 z 对于 3D 膜，=5.83–8.23 nm。在图 3c、d 中，显示了孔隙区域内的水密度。

在孔隙入口的近端区域，可以清楚地观察到明显的密度峰谷，代表分层的水结构。之前的 MD [63] 和实验研究 [64] 已经报道了实体壁附近的分层水结构。由于孔隙半径小于范德华相互作用作用的距离（~ 1.2 nm），尽管孔隙是开放的，层状水结构并没有消失。从密度振荡可以看出，密度峰的大小随着相互作用强度的增加而增加。

孔隙区域内的密度峰值表明水分子形成单列的有利位置。在二维纳米孔中，两个密度峰表明两个水分子形成一个稳定的单列。在 3D 纳米孔中，观察到 8 到 9 个密度峰，表明构建了更长的水链（图 3e、f）。孔隙区域内的零水密度表明没有水分子透过膜。在二维纳米孔中，水密度接近于零，相互作用强度为 0.25 \({\varepsilon }_{0}\);因此，2D 纳米孔的水通量是标称的，相互作用强度为 0.25 \({\varepsilon }_{0}\)。在 3D 纳米孔中，当相互作用强度为 0.25 \({\varepsilon }_{0}\) 和 0.5 \({\varepsilon }_{0}\) 时，水密度为零，这意味着 3D 测量的水通量为零具有这些相互作用强度的纳米孔。

纳米孔中的水位

还通过在没有外部压力差的情况下运行平衡模拟来研究平衡水动力学。通过计算每个时间段内孔隙区域内水分子的瞬时量来测量纳米孔的水占据数。图 4a-l 显示了 2D 和 3D 膜的各种相互作用强度随时间的占用数。从图 4 中可以看出，水占据证明了纳米孔的水空填充两态转变。众所周知，这是单列水的特征，因为部分填充（破碎的单列）状态在能量上是不利的 [1]。在 0.25 \({\epsilon }_{0}\) 的低相互作用强度下，2D 和 3D 膜的空状态（0-1 水占有率）更多。在这种强度下，2D 膜的平均占用数为 0.37，3D 膜的平均占用数为 0.05。在 0.5 \({\epsilon }_{0}\) 的相互作用强度下，2D 膜的填充状态（1-2 水占有率）更多，而 3D 膜仍然填充空状态。在这种强度下，2D 膜的平均水占有数为 1.1，3D 膜的平均水占有数为 0.3。在\({\epsilon }_{0}\) 的相互作用强度下，3D 膜的占用数为 8-10。这表明 3D 膜处于填充状态，相互作用强度为 \({\epsilon }_{0}\).

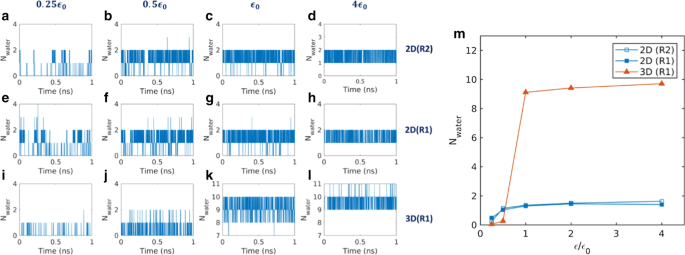
a 纳米孔内的水占有数 –h 2D 和 i –l 3D 膜。 a 的膜-水相互作用强度为 0.25 \({\epsilon }_{0}\) , e , 和 i , 0.5 \({\epsilon }_{0}\) 对于 b , f , 和 j , \({\epsilon }_{0}\) 对于 c , g , 和 k , 和 4 \({\epsilon }_{0}\) 对于 d , h , 和 l .平均职业数随交互强度(m )

平均水占有数随相互作用强度的变化如图 4m 所示。还观察到空填充两态过渡行为与相互作用强度。随着占用数从标称数跃升到高数，然后随着相互作用强度的增加而略微增加，3D 膜的急剧转变可以清楚地观察到。在二维膜中观察到类似的过渡行为；然而，二维膜由于短的单列链长度和紧密的本体水浴而表现出适度的转变，这控制了相对有利的过渡状态。

空填充（去湿-润湿）状态的过渡行为支持低相互作用强度下的水通量变化。低于阈值相互作用强度，由于施加的压降，水通量为零或标称值。在 0.5 \({\epsilon }_{0}\) 的相互作用强度下，2D 膜的水通量比 3D 膜高得多。在这种相互作用强度下，2D 膜处于润湿状态，而 3D 膜处于去润湿状态。因此，可以得出结论，在低相互作用强度下，水去湿是造成水通量变化的原因。遗憾的是，水占有率不能解释水通量随着相互作用强度的增加而减少。

水扩散率

为了进一步研究水动力学，通过平衡模拟计算了水扩散系数。在密度剖面中，观察到近端孔隙区域的大振荡，这表明水层结构。密度振荡的幅度随着相互作用强度的增加而增加。为了考虑这种结构效应，计算了孔隙附近和入口区域的水扩散系数，并将其绘制在图 5a-e 中。图 5a 展示了水分子在各个区域的扩散系数，包括邻近区域和入口区域。很明显，扩散系数随着相互作用强度的增加而降低。因此，可以得出结论，随着相互作用强度的增加超过阈值相互作用强度，水扩散率的降低导致了水通量的降低。

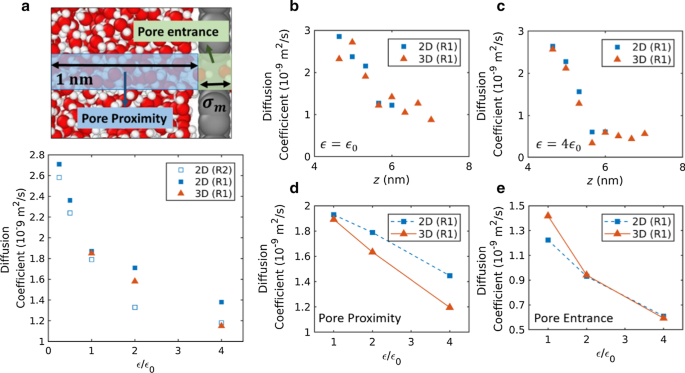
孔隙邻近和孔隙入口区域的水扩散系数。孔隙邻近区域定义为具有孔隙半径和 1 nm 长度的圆柱形区域。孔隙入口区域定义为具有孔隙半径和范德华直径的圆柱形区域。 一 扩散系数随相互作用强度的变化。扩散系数是按区域测量的，包括孔隙入口和邻近区域。 b , c b相互作用强度下沿孔隙轴向的扩散系数分布 \({\epsilon }_{0}\) 和 c 4 \({\epsilon }_{0}\)。 d , e d中扩散系数随相互作用强度的变化 孔隙邻近区域和e 孔隙入口区

显示了中等相互作用强度 (\({\epsilon }_{0}\)) 和高相互作用强度 (4 \({\epsilon }_{0}\)) 的孔隙轴向扩散系数分布分别在图 5b、c 中。在图 5b-e 中，比较了 2D 和 3D 纳米孔的相同孔配置 (R1)，以消除由孔配置差异引起的任何影响。观察到扩散系数从体扩散系数逐渐降低（~ 2.7 × 10 ^–9 m ² /s [49]) 当他们接近孔隙入口时。扩散系数的降低可能是孔隙限制效应和水分层效应共同作用的结果。膜亲水性可能通过两种不同的机制降低扩散系数，即在孔附近诱导高度分层结构和增加孔入口区域的摩擦力。在孔隙邻近区域和入口区域的单独扩散系数计算中（见图 5d、e），扩散系数随着两个区域相互作用强度的增加而降低。

3D 膜的扩散系数略高于或与孔入口区域的 2D 膜相当。相比之下，3D 膜的扩散系数在孔附近小于 2D 膜，并且在高相互作用强度 (4 \({\epsilon }_{0}\)) 下差异显着。在压力驱动的流动模拟中，与 2D 膜相比，通过 3D 膜的水通量随着相互作用强度的降低速度更显着。这导致 3D 膜在中等相互作用强度 (\({\epsilon }_{0},\) 2 \({\epsilon }_{0}\)) 下具有相当或更高的水通量，以及更高的水通量具有高相互作用强度 (4 \({\epsilon }_{0}\)) 的二维膜。在高相互作用强度下，孔隙附近的扩散似乎是这种反向水通量的主要原因。

平均力的潜力

为了进一步研究取决于相互作用强度的膜的优越性，比较了 2D 和 3D PMF 剖面的中等相互作用强度 (\({\epsilon }_{0})\) 和高相互作用强度 (4 \ ({\epsilon }_{0}\))。图 6 中比较了 2D 和 3D 纳米孔的 PMF 曲线。PMF 曲线显示了局部最大值，代表水分子为了通过膜传输而应克服的自由能垒。从 PMF 剖面中，在孔隙入口区域 (z =6 nm) 和孔隙邻近区域 (z \(\大约\) 5.5 纳米)。在\({\epsilon }_{0}\) 的相互作用强度下，邻近能垒在2D 和3D 之间没有表现出显着差异。在 4 \({\epsilon }_{0}\) 的高相互作用强度下，附近的能垒都增加了，但与 2D 膜相比，3D 膜具有更高的幅度。这证实了孔隙邻近是高相互作用强度下反向水通量的主要因素。

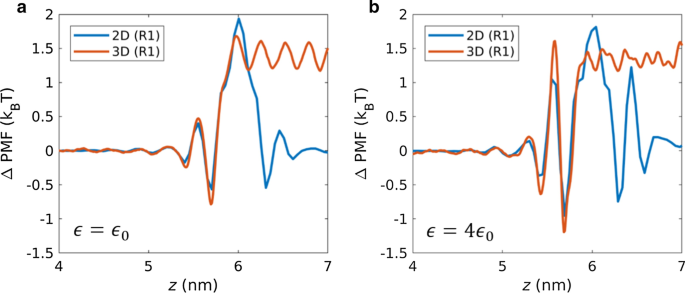
a a 沿孔隙轴向的 PMF 分布 中等交互强度 (\({\epsilon }_{0})\) 和 b 高相互作用强度 (\(4{\epsilon }_{0})\)

随着相互作用强度 (\({\epsilon }_{0}\) → \(4{\epsilon }_{0}\)) 的增加，二维膜的孔入口能垒从 1.94 变为 1.82，1.68对于 3D 膜，为 1.45。随着膜-水相互作用能的增加，入口能垒略有下降。另一方面，随着相互作用强度的增加（\({\epsilon }_{0}\) → \(4{\epsilon }_{0}\)），二维的邻近能垒从 0.4 变为 1.05膜，3D 膜为 0.47 到 1.61。从能量的角度来看，水通量随着相互作用强度的增加而减少，主要是由于近端孔隙区域的能垒增加。与 2D 膜相比，这也与 3D 膜的水通量降低更多有关。当膜 - 水相互作用中等（\（{\epsilon }_{0}\））时，2D 膜的总能垒 (2.34 kBT) 略高于 3D (2.15 kBT) 膜。由于 3D 膜的邻近能垒显着增加，在高相互作用强度（4 \({\epsilon }_{ 0})\)因此，ΔPMF 定量地支持了 2D 膜在高相互作用强度 (4 \({\epsilon }_{0})\) 和 3D 膜在中等相互作用强度 (\({\epsilon }_{0}) \).

对于通过较大孔径的非单列水流，无论相互作用强度如何，都假定 2D 膜优于 3D 膜。从以前的文献[65]中观察到具有较大孔径的CNT膜的润湿-去湿行为与相互作用强度。阈值相互作用强度随着孔径的增加而降低 [65]。由于位置紧密的水库和较短的孔隙长度，与 3D 膜相比，2D 膜将表现出较低的阈值相互作用强度，这与单列流的结果一致。因此，当相互作用强度低时，与通过 3D 膜的水通量相比，2D 膜可能通过更大的孔径显示出更高的水通量。对于高于阈值的相互作用强度，与单列水流相比，通过 2D 膜的水通量可能仍高于 3D 膜的水通量。孔隙附近的 PMF 能垒不会对水流产生太大影响，膜壁与水分子之间的摩擦将成为影响水通量的主要因素。先前的文献报道，对于非单列流，通过 CNT 膜的水通量随着 CNT 长度的减少而增加 [66, 67]。此外，对于非单列流，观察到通过石墨烯膜的水通量高于通过碳纳米管膜的水通量 [14]。

结论

In the present study, the effect of the membrane–water interaction strength on the single-file water flux was investigated. Due to the recent advances in two-dimensional membranes, hexagonal 2D membrane structures were considered and compared with the 3D tube type structure. The main observations are as follows:(1) water flux is zero or nominal below the threshold interaction strength, (2) the threshold interaction strength is lower for 2D membranes compared with 3D membranes, (3) water flux decreases with increase in interaction strength when the interaction strength is larger than the threshold interaction strength, and (4) the decrease in water flux was more significant for 3D membranes compared with 2D membranes.

The zero or nominal flux at a low interaction strength was due to the dewetting behavior, which was supported by the small occupation number and water density inside the pore. Above the threshold interaction strength wetting the pore, the water flux decreases with increase in interaction strength. The increase in the interaction strength resulted in an increased PMF energy barrier and decreased diffusion coefficients at the pore proximity, consequently reducing the water flux. In addition, the water structure and dynamics in the pore proximity were more affected by the interaction strength in the 3D membrane compared with that of the 2D membrane. It resulted in the higher reduction of water flux for 3D membranes, compared with the 2D membranes.

Due to the complicated single-file flux dependency on the interaction strength and membrane dimensions, the superiority of 2D membranes over 3D membranes appears to depend on the interaction strength. For a moderate interaction strength (l \({\epsilon }_{0}\),\({2\epsilon }_{0})\), the 3D membrane shows a slightly higher water flux compared with the 2D membranes. For a low (0.5\({\epsilon }_{0}\)) and high interaction strength (4\({\epsilon }_{0}\)), the 2D membrane shows a higher water flux than the 3D membranes. To conclude, the superiority of 2D membranes over 3D membranes depends on the membrane hydrophilicity due to the wetting–dewetting transition and diffusion dynamics in pore proximity. The present findings will be useful in the design and manipulation of 2D membranes to retain a high filtration flux.

数据和材料的可用性

The datasets supporting the conclusions of this article are included within the article, and further information about the data is available from the corresponding author on reasonable request.

缩写

二维：

二维

3D：

Three dimensional

CNT：

碳纳米管

MD：

分子动力学

hBN:

六方氮化硼

MOF:

Metal organic framework

LJ:

Lennard–Jones

PMF:

Potential of mean force