具有行进表面波的石墨烯层上粒子的速度锁定效应

介绍

最近，在微/纳米尺度上检测到一系列表面波/声子诱导的快速传输和扩散现象。首先，已经广泛研究了沿碳纳米管 [1,2,3,4,5] 或石墨烯带 [6,7,8,9,10] 的热泳现象。通过沿碳纳米管 (CNT) 表面施加轴向热梯度，热波动被证实能够使水连续流过碳纳米管 [11,12,13]。进行非平衡分子动力学模拟以探索利用大石墨烯基板上的热梯度来控制小石墨烯纳米薄片 [6] 运动的可行性。此外，通过分子动力学模拟研究了石墨烯和六方氮化硼 (h-BN) 表面上的热驱动水滴传输 [8, 9]。这些现象被认为与声子的某些模式相关 [14,15,16,17,18,19]。例如，Schoen 等人。将碳纳米管内的热泳运动归因于管的呼吸模式 [1, 20]。帕尼松等人。 [21] 指出石墨烯上的弯曲行波/声子可以将它们的动量传递给吸附物并引起传输。与嗜热现象类似，Angelos 等人。表明石墨烯上温度诱导的传播涟漪可以导致水纳米液滴的快速扩散，比液态水中水分子的自扩散快 2-3 个数量级 [22, 23]。

除了热波动，研究证实振动还可以在碳纳米管 (CNT) 内外传输粒子和液滴 [24,25,26,27]。例如，当线性极化横向声波将线性动量传递给纳米液滴时，纳米液滴以接近 30 nm/ns 的速度沿纳米管传输 [24, 28]。郭等人。证明了振动悬臂内的水分子由离心力驱动，并且可以通过分子动力学模拟从 CNT 的固定端到自由端进行连续流动 [26, 29]。通过使用振动电荷和具有不对称表面能的复合单壁碳纳米管，设计了水分子通过单壁碳纳米管 (SWCNT) 的新型纳米级单向传输 [30]。周等人。 [31] 研究了基于由机械振动驱动的单壁碳纳米管的纳米级水泵中的电流反转，并确认水流敏感地取决于机械振动的频率。 Chang 和 Guo [32] 在碳纳米管中发现了多米诺骨牌，它可以以高达 1km/s 的大速度射出内部分子。在单壁碳纳米管中也证明了可逆的多米诺过程[33]。

由于在纳米尺度上检测到由热波动和振动引起的各种快速扩散和传输现象，证实了表面的上下运动可以增强扩散和传输。波与粒子运动之间的联系尚不清楚，无法统一。一个主要的解释是表面的动量可以传递给表面外的粒子或液滴 [22, 24]。但这种解释无法弄清楚振幅、频率和粒子与表面相互作用之间的关系。此外，Angelos 等人。指出明确偏好石墨烯曲率的一个标志对于石墨烯表面上吸附物的快速扩散是必要的[22]，这表明波浪形表面形态引起的相互作用势与快速扩散密切相关。因此，探索波状表面与外部粒子之间的相互作用对于理解纳米尺度的快速传输和扩散机制至关重要。

在本文中，通过基于 Lennard-Jones (L-J) 对势描述的 vdW 相互作用研究波浪状石墨烯表面外的粒子，MD 模拟证明了波浪状运动与粒子速度之间的相干关系。在一定的先决条件下，即速度锁定效应，确定粒子落在波浪表面上的整体速度与行波保持一致。然后，基于以曲率函数表示的粒子和波面之间的相互作用势建立势水坑理论[34,35,36]。根据该理论，提出了锁速效应的两个前提条件，势水坑理论预测的轨迹和速度与MD模拟结果吻合较好。此外，还分析了波长和幅度以及 vdW 相互作用参数的影响，这表明与检测到的石墨烯表面液滴冲浪现象的调节非常吻合 [22]。波驱动速度锁定效应的机制揭示了粒子速度与波面之间的一种新的相干关系。

方法

MD 模拟在软件包大规模原子/分子大规模并行模拟器 (LAMMPS) 中实现。假设波浪形表面是石墨烯层，其原子序数密度为\(\rho =3.85 \times 10^{19} \,{\text{m}}^{ - 2}\)。石墨烯片最初是平的，带有 z =0 Å，沿 x 的长度为 6344 Å 方向，导致晶胞大小为 6000 个原子。沿y轴 使用周期边界条件，周期长度为 12.2 Å。这里，考虑质量为 \(m =0.83 \times 10^{ - 25} \,{\text{kg}}\) 的球形粒子，以简化模型并重点关注波浪形表面。一开始，粒子被放置在 z =7 Å 和 x =200 埃。它在 z 中的初始速度为 - 50 m/s -direction 和 x 中大约 2000 米/秒 -方向。通过在 z 中设置初始速度的开始时间 -方向，可以控制粒子落在波浪面上的初始位置。

采用反应性经验键序 (REBO) 势来模拟石墨烯原子 [37]。同时，选择Lennard-Jones势来模拟粒子\(P\)和石墨烯中每个碳原子之间的相互作用，

其中 \(\varepsilon =5.92 \times 10^{ - 21} \,{\text{J}}\) 和 \(\sigma =4 \times 10^{ - 10} \,{\text{m}} \)。粒子\(P\)与曲面的平衡高度为\(h =4.2 \times 10^{ - 10} \,{\text{m}}\)，由法向力的条件决定零和仿真结果，详见附加文件1：1。

行波函数为正弦形式，

其中振幅为\(A =1 \times 10^{ - 9} \,{\text{m}}\)，波长为\(\lambda =21.75 \times 10^{ - 9} \, {\text{m}}\) 除非另有说明。角频率取为 \(\omega ={{2\pi } \mathord{\left/ {\vphantom {{2\pi } {10^{ - 12} }}} \right. \kern-\nulldelimiterspace } {10^{ - 12} }}\) 对应于 10 ps 的周期；因此，波速为 \(v_{{{\text{wave}}}} =2175\,{\text{m}}/{\text{s}} =\lambda \omega /2\pi\) .为了触发行波，石墨烯的左 10 Å（即 y \(\in\) [− 10, 0] Å) 在 z 中摆动 -具有上述幅度和频率的方向。此外，带有 x 的碳原子> 6010 Å 被夹住以保持石墨烯片稳定。特别是，如果要模拟平坦的石墨烯片，未夹紧的石墨烯原子也将沿 z 束缚在它们的初始位置 -axis 具有 0.0938 eV//Å2 的弱弹簧常数（除了 A 设置为 0）。

5 K 的初始温度指定给未固定的碳原子。设置该温度是为了消除由石墨烯弯曲和拉伸模式之间的谐波耦合引起的热激活纹波，并专注于机械激发引起的行波效应 [22]。然后该结构以 1 fs 的时间步长在微规范集成 (NVE) 中演化。我们监测了这种演变，发现在整个模拟过程中温度几乎没有变化。

结果与讨论

颗粒在波浪形石墨烯表面和平坦石墨烯表面上的轨迹如图 1 所示，时间间隔为波浪形表面的周期。发现粒子相对于波峰或波谷的相对位置没有变化，这意味着粒子被锁定在波浪面上，其速度等于波速。相比之下，粒子在平面上的整体运动明显慢于初始位置相同的波浪面上。由于摩擦，粒子在平坦表面上的速度迅速减小，而摩擦似乎不适用于波浪状石墨烯表面上的粒子。更多具有不同模拟温度和波函数参数的MD模拟案例显示在附加文件1中： 1. 模拟Xe原子和分子C60在波浪和平坦表面上运动以确认该现象的普遍性并显示在附加文件中1：2。

波浪状和平坦石墨烯表面上粒子的运动轨迹

为了理解纳米级速度锁定效应的机制，通过考虑波状表面S之间的相互作用建立模型 和一个外部粒子 P ，如图 2a、b 所示。假设波浪面的波长和振幅为\(\lambda\)和A ，分别是 P 之间最近的高度 和 S 是 h , S 的数密度 是 \({\rho }_{s}\)。在MD模拟中，粒子P之间的相互作用 和波状表面作为vdW相互作用，用L-J势描述，

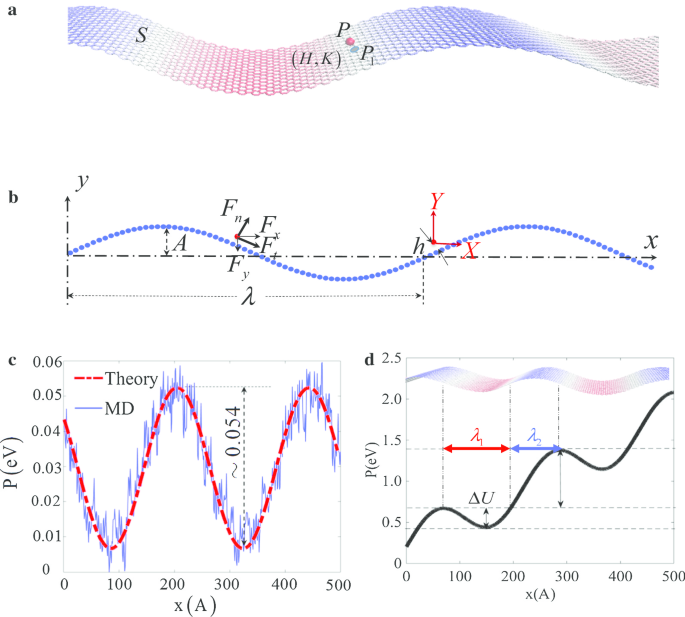
几何配置和电位分布。 一 波浪面S的3D模型 和一个外部粒子 P 与最近的点 P 1 在表面上； b 波浪形表面S的二维模型 和粒子 P; c 波状表面S相互作用势的比较 和一个外部粒子 P 由方程式(1)和MD模拟； d PXY 中的相对电位分布 坐标

那么，P之间的交互 和 S 证明可以写成基于 L-J 对势的平均曲率和高斯曲率的函数 [34,35,36],

$$\begin{aligned} U_{6 - 12} &=\frac{{4\pi \rho_{s} \varepsilon \sigma^{12} }}{{5h^{10} }}\left[ { 1 - hH + h^{2} H^{2} + \frac{{9h^{2} }}{16}\left( {H^{2} - K} \right)} \right] \\ &\quad - \,\frac{{2\pi \rho_{s} \varepsilon \sigma^{6} }}{{h^{4} }}\left[ {1 - hH + h^{2} H^{2} + \frac{{3h^{2} }}{4}\left( {H^{2} - K} \right)} \right] \\ \end{aligned}$$ (3 )

这里，点 \(P_{1}\) 是表面 S 上最近的点 到粒子 P , 和 H 和 \(K\) 分别是点 \(P_{1}\) 处的平均曲率和高斯曲率（图 2a）[20]。通过这种基于曲率的势能 [Eq. (3)] 已被用于解释许多微/纳米尺度的异常现象 [38, 39]，方程的可靠性。 (3) 在这种情况下，通过与上面给出的参数的 MD 模拟中的表面电位进行比较来验证，并显示在图 2c 中。

在分析波状表面对粒子P的影响之前 ，应该调查和考虑摩擦。粒子与波面之间的摩擦在纳米尺度上可能非常复杂 [39,40,41,42,43]。摩擦力的原始估计是通过 MD 模拟平面石墨烯层上粒子的运动来进行的，如附加文件 1：3 中所述。为了方便起见，这里采用平面而不是波浪形表面。这种近似值在附加文件 1:3 中估计，并结合了进一步的潜在水坑机制。使用上面给出的参数，摩擦力估计为 \(f =- 5.2 \times 10^{ - 13} \,{\text{N}}\).

那么，表面S之间的相对电位 和粒子 P 通过考虑摩擦进行研究。首先，建立相对波框坐标 \(PXY\)，如图 2b 中红色所示，它以波速移动，因此相对于行波保持静止。因此，行波在 \(PXY\) 中“冻结”。由于粒子相对于石墨烯不断向右移动，因此作用在其上的摩擦力将沿着表面不断向左。因此，相对波架势将是基于曲率的势减去摩擦所做的功，

$$P =U_{n} + f * x$$ (4)

代入基于曲率的势U n 和摩擦进入方程。 (4), 相对波框电位可以被评估并绘制在图 2d 中。

由于波坐标PXY 随行波移动，粒子P的初始位置 在势决定粒子的轨迹。假设粒子的初始速度P 为 \(v_{0}\) 且波速为 \(v_{{{\text{wave}}}}\)，基于图 2d 可以提出两个先决条件：粒子的初始位置 \( P\) 位于红色区域的潜在水坑\(\lambda_{1}\);初始波架动能满足 \(\frac{1}{2}m\left( {v_{0} - v_{{{\text{wave}}}} } \right)^{2} \le \Delta U\)。然后，粒子将无法跳出水坑，而是被困在水坑内并摇晃。从绝对坐标的角度来看，粒子\(P\) 将在势阱中振荡，但随着传播波以锁定在波速附近的速度继续移动，从而产生速度锁定效应。否则，如果粒子的初始位置 \(P\) 落在蓝色区域 \(\lambda_{2}\) 或相对初始动能 \(\frac{1}{2}m\left( {v_{ 0} - v_{{{\text{wave}}}} } \right)^{2}> \Delta U\)，粒子 \(P\) 不会停留在单个水坑内，而是向左跳跃到较低的水坑沿波架势面。从绝对坐标的角度来看，粒子将落后于传播的波，直到满足另一个力的平衡。这种平衡的一种可能性是粒子停止在石墨烯上移动，因此摩擦消失。有趣的是，在点燃 [21]。帕尼松等人。揭示当存在速度差时，行波会被粒子散射并提供推进力，表明粒子的最终速度将大于零。

为了表述和更好地说明我们的理论，通过牛顿运动定律进一步建立了粒子 P 的运动方程。作用在粒子P上的驱动力 包括法向力\(F_{{\text{n}}}\)和切向力\(F_{{\text{t}}}\)两部分，即（图2b），

$$F_{{\text{n}}} =\frac{{\partial U_{6 - 12} }}{\partial h}; \, F_{{\text{t}}} =\frac{{\partial U_{6 - 12} }}{\partial H}\nabla H + \frac{{\partial U_{6 - 12} }} {\部分 K}\nabla K$$ (5)

对于 L-J 势，原子之间存在吸引和排斥相互作用，外部粒子 \(P\) 将停留在高度 h 其中法向力\(F_{{\text{n}}}\)为零，高度h的确定计算 放在附加文件 1:2. 那么粒子\(P\)在\(x\)方向的运动方程为，

$$m\ddot{x} =F_{x} - f$$ (6)

这里，\(F_{x}\) 是\(x\) 方向上的切向力\(F_{{\text{t}}}\) 的分量（图2b）。计算方程(6) 给出粒子轨迹。对于正弦波表面，高斯曲率为零，平均曲率等于\(Ozx\)表面的曲线曲率，即\(K =0\)和\(H =\kappa\) [52]，代入等式(5) 代入(6)，粒子P的运动轨迹 可以数值求解。

锁定和解锁示例如图 3 所示。对于对应于图 2d 中锁定区域 \(\lambda_{1}\) 的初始位置（图 3a），比较理论和 MD 模拟结果的轨迹在图 3b 中。它表明粒子由于摩擦在很短的时间内停止在平坦的石墨烯表面上移动，而粒子在波面上继续向右移动。并且理论轨迹接近于MD模拟结果。这种趋势在图 3c 中得到了进一步证实，图中显示了十倍模拟时间的粒子速度。由于粒子落入锁定区，初始速度等于波速，它会在势阱中振荡，其整体速度等于波速，这与我们的推测是一致的。对于初始位置（图 3d）落入图 2d 中解锁区域 \(\lambda_{2}\) 的粒子，粒子在波面上的轨迹趋于一个常数（图 3e），并由速度分布。有趣的是，与平面石墨烯表面上的粒子运动相比，行波即使落在速度解锁区域也可以增强粒子的运动。图 3f 说明速度将在比模拟时间更长的时间内降低到零。更多示例在附加文件 1:3 中说明。

<图片>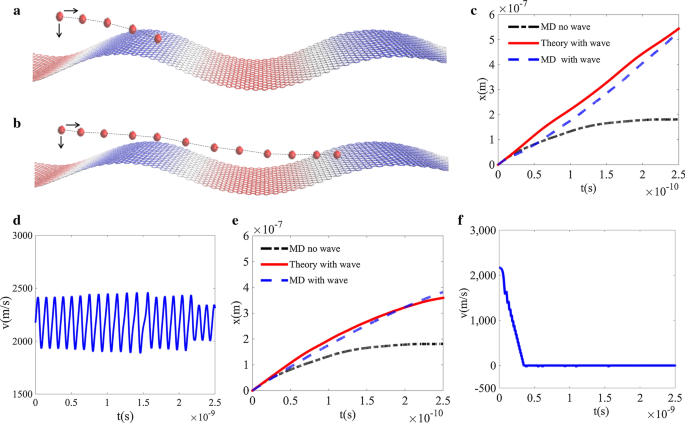

锁定和解锁的例子。 一 粒子如何落在波浪状石墨烯表面的速度锁定区域 \(\lambda_{1}\) 的示意图，其中初始粒子速度为 \(v_{0} =2175\,{{\text{m} } \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right.\kern-\nulldelimiterspace} {\text{s}}}\); b 粒子如何落在波浪状石墨烯表面的速度解锁区域\(\lambda_{2}\)上的示意图； c 通过MD模拟和理论的粒子轨迹，还绘制了平面石墨烯上的粒子轨迹以进行比较； d 粒子速度的时间演化方程。 (6); e 通过MD模拟和理论得到的粒子轨迹； f 粒子速度的时间演化方程。 (6)

根据势阱机理，粒子的锁速效应主要受势波面的支配。参数的影响可以基于势水坑理论进行讨论。显然，这些包括波长\(\lambda\)、幅度A ，频率 \(\omega\) 和 L-J 势参数。需要注意的是，在接下来的分析中，假设摩擦力对于不同的参数保持不变。不同波长A的电位分布 ，振幅 \(\lambda\) 和 L-J 电位参数 \(\varepsilon\) 分别如图 4 所示。图 4a 显示潜在的水坑深度随着 \(\lambda\) 的增加而减小，并且当波长超过临界值时将不存在速度锁定范围。此外，由于较低的频率 \(\omega\) 与较大的 \(\lambda\) 相关，所以速度锁定范围随着 \(\omega\) 的增加而减小。图 4b 说明了潜在的水坑深度随着 A 的增加而增加 ，幅度过小时锁速效果消失。值得注意的是，A 的比例 /\(\lambda\) 不应太大以防止损坏。通常，\(\lambda\) 和 A 当波或粒子的尺度增加时增加。为了研究规模效应，我们保持比率 \(\lambda\)/A 固定并检查变化的 \(\lambda\) 或 A 的影响 .图 4c 显示了潜在的水坑深度随着 \(\lambda\) 或 A 的增加而迅速减小 .这表明基于曲率的驱动力随着尺度的增加而迅速减小，因此粒子的速度锁定效应将在具有大尺度波的表面消失。对于 L-J 势参数 \(\varepsilon\)，证实了当对相互作用势强时速度锁定区域会更宽，当对相互作用势弱时速度锁定效应将消失（图 3）。 4d).

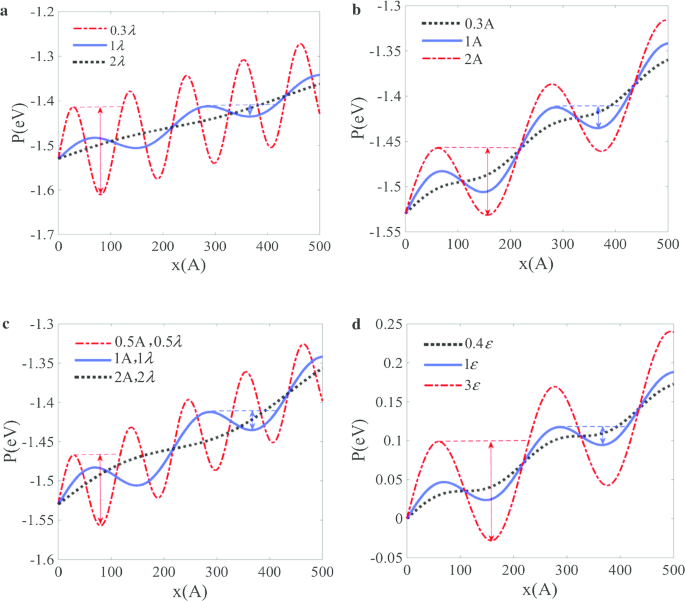
参数对潜在发布的影响：a 波长的影响； b 波幅的影响； c 波长与幅度之比的影响； d L-J势参数的影响

值得注意的是，其他二维纳米材料的刚度和 L-J 电位参数不同，这导致不同的频率和波速 [44]。根据参数分析，波状表面选择合适的波长和幅度会出现潜在的水坑。由于势阱是粒子在波状表面运动的前提条件，因此这种速度锁定效应也将在短程相互作用下对许多二维纳米材料层建立。

虽然本文讨论了一个粒子的运动，但它仍然是在热环境的框架内。势阱是粒子与表面耦合运动的必要条件。对于多个粒子，如果它们都位于潜在的水坑区域并满足先决条件，则它们将被捕获并随波状表面移动。根据参数效应，可以通过调节波长和幅度来控制粒子的运动。由于波长较小、振幅较大、频率较高的面波的锁速区较大，因此在波面的快速扩散也将得到增强。参数分析也符合许多其他文献中检测到的快速扩散规律。例如，Angelos 等人。指出扩散系数随着石墨烯表面波纹幅度的增加而增加[22]。他们证实波纹的幅度增加表明液滴对谷的偏好增加，这可以通过图 4b 来解释。当振幅增加到足够大时，速度锁定区可能会覆盖整个波长并增强扩散。此外，他们指出，谷的电位总是小于波峰的电位 [22]（图 4），这是对图 4 中波峰区域较低电位的响应。曹等人。研究了在表面波行进的情况下纳米通道内流体的流动，并证实速度随着振幅和频率的增加而增加[45]，这也与参数分析一致。

MD 模拟只能在很短的时间内反映性能，从潜在的水坑机制可以推导出这种锁速效应的更多潜在应用。例如，通过调整幅度和频率，可以实现几乎锁定或解锁的区域，可以驱动粒子移动或停止。需要注意的是，表面垂直方向的波浪运动可以转化为粒子的横向运动，类似于棘轮运动，可用于纳米机电系统。此外，由于粒子与表面的相互作用会影响运动，因此波状表面增强的轨迹对于不同对势的粒子会有所不同，从而导致短语分离。

结论

总之，我们证明了粒子和石墨烯层与行进表面波之间的独特关系，即速度锁定现象。通过MD模拟，证实了在一定条件下，粒子的速度可以保持在波速附近。建立了一个理论模型来阐明该机制，其中势面的水坑主导了锁定效应。基于该模型提出了锁定条件，即粒子的初始位置位于势坑中，初始动能不能驱使粒子跳出势坑。理论预测的粒子轨迹与MD模拟结果非常吻合。讨论了波长和幅度以及 L-J 电位参数的影响。该工作还为理解波浪表面上的快速扩散和传输以及短语分离的潜在应用提供了新的视角。

数据和材料的可用性

本研究期间生成或分析的所有数据均包含在这篇已发表的文章 [及其附加文件] 中。

缩写

MD：

分子动力学

vdW：

范德华

CNT：

碳纳米管

h-BN：

六方氮化硼

SWCNT：

单壁碳纳米管

L–J：

伦纳德-琼斯

LAMMPS：

大规模原子/分子大规模并行模拟器

REBO：

反应性经验键序

NVE：

微正则系综