用于增强转移电荷的基于针织结构的摩擦纳米发电机的表面形貌分析

介绍

先进的智能技术席卷全球，带来了一些新颖的柔性智能可穿戴设备，如健康追踪传感器[1, 2]、手势检测设备[3,4,5,6]、电子皮肤（E-skins ) [7, 8]、柔性电路 [9, 10] 和光纤可穿戴设备 [11, 12]。然而，电力补充具有重量大、转换效率低、环境污染严重、电池寿命短等缺点，成为电子发展的巨大限制。自 2012 年第一台摩擦纳米发电机 (TENG) 研制成功 [13] 以来，基于体积小、重量轻、材料多样、安全、环保 [14] 和高效等特点，它提供了一种有前途和有效的解决上述海峡问题的战略。随着通过接触带电和静电感应的耦合效应工作的 TENG 的迅速出现 [15]，它已成为从我们周围获得机械功率的一种理想方法 [16, 17]，特别是通过收集低频和不规则运动（包括风[18, 19]、水滴和人体运动、生物力学能量等[20,21,22]），实现物联网（IoT）中的数据传输[23,24,25]和电力补充[26]。对于可穿戴设备，纺织品因其结构保持性和抗疲劳性、柔软性、整体性和高孔隙率而被视为最佳基材。迄今为止，摩擦纳米发电机和传统纺织品的集成 [27,28,29,30,31,32,33] 是面向人的可穿戴设备的有希望的候选者之一，例如自供电柔性传感器 [34] 、可穿戴能量收集器和基于纺织品的能量存储系统。它还赋予传统纺织品功能性、智能性和高附加值。这些基于纺织品的电子设备满足了轻便、廉价、舒适、透气、便携、持久和日常使用可水洗的要求。此外，容易制作出色彩多样、图案丰富的纺织品，代表了智能纺织品的吸引力。特别是，具有小应变和大变形的针织纺织品对信号产生很敏感，因此非常适合用于柔性传感器、克服运动阻力和减少能量损失 [35]。此外，针织纺织品的摩擦和变形是常见现象，是构建摩擦纳米发电机的一个令人兴奋的观点。

众所周知，表面形态修饰是提高 TENG 输出性能的重要方法 [36,37,38,39]。大多数旨在增加可用的接触面积和表面粗糙度。有两种改变表面形态的主要方法，一种是表面蚀刻，另一种是表面复制。然而，使用昂贵的、有限的处理区域和多步骤制造技术来产生表面外观对于工业生产来说是困难的。在此，李等人。 [40] 研究了一种从砂纸上剥离的具有表面微结构的聚二甲基硅氧烷 (PDMS) 薄膜，这是一种制备表面差异粗糙度的单一工艺和低成本方法。实验结果表明，在 3D 光学表面轮廓检测到的 3000 级粗糙度下，生成的最大输出为 46.52 V。此外，过多的微结构会严重降低有效接触面，导致动力性能下降。 TENG的尺寸受到砂纸面积的限制，导致制造成本增加。如今，由于无需复杂的制造工艺和高成本即可形成丰富的表面外观[38]，纺织品结构正受到越来越多的关注。为了充分了解纺织品的表面外观，需要考虑独特成分和结构特征方面的一些因素，包括线外观、纺织品物理参数和针织结构。然后，Kwak 等人。 [41] 研究了拉伸过程中三种结构（包括平纹、双层和肋织物结构）的接触面积，并讨论了对提高潜力的贡献。值得一提的是，罗纹面料可以拉紧 30%，将接触面积扩大到 180 cm ² .根据存在的中间区域，罗纹织物可以得到很大的拉伸，这可以获得更大的增加接触面积的潜力。作为纺织品结构的主要元素，分析了毛圈的特性，这也是影响表面外观的重要因素。黄等人。 [42]重点关注纺织品基本参数（包括毛圈腿、毛圈沉降片和织物密度）的影响，以确认对输出性能的差异。大针密度织物基摩擦纳米发电机可以产生更高的电能，最大峰值功率密度为203 mW m ⁻² 在 80 MΩ 时，这使得有效接触面积更大。结果表明，各种织物结构的表面形态对电输出能力有影响。为了获得更多的能量以延长使用寿命，3D 双面互锁缝纫织物 [43] 由双针床单针织而成，其正面和背面的输出性能相同。此外，基于三维织物结构的TENGs可以产生3.4 mW m ⁻² 的高功率密度 在外部电阻为 200 MΩ 时，表明能量收集能力得到了提高。然而，上述表面外观对表面几何形状的描述很少，关于产生转移电荷的因素仍然缺乏具体的解释。没有通用的方法可以表征表面外观，需要找到对不规则形态的评价。因此，这是目前充分了解摩擦纳米发电机转移电荷的局限性。

表面分析的目的是表征纺织品的几何结构，可以用接触法和光学法两种方法进行测试[44]。接触法可以很好地描述表面形貌，但需要的时间要长得多，而且针会在表面留下痕迹。与接触法相比，光学法具有测量时间短、线束表面低、易于检测等优点，已被用于检测表面粗糙度。然而，虚假的间隙和高水平的噪声可能会降低对真实表面形态的判断。

数学工具是一种理论分析，可用于量化表面粗糙度的程度。这是一种评估不规则表面的新方法。对于这样的凹凸不平的表面，欧几里得几何的常规数学方法是无法使用的，因为很难判断定量的几何尺寸和测量精度，例如线段的长度和物体的重量。然而，分形几何，一种由 Mandelbrot 命名的描述不规则结构的方法，已被提供来解决这个问题并定义自然界中的不规则 [45]，例如泡沫的物理特性 [46] 和织物光滑度的评估 [47] .几乎所有的粗糙表面都可以分成一些自相似的部分，这些部分可以用一个非整数维数来描述，称为分形维数（D F）。基于各种几何曲面，D的值 在摩擦纳米发电机的设计中需要考虑和分析f对粗糙度和有效接触面积的影响，优化将人体运动转化为电能的能力。

在这里，在这项工作中，我们展示了基于针织结构的各种表面形态，这些结构被用作介电层之一。使用商品线和工业针织机制造了基于针织纺织品的 TENG，可以实现规模化生产和实际应用。为了模仿拍手动作，TENG 设计为接触分离工作模式 (CS)，这是最简单的工作机制。针织结构以两种方法形成，包括基于结构和基于形状的凸凹表面形态。由于针织结构的多样性，可以系统地研究和分析所得的表面外观，以确认表面形态与针织结构之间的关系。每种织物的 Df 都可以通过适当的分形原理计算出来，评价织物表面的粗糙度。通过拍打和释放运动，1*1肋表面外观的最大转移电荷可达91.66 nC，分形维数为0.99。一个有趣的现象表明，随着 D 的值 f 接近第一，转会费可以更高。最后，利用分形理论和针织结构可以提供一种有效的转移电荷定量评估方法，有望有助于设计出效率更高、工业化生产、成本低廉的针织纺织品TENG。

材料和方法

材料

常用的尼龙纱（dtex 600，安通科嘉纺织纤维制品有限公司）在整机（岛精机）上针织成15针/英寸的罗纹织物和凸纹织物两种株式会社，日本）。使用厚度为0.05 cm的聚四氟乙烯（PTFE）薄膜（辰奇电气技术有限公司）。弯曲和扭曲的电极为商用铜箔（深圳市标致胶带有限公司），厚度为0.06 mm，粘贴在针织物背面，用于转移极化电荷。

针织面料和针织纺织摩擦纳米发电机的制作

纬编技术作为代表性的针织方法可以轻松赋予织物高拉伸性 [48]、低成本和美观性能。凭借定位针织的优势，强力纺织品无需额外的缝纫技术即可融入服装中。设计了十种凹凸纹理，如表 1 所示。为了证明表面形态与转移电荷之间的关系，在纺织品表面编织了经线和横向线。因此，表 1 中描述了 10 种不同的纹理，其中前 7 个样品在表面上表现出纵向绳索，并且没有。 8，没有。 9，没有。 10个是横向凸面。在这里，结构由适合高效工业流程的电脑横机编织而成，纺织品能够定制定制规模。通过自有的设计系统，可以快速设计和轻松准备面料，特别是在设计复杂的图案时。所有织物均需在标准大气条件下放置24 h，使织物松弛至尺寸稳定的状态，以减少松弛收缩的影响，提高测试结果的准确性。然后，将相同尺寸的导电胶带粘贴在纺织品的背面。基于高极化纳米粒子，采用聚四氟乙烯薄膜作为其他介电材料。薄膜仍然粘附在一块铜箔上，传递电子迁移。对于 CS，导线已连接到两个摩擦模型，它们在垂直方向上移动。然后制作了基于CS的纺织品TENGs。

针织物的分形特征

并非所有自然物体都具有不完整的规则形状和边界，包括海岸线、雪花、云和树叶。因此，使用分形维数来描述不同方法产生的不均匀形态，是许多研究工作中确定的有效方法。有几种定义为分形维数的公式，包括豪斯多夫维数、计数框维数和类似维数等，它们是量化表面样式的关键参数。典型的分形维数是1904年首次提出的雪花状的Kohn曲线。三个自相似无穷大的区域是有限的，称为Kohn曲线，分形维数为1.2618。一般来说，分形维数可以用标度a来计算，它表示长度、宽度和面积。下面的公式可以表示这种关系：

其中 D f 是分形维数，表现在对数-对数图的斜率中。

不平整的表面分形维数，D f, 可以通过基于相似单元的相对尺寸分析的 Hausdorff 维数方法来确定。作为形成帘线面的因素，包含多个边数不同的微凸结构单元的凸区可表示为：

其中 M 是凸单元的个数，N 是重复的多个自相似单元，即凸单元的长度对整个样本的长度，D f 是凸起结构的分形维数。该方程是一个可以用来预测表面形貌的模型，所以：

特征化

使用Dino-lite边缘数码显微镜（AnMo电子公司）从照片图像测量针织物的密度。基于LabVIEW系统的自组装直线电机和静电计（Keithley 6514系统）对针织织物摩擦纳米发电机在接触和分离模式下的电信号进行操作。

结果与讨论

为了确认摩擦材料，摩擦电序[49]是重要的参考，它量化了不同常见材料的摩擦电极化。摩擦电序表示一侧显示获得电荷容量，另一侧具有高失去电子的能力，这已被定义为基本材料性能。为了获得出色的输出性能，选择了几种需要归因于具有相当距离的摩擦电系列的材料，从而增加了电位差。在此，一种是商用、低成本、优异的耐磨性和高带正电趋势（尼龙），另一种是带负电趋势（PTFE）。在这项工作中，我们选择了表面没有任何处理的 PTFE 膜。这里，唯一的因素是可以通过转移电荷的性能来分析的针织结构。另一个关键因素是电极材料是具有高柔韧性的铜箔，可以直接粘贴，这是一种简单的一步制造工艺。与贵金属银和金相比，铜箔的价格便宜，可以用来制造经济的产品。因此铜在智能设备的设计中被广泛用作柔性电路和电极。

目前，有四种通用工作模式操作的 TENG 对应于不同的电极结构和运动。 CS TENGs具有制造简便、材料选择丰富、垂直方向往复运动等优点，是第一个深入研究的具有收集一些生物力学能量的潜在能力，如拍手、步行和跑步。在这里，为了研究表面结构的影响原理，设计了基于针织织物 (KNG) 的摩擦纳米发电机，对应于尼龙织物和 PTFE 薄膜之间的接触和分离。摩擦纳米发电机的组装过程如图 1a 所示，由针织物、聚四氟乙烯膜和铜箔组成。柔性针织物在任何方向的卷曲（图 1bi）、弯曲（图 1bii）、悬垂（图 1biii）和折叠（图 1biv）能力方面的多功能性以各种规模定制如图 1b 所示。 KNG 可根据应用位置的要求和服装的美观度进行设计。针织结构的多样性已经被编织成不同的表面外观，然后这些织物表面的照片如图1c所示。

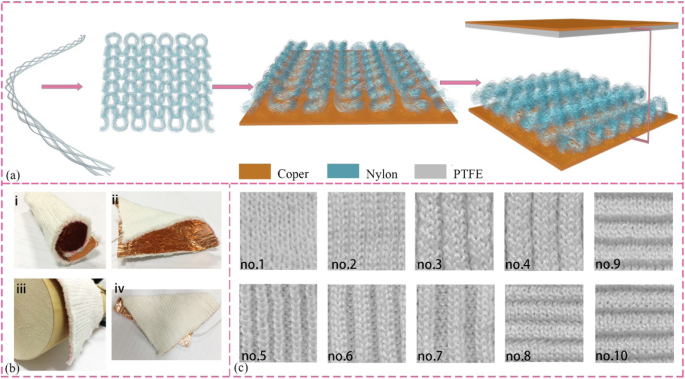
示意图制备、KNG的特性和针织结构。 一 KNG的制造过程。 b 各种变形下的 KNG 图像。我，卷曲的； ii、弯曲； iii、披着； iv、折叠。 c 所有的编织结构，从1号到10号

KNG 的运行机制简单地呈现在图 2a 中。为了测量转移电荷，线性电机的最大距离和运动频率分别设置为 10 cm 和 0.3 Hz，以模拟拍手运动。至于常见的监测，开路电压 (Voc)、短路电流 (Isc) 和转移电荷 (Qsc) 由机械线性电机测量。在原始状态下（图 2 ai），由于静电感应和电荷守恒，尼龙织物产生正电荷，聚四氟乙烯薄膜带负电荷。当设备被按压时（图 2 aii），两个接触面之间的间隙收缩将导致正电荷在粘贴在 PTFE 上的电极中积累。电子从外部电路流出以平衡电位差。值得注意的是，由于两种介电材料都是绝缘体，因此可以在接触区域的表面上保持等量的电子（图 2 aiii）。随着 PTFE 向后移动（图 2aiv），该过程发生逆转，尼龙织物和 PTFE 之间的电将再次获得平衡，反映了电荷的中和。因此，电子将因电位差而回流。在这种情况下，KNGs 可以产生 Isc 和 Voc，它们具有周期性变化的特征，如图 2b 和 c 所示。在图2b和c中，插图是在一个循环中描述的放大图。

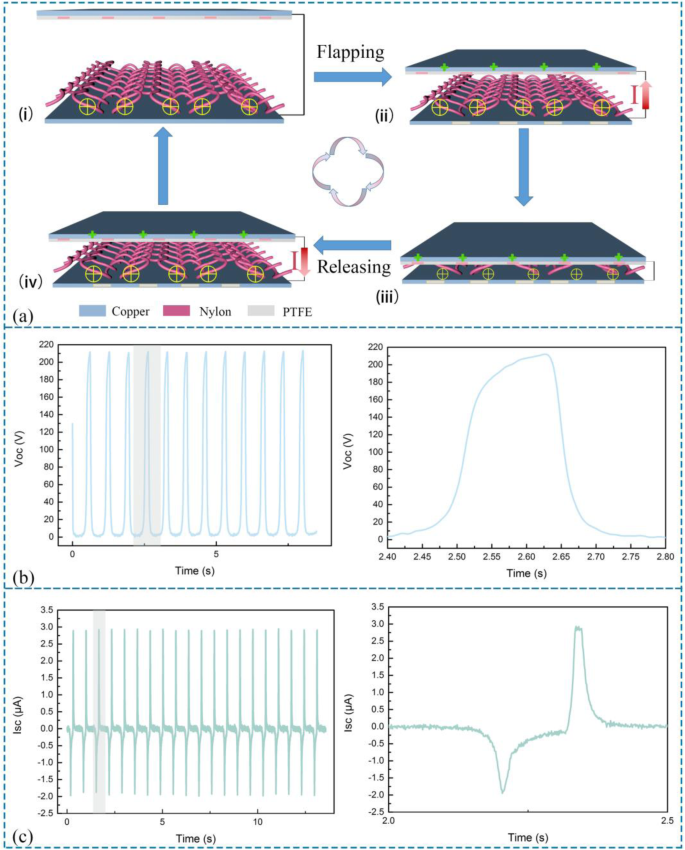
KNG的电力工作机制与输出性能。 一 使用尼龙织物与聚四氟乙烯构件接触的 KNG 操作机制。 b KNG 的 Voc 和放大的图像为一个周期。 c KNG的Isc和一个周期的放大图

为了在纺织品表面制作凸出结构，有两种方法，包括结构设计和成型，如图3所示。 结构设计取决于面环线迹的不同比例和反面环针。总共设计了七种肋型，包括 m*n (m =n =1, 2, 3, 4) 在图 3a 和 2*m (m =1, 2, 3, 4) 如图 3b 所示。由于面环纵行倾向于在反向环纵行上方和前面移动，因此肋具有垂直的绳索外观；那么，绳子的最大高度可以达到0.2 cm。 m*n (m =n =1, 2, 3, 4) 可以通过每侧的脸环交替纵行来平衡，因此剪裁后它可以平放而不会卷曲。并且纺织品的两面都是相同的外观，如图 3e 所示。但是，2*m 的肋条结构中的正面和反面环的比例不同，出现了一个区分面，如图3f 所示。此外，罗纹织物的拉伸过程分为两个阶段，包括将两侧的反向横纹相互交织，直到被拉伸以露出中间的反向线圈横纹，然后整个线圈继续拉伸至同等宽度的两倍单一面料。因此，与平纹织物相比，罗纹织物在接触分离工作模式下有可能增加收获拍打和拉伸运动（横向和纵向）的可拉伸能力。另一种建立凸起结构的方法是形状变形，其中在n的表面形成空气层。 (n =4, 5, 6) 图 3c 所示的纺织品。横截面积的厚度在0.15到0.3 cm范围内。空气层的特点是突出的拱形结构，可以在触发运动时为加速电子分离提供一定的空间。综上所述，针织纺织品通过电脑横机设计，可实现针织定位精度，形成整件服装，将智能材料完美融入布料。这种针织技术命名法已经在图3d中进行了标注，正确地描述了结构特征。

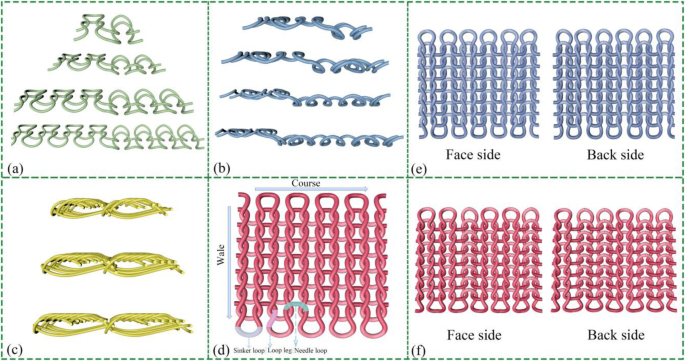
针织结构的示意图特征和组成部分。 一 m*n 肋的特性。 b 2*m 肋的特性。 c 一些针横绳的特点。 d 针织技术命名法。 e 1*1 肋条结构中正面和背面的图像。 f 2*1肋条结构正反面图片

以前的工作[42]证明了正面的有效接触面积远大于纺织品背面；结果转移电荷是背面输出性能的两倍。这是因为针环的长度比沉降环的长度长。因此，为了提高输出性能并仅产生一个影响因素，接触凸起结构由面侧环组成。 KNG 的输出取决于凸单元的数量绘制在图 4 中。形成了所有实验纺织品的接触面积随着凸起单元的数量而减少的下降趋势。此外，更显着的电荷按 1*1 肋、2*1 肋和四个针状结构（每条线的第一个点）的顺序排列，其值为 91.66 nC、90.19 nC 和分别为 69.64 nC。

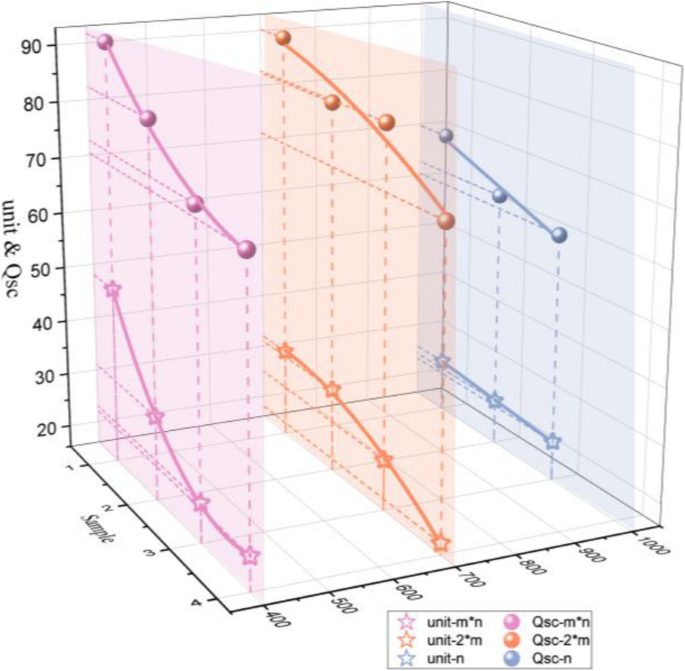
输出性能随凸单元数量变化

然后，研究了在不同的纬密度、面侧单元的数量和结构方面具有不同表面形态的针织结构。十种针织纺织品的所有参数都经过测试并记录在表 2 中。值得注意的是，由于在分析 1-7 号样品时，帘线外观沿垂直方向增长，因此横列密度始终保持不变。因此，作为需要讨论的主要因素的纵行密度是指不同针织结构的特点。很明显，面环和反向环在1-4号中的比例相同，约为50%。基于双线迹编织，这些纺织品无论正面还是背面都显示出相同的结构。与样品编号相比，平均厚度显示更高。 5-7 由不同数量的面针和备用针组成。纹理编号4 拥有最大的重复单元，其纹密度是 no 的两倍。 1.然而，实际面料上的正面单元数量比没有下降近一半。 1.这是因为更多的沉降片环相互拉伸，以便形成柱状外观。随着针织单元的增加，柱的直径和织物的厚度增大，从而减少了正面单元的数量和触发运动时的有效接触面积。在不同比例面和反圈的罗纹结构方面，外观表现出明显的单面结构特征，针织重复单元增多。同时，没有的腰围密度。 7 和 no 一样大。 1 和没有。 5，但面环单元的数量有明显差异，因为针织单元的数量是六个环，远远超过没有。 1（2 个循环）和没有。 5（3个循环），所以输出性能低于no。 1 和没有。 5.因此，罗纹针织物没有。 1 表示 nos 中最多的面部循环单元。 1-10在接触-分离运动中。

另一方面，形状型针织纺织品通过不同数量的线圈组装成整个织物，形成拱形结构。由于帘线长度方向是水平方向，织物的纵行密度在横向上表现出近似稳定。拱形结构提供了一种在表面分离电荷的方法，其具有中空的内部空间。因此，收集浪费的机械能量的效率得到了提高。通常，为了提高输出性能，拱型采用具有完美弹性和耐用性的柔性材料制成，例如硅基板，但很难在工业针织机上编织以满足商业需求。在之前的研究[24,41,50]中，当谈到拱形结构是基于针织纺织品时，需要缝制或贴胶带，这是一个复杂且耗时的过程。我们展示了一种通过整个成型技术制成的针织拱形纺织品，无需二次制造，具有高生产效率。在水平帘线结构中，与高度分别为 0.15 cm 和 0.2 cm 的四针和五针水平帘线结构相比，0.3 厘米高度显示出最低的电荷输出，这可能受到针织纺织品低刚度的影响两端固定的大距离。最高的凸面形状难以在力压下保持拱形并恢复到原始形状，从而导致部分电荷被中和。因此，拱高的降低可以提高凸结构的耐受性。然而，这种形状类型的电线减少了有效接触面积，这是一种线型，比实际接触面积小，降低了电输出的性能。

环具有不规则的结构，因此对其几何特性（例如针迹尺寸和表面形状）的评估具有挑战性。为了识别环路的不规则性，不能利用作为整体维度的传统评估。建议使用分形理论来分析我们周围环境和自然中不规则的类别。所提出的分形维数概念是展示复杂形态的极好工具，可呈现纺织品表面的规则、复杂性和粗糙度。因为所有的分形都不是完全自相似的，所以用数学计算来论证几何构型。为了理解针织结构的表面，一些图像将图 5d 中携带的信息可视化。如图5d所示，可以从不同的角度直观地观察凸面的特征，这是确认凸起形态的证据。

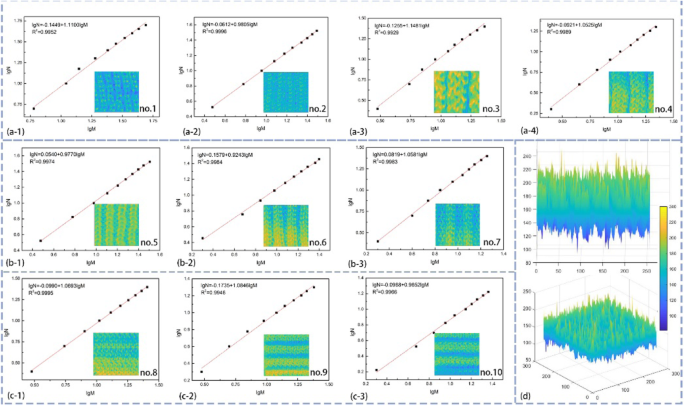
针织纺织品的拟合曲线和一些视觉图像。 一 m*n 肋结构。 b 2*m 肋结构。 c 有的针横绳结构。 d 不同方面的视觉图像

The uneven surface has been formed with the knit structure designed caused by the yarn morphology and structure design. The fractal geometry is an efficient calculation for evaluating the textile surface and understanding the characteristic of knitted structures and ability of triboelectric charge generation. In fact, with the increase of the raised unit, it can improve the uneven knitted textile owing to the surface shape modified. Although all of the knitted textile own convex structures in longitude and transverse direction, the degree of similarity is still not confirmed that is the significant reference value for whether using fractal dimension successfully or not. To estimate the feasibility of fractal dimension, all of the knitted fabrics are calculated through measuring the width of the convex unit, the size of loops in length, and width when textiles stay in stable size. Figure 5 a, b, and c show the fitting curve of fractal dimension of nos. 1–10 type fabrics, and slope of a line means the fractal dimension. The existence of the relationship is found in convex structures of the ten different types of knitted textiles, which confirms the fractal characteristic of ten knitted fabrics. Therefore, the fractal theory applied in the analysis of diversity knit structure that is practicable.

Figure 6a–f illustrates the generated Isc and Voc based on the practical applications of contact and separation working KNGs, based on the structure types and shape types. There is a trend that a decrease with the knit unit increases about the Isc and Voc as shown in Fig. 6a–f. This is because the Isc is changed with the effective contact area which is affected by knit structures.

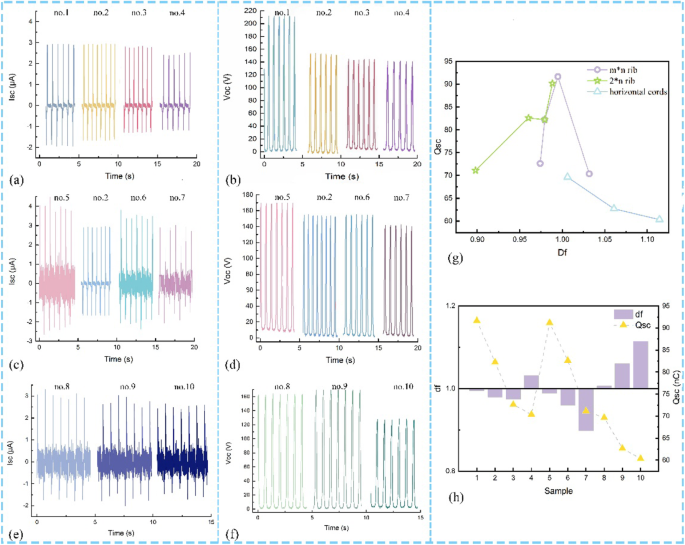
Schematic illustration of fractal dimension and generated Isc and Voc. 一 The Isc of m*n rib. b the Voc of the m*n rib. c The Isc of 2*m rib. d The Voc of the 2*m rib. e The Isc of n type. f The Voc of n type. g The Df-transfer charge curve. h The F value curve

When calculating the D f of various knit structures, the investigated knit structure states that the different knit structures have an unequal value which is non-integral dimension due to the different components of convex as demonstrated in Fig. 6g. As for Fig. 6g, this is the image of the transfer charge versus fractal dimension curve of diversity structures. The rib structure presents desirable output performance and the fractal dimension near the value of one. The TENGs based on structure-type knitted-textiles have a higher transfer charge than shape type and the value of D f about the m*n rib type, 2*n rib type, and n type is in the range of 0–2, 0–1, and 1–2, respectively. Generally, the fractal dimension symbolizes the extent of surface roughness which is the roughness increasing with the large D F。 However, the shape-type fabrics are designed in horizontal cord with small line-contact area, so the roughness has little influence on the transfer charge.

In order to demonstrate the influence on D f of convex structure homogeneity in rib structures, the random side length is chosen and calculated. The result exhibits as follow:

其中 a is the length of the whole fabric, b is the width of the convex unit and is equal to the width of the whole fabric, l is the length of the convex unit, M is the number of the convex unit, N is the repeated multiple of self-similar units that is the length of convex units to the length of whole samples, and ε is the proportion of face loop and reverse loop, meaning the uniform of the convex distraction.

Then, the calculation of M and N can be used in the formulation (1-3), the result shows that obtained D f is not the same with the D f that is calculated based on the length of actualmeasurement as shown in Table 3. No matter how the raised structure is distributed, the value of D f is affected by the practical length and number of cords.

It is noted that the fractal dimension of the 2*1 rib structure is close to the 1*1 rib reach at 0.99, and thus, the transfer charge is much the same as shown in Fig. 6g. The generated electrical-output performance shows the highest when the D f is near the value of one. That has provided one guess if the fractal dimension can evaluate the surface morphology and character the output performance. To investigate the correlation of fractal and transfer charge, the difference between the fractal dimension and the value of one (named F value) has been illustrated in Fig. 6h. The operating results show a trend that is decreased F value can boost the much higher Voc, taking evidence for potential application of fractal dimension.然而，F value is regarded as an evaluation of the roughness structures, which needs to consider the properties of the primary loop of the structure. Then, the influence on transfer charge is discussed comprehensively. The sample of no. 4 and no. 6 has a similar F value, but the massive difference exists on both of output performance. The surface morphology of no. 4 shows the planar structure due to the same number of face and reverse loops, so the transfer charge is low.但不是。 6 has prominent appearance due to the reverse loops over the face stitches and the generated large transfer charge when contacting and separating. Therefore, the selection and design of the knitted structure of the textile based on the F value highly improved the generated total electrical charge, which is an indispensable requirement for construct a high-effective flexible self-power device based on the knitted textiles.

结论

We have demonstrated that the knitted textile with high flexibility and excellent transfer charge can be applied in flexible TENGs for harvesting irregular and low-frequency biomechanical energy, which owns an outstanding output performance. To identify the relationship between surface morphology and output property, fractal theory has been used to quantify the surface geometry and used to evaluate its influence on the transfer charge ability of surface appearance. Different knit structures have been fabricated that can analyze their impact on energy harvesting. From the aspect of the knitted unit, the result shows that the maximum output of 1*1 rib structure can reach at 213 V with the minimum knitted unit. In addition, to further understand the working mechanism and the geometry of contact area, the various knit structures have been illustrated in a fractal dimension that is distinct from traditional dimension. Through calculation, different knitted structures with identical knit units can be used to obtain fractal dimension with the same knit units. The generated electrical output can be increased with the fractal dimension close to the value of one. Therefore, the difference between the fractal dimension and the value one can be used in the evaluation of transfer charge ability according to the irregular surface. In the near future, it is expected that an evaluation for generating output ability based on fractal theory in constructing a triboelectric nanogenerator, obtaining maximum output performance to optimize the flexible self-power system for harvesting wasted human motions in our daily life will be investigated.

数据和材料的可用性

本研究期间生成或分析的所有数据均包含在这篇已发表的文章中。

缩写

E-skins:

Electronic skins

IoT:

Internet of Things

PDMS：

聚二甲基硅氧烷

TENG:

摩擦纳米发电机

聚四氟乙烯：

聚四氟乙烯

Df:

Fractal dimension

CS：

Contact-separate working mode

KNG:

The triboelectric nanogenerator based on knitted textile

Voc:

The open-circuit voltage

Isc:

短路电流

Qsc:

Transfer charge

F value:

The difference between the fractal dimension and the value of one