使维恩图看起来像卡诺图

以圆 A 开头 在矩形A'宇宙中 在下图 (a) 中，我们将维恩图变形为几乎是卡诺图。

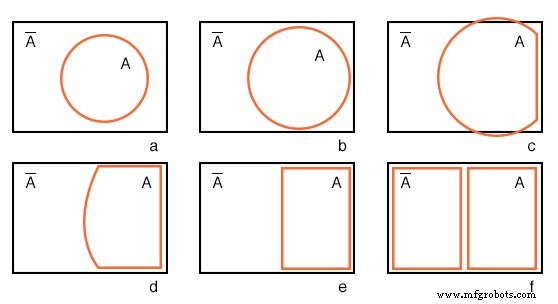
我们展开圆A 在（b）和（c）处，符合矩形A’宇宙 在 (d) 处，并更改 A 到（e）处的矩形。 A 之外的任何东西 是 A' .我们为 A' 分配一个矩形 在（f）。此外，我们不在卡诺图中使用阴影。到目前为止，我们所拥有的类似于 1 变量卡诺图，但实用性不大。我们需要多个变量。

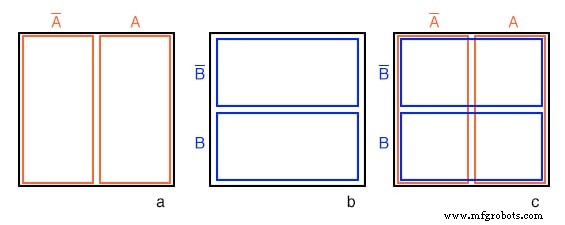
上图 (a) 与之前显示 A 的维恩图相同 和 A' 上面除了标签 A 和 A' 位于图表上方，而不是在相应区域内。想象一下，我们经历了一个类似于图 (a-f) 的过程来得到 B 的“方形维恩图” 和 B' 正如我们在中间图（b）中所示。

我们现在将叠加图 (a) 和 (b) 中的图以获得 (c) 处的结果，就像我们对维恩图所做的一样。我们这样做的原因是为了我们可以观察到两个重叠区域可能共有的东西——比如 A 重叠B .图(c)右下角单元格对应AB 其中 A 重叠B .

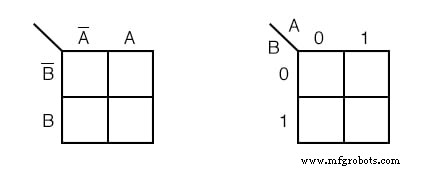
我们不会浪费时间像上面 (c) 那样绘制卡诺图，而是在左上方绘制一个简化版本。 A’ 下两个单元格的列 被理解为与 A’ 相关联 , 和标题 A 与其下方的单元格列相关联。以 B' 为首的行 与它右侧的单元格相关联。

以类似的方式B 与它右侧的单元格相关联。为简单起见，我们没有像维恩图那样清楚地描绘各个区域。

右上方的卡诺图是大多数文本中使用的替代形式。变量名称列在对角线旁边。

A 对角线上方表示变量 A （和A' ) 分配给列。 0 是 A' 的替代品 , 和 1 A 的替代品 . B 对角线下方与行相关联：0 对于 B' , 和 1 对于 B

示例：

标记布尔表达式AB对应的单元格 在上面带有 1 的卡诺图中

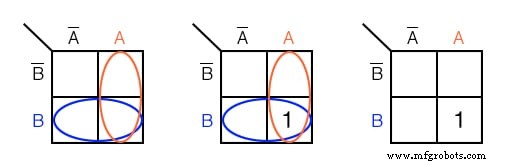
解决方案：

阴影或圈出与 A 对应的区域 .然后，将 B 对应的区域阴影或包围起来 .两个区域的重叠为AB .放置一个 1 在这个单元格中。我们不一定将 A 括起来 和 B 区域如左上。

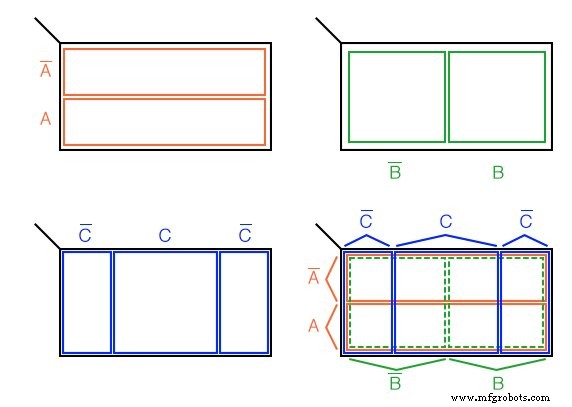
3 变量 K-map

我们在上面开发了一个 3 变量卡诺图，从类似区域的维恩图开始。对于A’，宇宙（黑色矩形内）被分成两个狭窄的矩形区域 和 A .变量 B' 和 B 把宇宙分成两个正方形区域。 C 占据矩形中间的一个正方形区域，带有C’ 在 C 的每一侧分成两个垂直矩形 方形。

在最后一张图中，我们叠加了所有三个变量，试图清楚地标记各个区域。没有彩色印刷的区域不那么明显，与其他三幅图相比更为明显。

这个 3 变量 K-Map （卡诺图）有 2 ³ =8 细胞 ，地图内的小方块。每个单元格由三个布尔变量（A、B、C ）。例如，ABC’ 唯一选择最右下角的单元格 (*)，A'B'C' 选择最左上角的单元格 (x)。

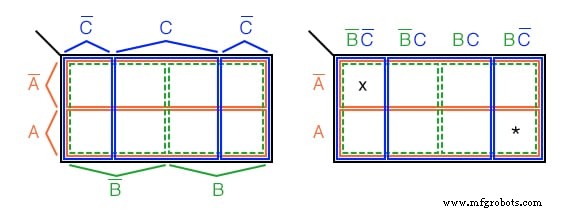
我们通常不会像左上图那样标记卡诺图。尽管该图清楚地显示了 4 个单元格区域的单个布尔变量的地图覆盖率。

卡诺图的标签如右图所示。每个单元格仍然由一个 3 变量的产品术语唯一标识 , 布尔 AND 表达。例如，ABC’ 遵循 A 向右排和 BC' 列向下，都在右下方的单元格 ABC' 处相交 .见上图（*）。

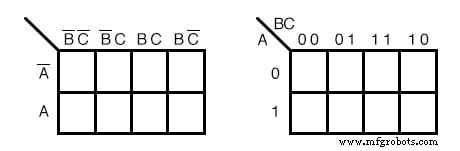
三变量卡诺图的上述两种不同形式是等价的，是它所采用的最终形式。右边的版本更容易使用，因为我们不必写下这么多布尔字母表头和补码，只需1和0 使用右边的地图形式，在一些文本中寻找左边的.左边的列标题 B'C', B'C, BC, BC' 相当于 00, 01, 11, 10 在右侧。行标题 A, A' 等价于 0, 1 在正确的地图上。