维恩图上的布尔关系

第四个例子有 A 部分重叠B .不过，我们将首先查看下面所有阴影区域的整体，然后仅查看重叠区域。让我们为上面的区域分配一些布尔表达式，如下所示。

左下方是 A 的红色水平阴影区域 . B 有一个蓝色的垂直阴影区域 .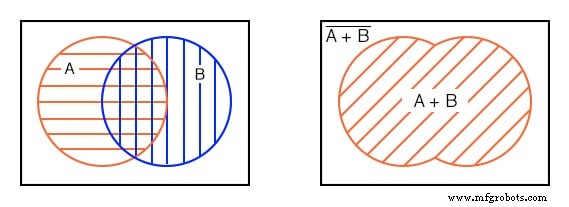

如果我们查看两者的整个区域，无论阴影样式如何，所有阴影区域的总和，我们都会得到右上方的插图，对应于包含的 OR A, B 的函数。布尔表达式为 A+B .

这由 45 ^o 表示 孵化区。阴影区域之外的任何内容都对应于 (A+B)-not 如上图所示。让我们继续看第四个例子的下一部分。

查看带有重叠圆圈的维恩图的另一种方式是只查看 A 共有的部分 和 B ，左下方的双阴影区域。此公共区域的布尔表达式对应于 AND 功能是AB 如下右图所示。请注意，除双影线 AB 之外的所有内容 是AB-不是 .

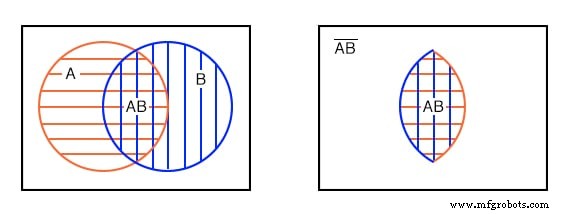
请注意，A 的一些成员 ，上面是(AB)’的成员 . B的部分成员 是(AB)’的成员 .但是，(AB)’的成员都没有 位于双阴影区域AB .

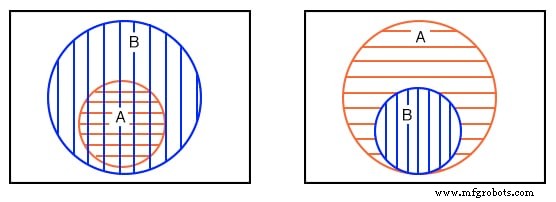
我们重复了左上方的第二个例子。您之前绘制的第五个示例在右上方提供以进行比较。稍后我们将找到完全包含在卡诺图中另一组中的偶然元素或元素组。

接下来，我们展示了一个包含补变量的布尔表达式的开发过程。

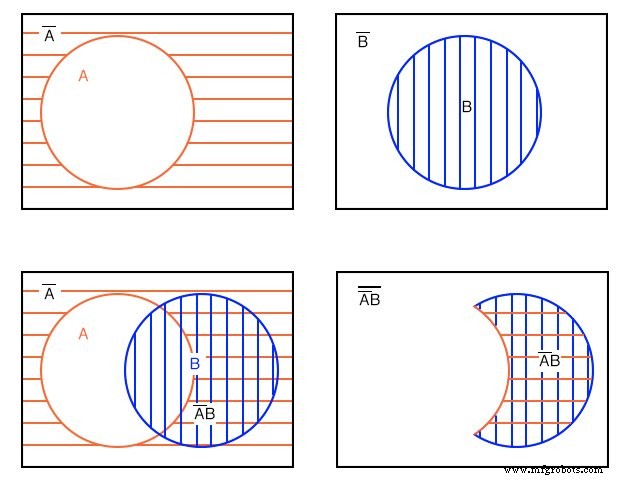
示例： （上）

显示 A'B 的维恩图 （A-不是 AND B）。

解决方案： 从左上角开始，我们有红色的水平阴影 A' （A-不是），然后，右上角，B .接下来，左下角，我们形成 AND 函数 A’B 通过重叠前两个区域。大多数人会以此作为所举例子的答案。

然而，只有双阴影 A'B 为清楚起见，显示在最右边。表达式 A'B 是 A’ 所在的区域 和 B 重叠。 A'B 之外的清晰区域 是 (A'B)' ，这不是所提出的例子的一部分。

让我们尝试类似布尔OR 功能。

示例： 找到B'+A

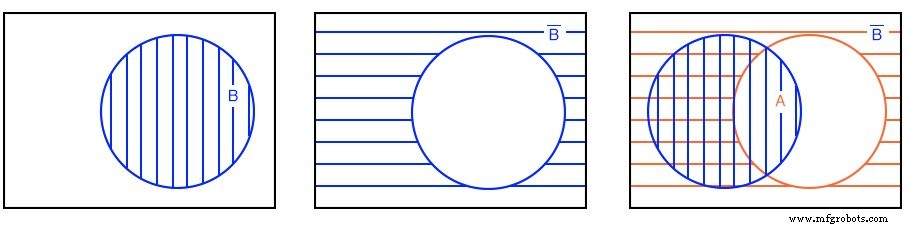
解决方案： 在右上方，我们从 B 开始 这是对 B' 的补充 .最后我们覆盖A 在B'之上 .由于我们有兴趣形成 OR 函数，我们将查找所有阴影区域，而不管阴影样式如何。因此，A+B’ 是右上方的所有阴影区域。为清楚起见，它显示为左下方的单个阴影区域。

示例： 找到(A+B’)’

解决方案：

绿色 45 ^o A+B’ 阴影区域是上一个示例的结果。继续到，(A+B')' ,本例，在左上方，让我们找到 A+B’ 的补码 ，也就是左上方对应(A+B’)’的白色清晰区域 .

请注意，我们在右侧重复了 AB' 上一个示例的双阴影结果，用于与我们的结果进行比较。 (A+B’)’对应的区域 和 AB' 以上左右分别是相同的。这可以用德摩根定理和双重否定来证明。

这提出了一个观点。维恩图实际上并不能证明任何事情。形式证明需要布尔代数。但是，维恩图可用于验证和可视化。我们已经用维恩图验证并可视化了德摩根定理。

示例：

什么是布尔表达式A'+B' 看起来像维恩图？

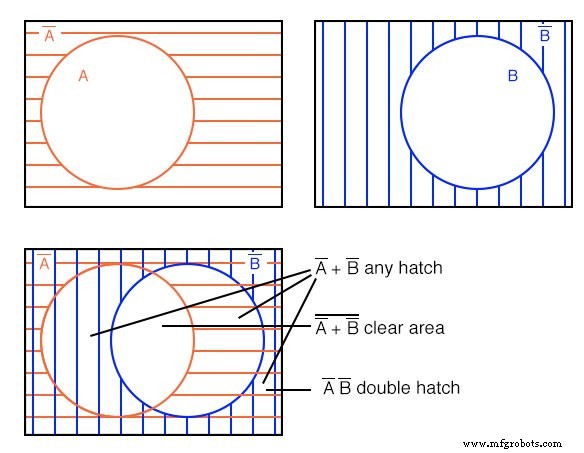
解决方案： 上图

从红色水平影线 A' 开始 和蓝色垂直阴影 B' 多于。如图所示叠加图表。我们仍然可以看到 A' 红色水平舱口叠加在另一个舱口上。它还填充了过去 B 的一部分 (B-true) 圆，但只有 B 的那部分 A 不常见的空心圆圈 开圈。

如果我们只看 B' 蓝色垂直影线，它填充了开放的那部分 A B 不常见的圆 .任何带有阴影的区域，无论类型如何，都对应于 A'+B' .也就是说，除了中心的空白区域之外的所有东西。

示例：

什么是布尔表达式(A'+B')' 看起来像维恩图？

解决方案： 上图，左下

看着中心的白色空地，一切NOT 在之前的 A’+B’ 解决方案中 , 即 (A'+B')' .

示例： 证明 (A'+B')' =AB

解决方案： 下图，左下

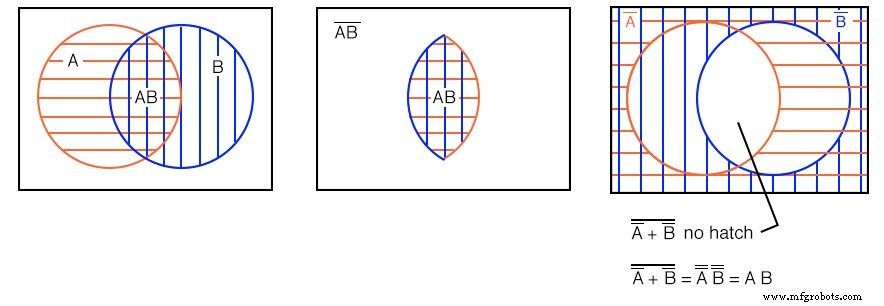
我们之前在右上方的图表中显示，白色的开放区域是 (A'+B')' .在前面的示例中，我们在 AB 的交叉点（叠加）处展示了一个双阴影区域 .这是这里重复的左中图。

比较两个维恩图，我们看到这个开放区域，(A'+B')' , 与双阴影区域 AB 相同 （A 和 B）。我们也可以证明(A’+B’)’=AB 由 DeMorgan 定理和双否定如上所示。

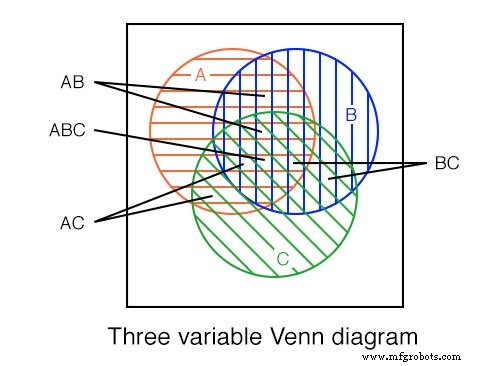
我们展示了上面带有区域 A 的三变量维恩图 （红色水平），B （蓝色垂直）和，C (绿色 45 ^o ）。在最中心注意所有三个区域重叠表示布尔表达式 ABC .

还有一个较大的花瓣形区域，其中 A 和 B 布尔表达式AB对应的重叠 .以类似的方式A 和 C 重叠产生布尔表达式AC .还有B 和 C 重叠产生布尔表达式BC .

查看上面由 AND 表达式描述的区域大小，我们看到区域大小随关联 AND 表达式中变量的数量而变化。

• A , 1-variable 是一个大的圆形区域。
• AB , 2-variable 是一个较小的花瓣形区域。
• ABC , 3-variable 是最小的区域。
• AND 项中的变量越多，区域越小。