不关心卡诺图中的单元格

到目前为止，我们已经考虑了完全指定输入条件的逻辑归约问题。也就是说，一个 3 变量真值表或卡诺图有 2 ⁿ =2 ³ 或 8 个条目，一个完整的表格或地图。

对于一些现实世界的问题，并不总是需要填写完整的真值表。我们可以选择不填写完整的表格。

例如，在处理编码为四位的 BCD（二进制编码的十进制）数字时，我们可能不关心任何高于 (0, 1, 2…9) BCD 范围的代码。十六进制数（Ah、Bh、Ch、Eh、Fh）的4位二进制码不是有效的BCD码。

因此，如果我们不关心，我们不必在真值表或 K-map 的末尾填写这些代码。

我们通常不会关心填写这些代码，因为只要我们只处理 BCD 编码的数字，这些代码（1010、1011、1100、1101、1110、1111）就永远不会存在。这六个无效代码不在乎 就我们而言。

也就是说，我们不关心我们的逻辑电路产生什么输出，因为这些不关心。

不在乎

卡诺图或真值表中的无关紧要可能是 1 s 或 0 s，只要我们不关心我们从不期望看到的输入条件的输出是什么。我们用星号 * 在正常 1 中绘制这些单元格 s 和 0 s.

在形成单元格组时，将不关心单元格视为 1 或 0 ，或忽略不关心。

如果它允许我们形成一个比没有不关心的情况下可能形成的更大的群体，这将很有帮助。不需要将所有或任何不关心的人分组。

如果可以简化逻辑，则仅在组中使用它们。

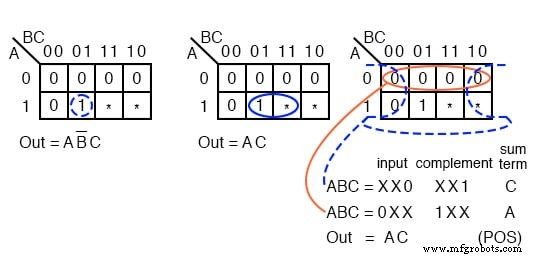
以上是所需输出为 1 的逻辑函数示例 对于输入 ABC =101 在 000 到 101 的范围内 .我们不关心其他可能的输入 (110, 111) 的输出是什么 .将这两个映射为不关心。我们展示了两种解决方案。

右边的解决方案 Out =AB'C 是更复杂的解决方案，因为我们没有使用无关单元。中间的解决方案 Out=AC 不那么复杂，因为我们将一个不关心的单元与单个 1 分组 两人一组。

第三种解决方案，右侧的“乘积”，是将 a don't care 与三个零组成一组四个 0 的结果 s。这是相同的，不那么复杂，Out=AC .

我们已经说明不关心单元格可以用作 1 s 或 0 s，以有用的为准。

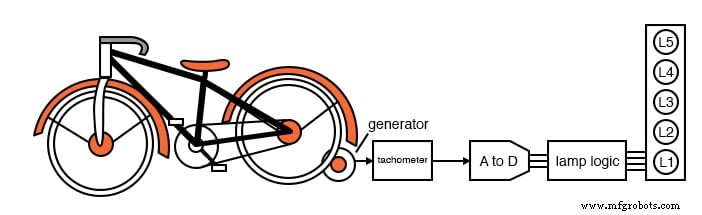
闪电州立大学的电子课程被要求为当地科学博物馆的固定自行车展览构建灯逻辑。当骑手提高蹬踏速度时，条形图显示器上的灯会亮起。

没有灯会因为没有运动而点亮。随着速度的增加，下方的灯 L1 亮起，然后是 L1 和 L2，然后是 L1、L2 和 L3，直到所有灯以最高速度亮起。一旦所有灯亮起，速度的进一步增加将不会对显示产生任何影响。

连接到自行车轮胎的小型直流发电机输出与速度成正比的电压。它驱动一个转速计板，该板限制所有灯点亮的最高速度时的电压。速度的进一步提高不会使电压超过这个水平。

这很重要，因为下游 A 到 D（模拟到数字）转换器输出一个 3 位代码，ABC , 2 ³ 或 8 码，但我们只有五盏灯。 A 是最高位，C 最低有效位。

灯逻辑需要响应A到D中的6个代码。对于ABC=000 ，没有动作，没有灯光。对于五个代码(001 to 101) 灯L1、L1&L2、L1&L2&L3，随着速度、电压、A转D码（ABC）的增加，直到所有灯都会点亮。

我们不关心对输入代码的响应 (110, 111) 因为由于转速计块的限制，这些代码永远不会从 A 到 D 中出来。我们需要设计五个逻辑电路来驱动五个灯。

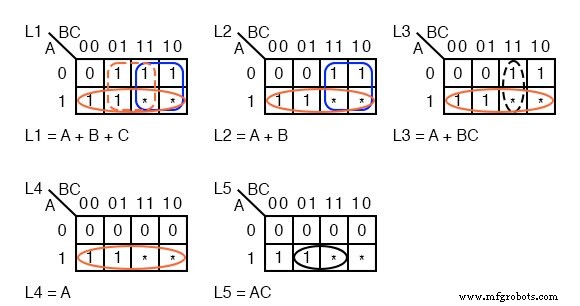
因为，ABC=000 的灯都不亮 从 A 到 D，输入一个 0 在单元格 ABC=000 的所有 K 图中 .由于我们不关心永远不会遇到的代码 (110, 111) , 在所有五个 K 图中的这两个单元格中输入星号。

灯 L5 仅在代码 ABC=101 时点亮 .输入 1 在那个单元格和五个 0 s 进入 L5 K-map 的剩余空单元格。

L4 最初会亮起代码 ABC=100 ，并且对于任何更大的代码将保持点亮，ABC=101 ，因为当L5点亮时，L5以下的所有灯都会点亮。输入 1 s 进入单元格 100 和 101 L4 地图，以便为这些代码点亮。四个 0 填充剩余的 L4 单元格

L3 最初会亮起代码 ABC=011 .只要 L5 和 L4 亮起，它也会亮起。输入三个 1 s 进入单元格 011, 100, 101 对于 L3 地图。填三个0 s 进入剩余的 L3 单元。

ABC=010 的 L2 灯 和代码更大。填写1 s 进入单元格 010, 011, 100, 101 , 和两个 0 s 在剩余的单元格中。

L1 不亮的唯一时间是没有运动。已经有一个 0 在单元格 ABC=000 中 .所有其他五个单元格收到 1 s.

将 1 分组 's 如上所示，只要有较大的组结果，就使用 don't care。 L1图显示了三个乘积项，对应三组4细胞。

我们在两个组中都使用了不关心，在第三组中使用了一个不关心。无所谓让我们可以组成四人小组。

以类似的方式，L2 和 L4 映射都在不关心细胞的帮助下产生 4 细胞组。 L4 的减少是惊人的，因为 L4 灯由 A 到 D 转换器的最高有效位控制，L5=A .

灯 L4 不需要逻辑门。在 L3 和 L5 图中，单个单元格与不关心单元格形成两个一组。在所有五张地图中，简化的布尔方程都比没有不关心的复杂。

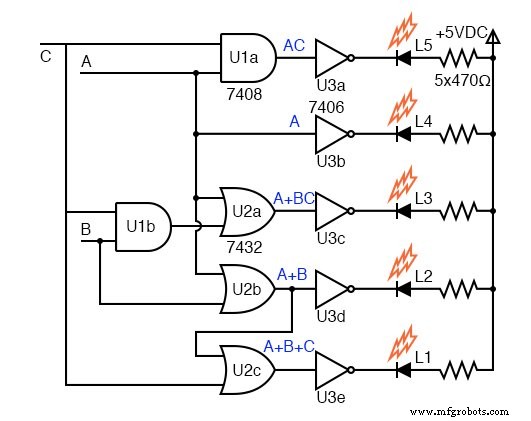
电路的门图如上所示。五个 K-map 方程的输出驱动逆变器。注意 L1 OR 门不是 3 输入门而是具有输入 (A+B), C 的 2 输入门 , 输出 A+B+C 开放收集器 逆变器，7406 , 可用于驱动 LED，但不是 K-map 逻辑设计的一部分。

集电极开路或逆变器的输出在集成电路封装内部的集电极处开路，因此所有集电极电流都可以流过外部负载。任何一个逆变器的高电平有效将输出拉低，通过 LED 和限流电阻吸收电流。

LED 很可能是为博物馆展览驱动 120 VAC 灯的固态继电器的一部分，此处未显示。

相关工作表：

• 数字显示电路工作表
• 卡诺图工作表