总和和产品符号
作为参考,本节介绍了一些文本中用于描述分配给卡诺图的 minterms 和 maxterms 的术语。否则,这里没有新材料。
Minterms 的术语
Σ (sigma) 表示总和,小写“m”表示最小项。 Σm 表示最小项的总和。重新审视以下示例以说明我们的观点。我们列出了最小项,而不是对未简化逻辑的布尔方程描述。
f(A,B,C,D) =Σ m(1, 2, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15) 或者 f(A,B,C,D) =Σ(m1,m2,m3,m4,m5,m7,m8,m9,m11,m12,m13,m15)
数字表示卡诺图中的单元格位置或地址,如下右图所示。这当然是一种描述 K-map 中最小项或单元格列表的紧凑方法。
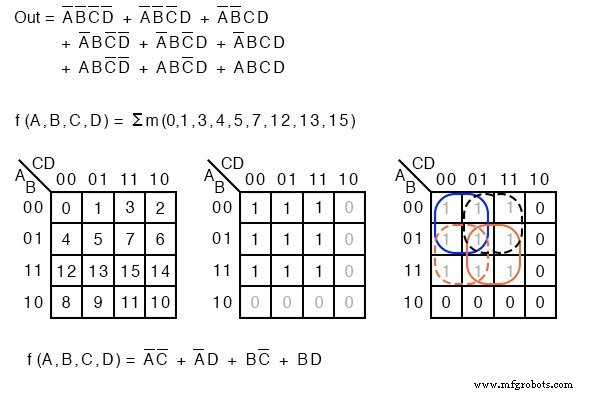
Sum-Of-Products 解决方案不受新术语的影响。最小项,1 s, 在地图中已经像往常一样分组并编写了 Sum-OF-Products 解决方案。
Maxterms 的术语
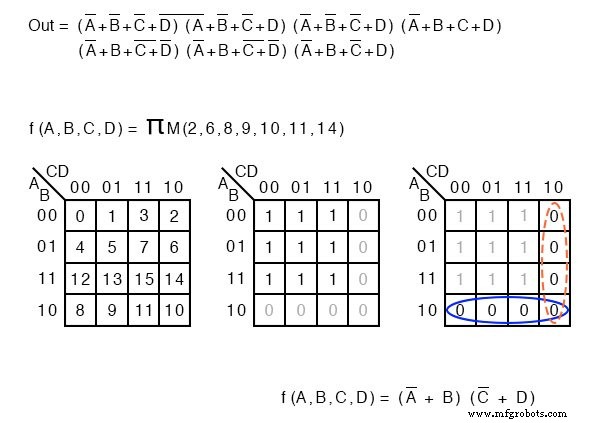
下面,我们展示了用于描述 maxterms 列表的术语。乘积由希腊语 Π (pi) 表示,大写“M”表示 maxterms。 ΠM 表示maxterms 的乘积。同样的例子说明了我们的观点。
未简化逻辑的布尔方程描述,由maxterms列表代替。
f(A,B,C,D) =Π M(2, 6, 8, 9, 10, 11, 14) 或者 f(A,B,C,D) =Π(M2, M6, M8, M9, M10, M11, M14)
再次,数字表示 K-map 单元格地址位置。对于 maxterms,这是 0 的位置 s,如下图。 Product-OF-Sums 解决方案以通常的方式完成。
$$Out =(A + B + \bar{C} + D)(A + \bar{B} + \bar{C} + D) + (\bar{A} + B + C + \bar{D }) + (\bar{A} + B + \bar{C} + D)$$
$$(\bar{A} + B + \bar{C} +\bar{D})(\bar{A} + \bar{B} + \bar{C} + D)$$
相关工作表:
- 乘积和乘积表达式工作表
- 卡诺图工作表
- 布尔代数工作表
工业技术


