更大的 5 和 6 变量卡诺图

较大的卡诺图减少了较大的逻辑设计。多大才够大？这取决于输入的数量，扇入 , 到正在考虑的逻辑电路。大型可编程逻辑公司之一给出了答案。

从其客户设计库中提取的 Altera 自己的数据支持异质性的价值。通过检查逻辑锥，将它们映射到基于 LUT 的节点并按照每个节点上最好的输入数量对它们进行排序，Altera 发现扇入的分布在 2 到 6 个输入之间几乎是平坦的，并且有一个很好的峰值五点钟。

对于大多数设计，答案是不超过六个输入，对于平均逻辑设计不超过五个输入。五变量卡诺图如下。

五变量K-map

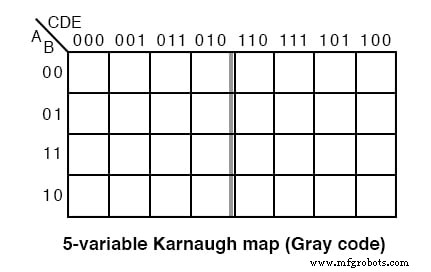
五变量 K-map 的旧版本，即格雷码图或反射图，如上所示。地图的顶部（以及 6 变量地图的侧面）以完整的格雷码编号。格雷码反映了代码的中间。此样式映射可在较旧的文本中找到。较新的首选样式如下。

K-map 的叠加版本

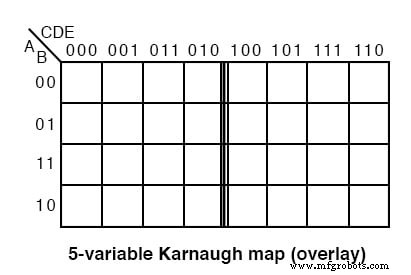
如上所示，卡诺图的覆盖版本只是两个（6 变量映射为四个）相同的图，除了顶部 3 位地址的最高有效位。

如果我们查看地图的顶部，我们会看到编号与之前的格雷码地图不同。如果我们忽略 3 位数字的最高有效位，序列 00, 01, 11, 10 位于叠加地图的两个子地图的标题处。八个三位数的序列不是格雷码。虽然最低有效两位中的四位的顺序是。

让我们使用我们的 5 变量卡诺图。设计一个具有 5 位二进制输入（A、B、C、D、E）的电路，其中 A 是 MSB（最高有效位）。它必须为输入数据中检测到的任何素数产生一个输出逻辑高。

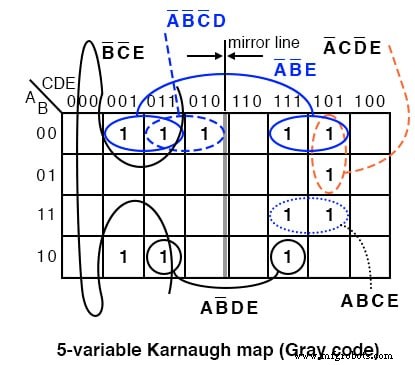
我们在较旧的格雷码（反射）图上展示了上述解决方案以供参考。质数是 (1,2,3,5,7,11,13,17,19,23,29,31)。绘制 1 在每个对应的单元格中。然后，继续对单元格进行分组。写出简化结果。

请注意，4 电池组 A'B'E 由镜像线两侧的两对电池组成。 2 细胞组 AB'DE 也是如此。通过在镜像线周围反射，它是一组 2 个单元格。使用这个版本的K-map时，在地图的另一半寻找镜像。

输出 =A'B'E + B'C'E + A'C'DE + A'CD'E + ABCE + AB'DE + A'B'C'D

下面我们展示的是更常见的5变量图，叠加图。

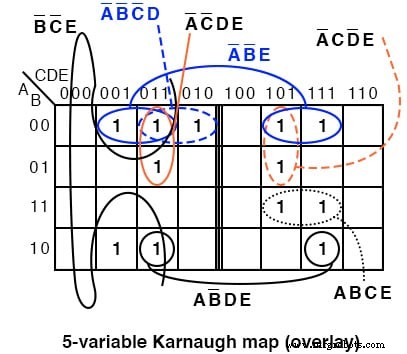
如果我们比较两个地图中的模式，地图右半部分的一些单元格会四处移动，因为地图顶部的寻址不同。我们还需要采用不同的方法来发现地图两半之间的共性。

将地图的一半覆盖在另一半之上。从上图到下图的任何重叠都是一个潜在的组。下图显示 AB'DE 组由两个堆叠的单元格组成。 A'B'E 组由两对堆叠的细胞组成。

对于 A'B'E 4 细胞组 ABCDE =00xx1 为组。即 A,B,E 是相同的 001 分别为组。而且，CD=xx 也就是说，它有所不同，CD=xx 没有共同点 对于 4 细胞组。由于 ABCDE =00xx1 , 4 个细胞组被 A'B'XXE =A'B'E 覆盖 .

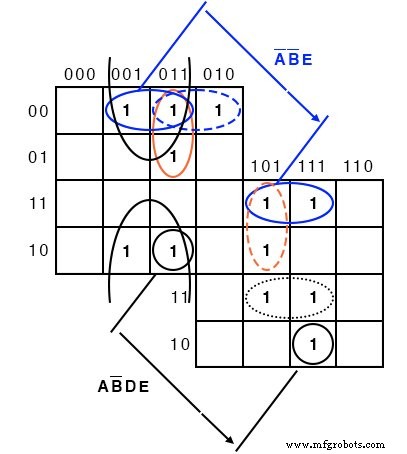
上面的 5 变量叠加图显示为堆叠式。

以下是六变量卡诺图的示例。我们在脑海中堆叠了四个子图以查看对应于 Out =C'F' 的 4 个单元格组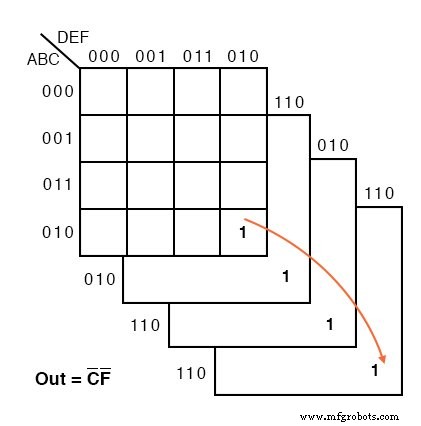

幅度比较器（用于说明 6 变量 K 映射）比较两个二进制数，指示它们在三个相应的输出上是否相等、大于或小于彼此。三位幅度比较器有两个输入 A2A1A0 和 B2B1B0 集成电路幅度比较器 (7485) 实际上有四个输入，但是，下面的卡诺图需要保持在合理的大小。我们只会解决A>B 输出。

6 变量 K-map

下面的 6 变量卡诺图有助于简化 3 位幅度比较器的逻辑。这是一种覆盖类型的地图。地图上下左右的二进制地址码不是完整的3位格雷码。

虽然四个子图的2位地址码是格雷码。通过将四个子地图相互堆叠来查找冗余表达式（如上所示）。可能存在所有四个地图共有的单元格，尽管在下面的示例中没有。它确实具有成对子图所共有的单元格。

上面的 A>B 输出是下面地图上的 ABC>XYZ。

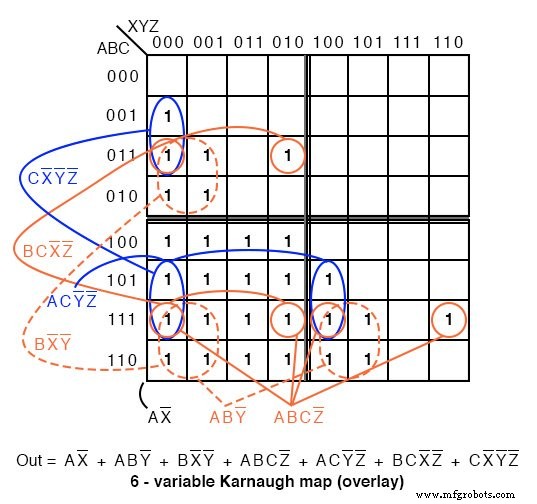
哪里有ABC 大于 XYZ , 1 被绘制。在第一行 ABC=000 不能大于 XYZ 的任何值 .没有1 s 在这一行。在第二行中，ABC=001 , 只有第一个单元格 ABCXYZ=001000 是 ABC 大于XYZ .单个 1 在第二行的第一个单元格中输入。第四行，ABC=010 , 有一对 1 s。第三行，ABC=011 有三个 1 s。因此，地图充满了 1 s 在 ABC 的任何单元格中 大于 XXZ .

在对单元格进行分组时，如果可能，请使用相邻的子图形成组。除了一组 16 个细胞外，所有细胞都涉及来自成对子图的细胞。查找以下组：

• 1 组 16 个细胞
• 2 组 8 细胞
• 4 组 4 细胞

16 细胞组，AX’ 占据所有右下子图；不过，我们没有在上图中圈出它。

一组 8 个单元格由上方子图中的一组 4 个单元格组成，覆盖左下方图中的相似组。第二组8个细胞由右侧子图中相似的4个细胞组覆盖在左下图中的同一组4个细胞上。

四组 4 单元格显示在上面的卡诺图上，并带有相关的乘积项。连同两组 8 个单元格和一组 16 个单元格的乘积项一起，显示了最终的乘积总和减少，所有七个项。

计算 1 s在地图中，一共有16+6+6=28个。在 K-map 逻辑归约之前，我们的 SOP 输出中有 28 个乘积项，每个都有 6 个输入。卡诺图产生了四个或更少输入的七个乘积项。这就是卡诺图的全部意义！

接线图未显示。但是，以下是使用 4 个 TTL 逻辑系列部件的 ABC>XYZ 的 3 位幅度比较器的部件清单：

• 1 ea 7410 三重 3 输入与非门 AX'、ABY'、BX'Y'
• 2 ea 7420 双 4 输入与非门 ABCZ'、ACY'Z'、BCX'Z'、CX'Y'Z'
• 1 ea 7430 8 输入与非门，用于输出 7-P 项

评论：

• 布尔代数、卡诺图和 CAD（计算机辅助设计）是逻辑简化的方法。逻辑简化的目标是成本最低的解决方案。
• 最低成本的解决方案是使用最少数量的门和最少的输入进行有效的逻辑简化。
• 维恩图使我们能够将布尔表达式可视化，从而轻松过渡到卡诺图。
• 卡诺图单元按格雷码顺序组织，以便我们可以将布尔表达式中的冗余可视化，从而简化。
• 更常见的 Sum-Of-Products (Sum of Minters) 表达式被实现为供给单个 OR 门 (sum) 的 AND 门（积）。
• Sum-Of-Products 表达式（AND-OR 逻辑）等效于 NAND-NAND 实现。所有与门和或门都被与非门取代。
• 很少使用，总和乘积表达式被实现为或门（总和）馈入单个与门（乘积）。 Product-Of-Sums 表达式基于 0 s，maxterms，在卡诺图中。