分支当前方法

第一种也是最直接的网络分析技术称为分支电流法 .在这种方法中，我们假设网络中的电流方向，然后通过基尔霍夫定律和欧姆定律编写描述它们相互关系的方程。一旦我们对每个未知电流有了一个方程，我们就可以求解联立方程并确定所有电流，从而确定网络中的所有电压降。

使用支流法求解

我们用这个电路来说明方法：

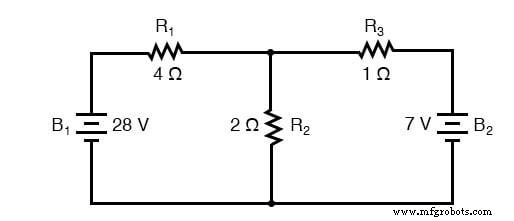
选择节点

第一步是在电路中选择一个节点（电线的结点）作为我们未知电流的参考点。我将选择连接 R1 右侧、R2 顶部和 R3 左侧的节点。

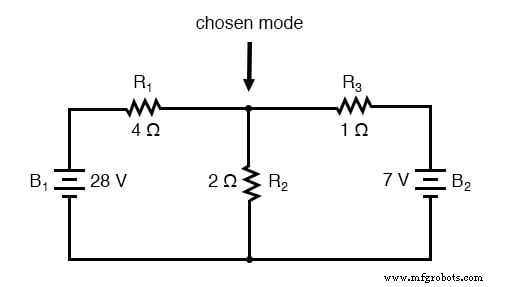
在该节点，猜测三根导线的电流流向，分别标记为 I1、I2 和 I3。请记住，这些电流方向此时是推测性的。幸运的是，如果事实证明我们的任何猜测是错误的，我们就会知道何时对电流进行数学求解（任何“错误”的电流方向都会在我们的解决方案中显示为负数）。

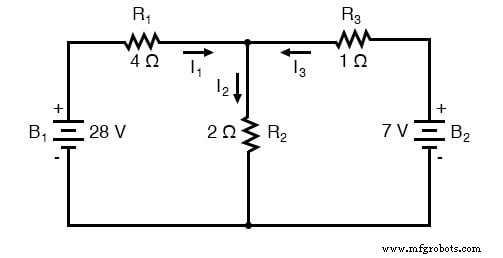
应用基尔霍夫电流定律 (KCL)

基尔霍夫电流定律 (KCL) 告诉我们进入和离开节点的电流的代数和必须为零，因此我们可以在一个方程中将这三个电流（I1、I2 和 I3）相互关联。为方便起见，我将表示任何当前进入 符号为正的节点，以及任何当前退出 符号为负的节点：

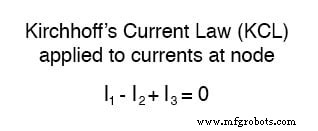
标记所有电压降

下一步是根据假定的电流方向标记电阻器上的所有电压降极性。电流进入电阻时极性为正，流出电阻时极性为负：

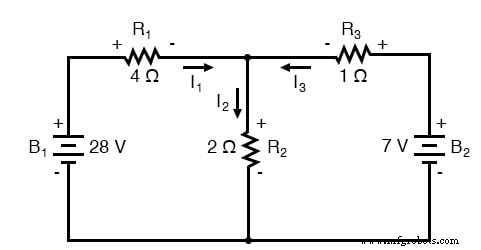
当然，电池极性根据其符号保持原样（短端负极，长端正极）。如果电阻压降的极性与最近的电池的极性不匹配，只要电阻电压极性基于通过它的假定电流方向是正确的。在某些情况下，我们可能会发现电流会被强制返回 通过电池，造成这种效果。这里要记住的重要一点是将所有电阻器极性和随后的计算都基于最初假设的电流方向。如前所述，如果您的假设碰巧不正确，那么一旦方程已经解出（通过负解）就会很明显。然而，解的大小仍然是正确的。

应用基尔霍夫电压定律 (KVL)

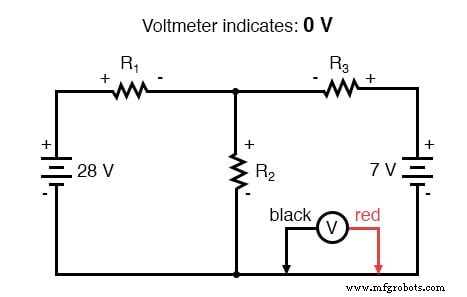
基尔霍夫电压定律 (KVL) 告诉我们，环路中所有电压的代数和必须为零，因此我们可以为联立方程创建更多包含电流项（I1、I2 和 I3）的方程。为了获得 KVL 方程，我们必须记录电路回路中的电压降，就像我们在用真正的电压表测量一样。我将选择首先跟踪该电路的左循环，从左上角开始逆时针移动（起点和方向的选择是任意的）。结果将如下所示：

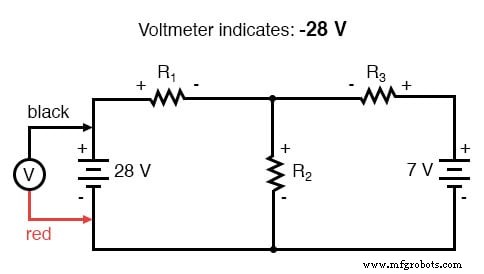
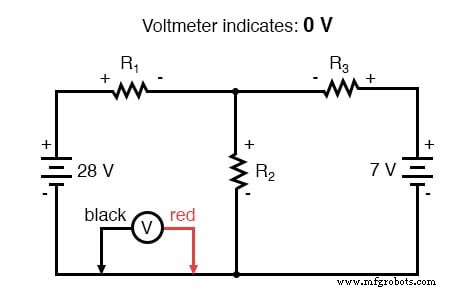
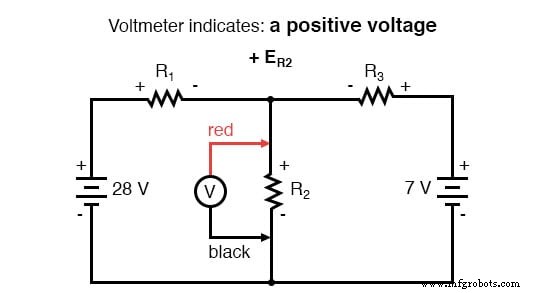
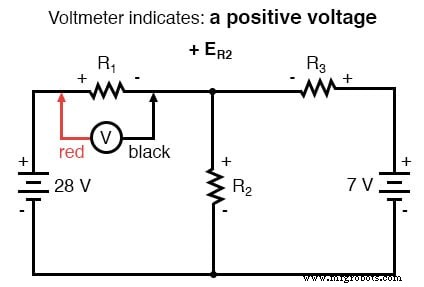
完成对左循环的跟踪后，我们将这些电压指示相加，得出的总和为零：

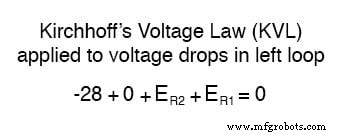
当然，我们还不知道 R1 或 R2 两端的电压是多少，因此此时我们无法将这些值作为数字插入到方程中。但是，我们做 知道所有三个电压必须以代数方式相加为零，所以等式是正确的。我们可以更进一步，将未知电压表示为相应的未知电流（I1 和 I2）与其各自电阻的乘积，遵循欧姆定律 (E=IR)，并消除 0 项：

由于我们知道所有电阻器的值是多少欧姆，我们可以将这些数字代入等式以简化一些事情：

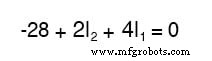
您可能想知道为什么我们要从其初始形式 (-28 + ER2 + ER1) 处理这个方程的所有麻烦。毕竟，最后两项仍然未知，那么将它们表示为未知电压或未知电流（乘以电阻）有什么好处？这样做的目的是得到使用相同未知变量表示的KVL方程 作为 KCL 方程，这是任何联立方程求解方法的必要条件。为了求解三个未知电流（I1、I2 和 I3），我们必须有三个与这三个电流相关的方程 （不是电压 !) 在一起。

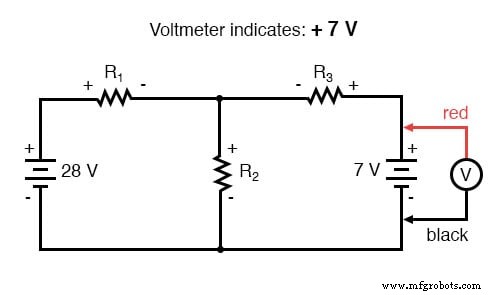
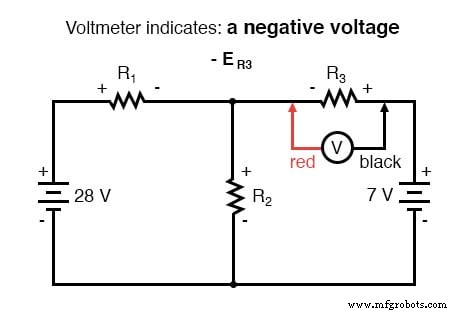
对电路的右侧循环应用相同的步骤（从所选节点开始逆时针移动），我们得到另一个 KVL 方程：

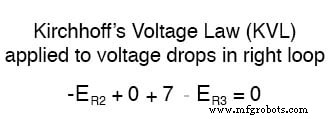
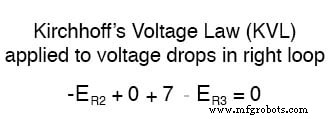
现在知道每个电阻器上的电压可以并且应该是 表示为相应电流和每个电阻的（已知）电阻的乘积，我们可以将等式改写为：

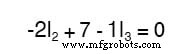
解决未知问题

现在我们有了一个由三个方程（一个 KCL 方程和两个 KVL 方程）和三个未知数组成的数学系统：

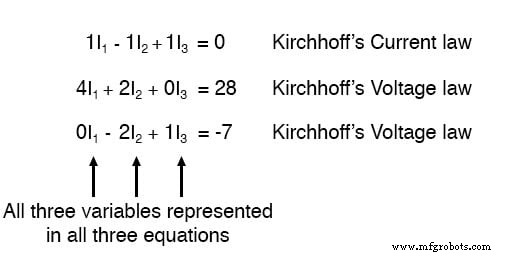
对于某些求解方法（尤其是任何涉及计算器的方法），将每个方程中的每个未知项、等号右侧的任何常数值以及任何“单位”项用显式系数表示是有帮助的1. 再次重写方程，我们有：

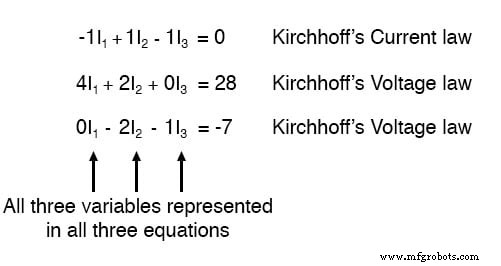
使用我们可用的任何解决方案技术，我们应该得出三个未知电流值的解决方案：

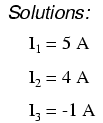
因此，I1 是 5 安培，I2 是 4 安培，而 I3 是负 1 安培。但“负”电流是什么意思？在这种情况下，这意味着我们的假设 I3 的方向与其真实相反 方向。回到我们原来的电路，我们可以重新绘制I3的电流箭头（并重新绘制R3压降的极性以匹配）：

重绘电路

请注意，由于电池 1 的电压较高（其电流像往常一样“向下”），电流是如何通过电池 2 向后推的（电子“向上流动”）！尽管电池 B2 的极性试图将电路的该分支中的电子向下推，但由于电池 B1 的优越电压，电子正被迫返回通过它。这是否意味着更强的电池总是“赢”而更弱的电池总是迫使电流反向通过它？不！它实际上取决于电池的相对电压和 电路中的电阻值。确定发生了什么的唯一可靠方法是花时间对网络进行数学分析。

计算所有电阻器的压降

现在我们知道了该电路中所有电流的大小，我们可以根据欧姆定律 (E=IR) 计算所有电阻器上的电压降：

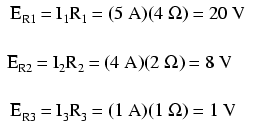
使用 SPICE 分析网络

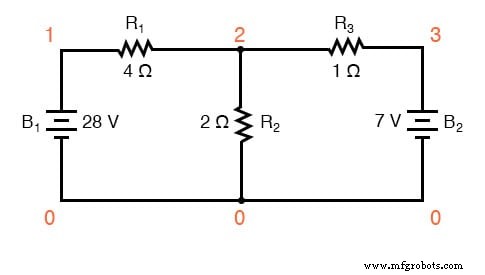
现在让我们使用 SPICE 分析这个网络来验证我们的电压数据。我们也可以使用 SPICE 分析电流，但由于这需要在电路中插入额外的元件，而且因为我们知道如果电压和电阻都相同，则电流 必须 em> 都是一样的，我会选择不太复杂的分析。这是我们电路的重新绘制，并附有节点编号供 SPICE 参考：

网络分析示例 v1 1 0 v2 3 0 直流 7 r1 1 2 4 r2 2 0 2 r3 2 3 1 .dc v1 28 28 1 .print dc v(1,2) v(2,0) v(2,3) 。结尾 v1 v(1,2) v(2) v(2,3) 2.800E+01 2.000E+01 8.000E+00 1.000E+00 

果然，电压值都相同：R1（节点 1 和 2）两端为 20 伏，R2（节点 2 和 0）两端为 8 伏，R3（节点 2 和 3）两端为 1 伏。请注意所有这些电压数字的符号：它们都是正值！ SPICE 根据节点列出的顺序确定其极性，第一个节点为正，第二个节点为负。例如，节点 1 和 2 之间的正 (+) 20 伏数字意味着节点 1 相对于节点 2 为正。如果在 SPICE 分析中该数字为负，我们就会知道我们的实际极性是“向后”（节点 1 相对于节点 2 为负）。查看SPICE列表中的节点顺序，我们可以看到极性都与我们通过分支电流分析方法确定的相符。

评论：

• “分支电流”分析方法要遵循的步骤：
  • 选择一个节点并假设电流方向。
  • 写出与节点电流相关的 KCL 方程。
  • 根据假定电流标记电阻器压降极性。
  • 为电路的每个回路写出 KVL 方程，用乘积 IR 代替方程的每个电阻项中的 E。
  • 求解未知分支电流（联立方程）。
  • 如果任何解为负，则该解的假定电流方向是错误的！
  • 求解所有电阻器上的压降 (E=IR)。

相关工作表：

• 直流支路电流分析工作表