诺顿定理。带示例的简单分步过程

直流电路分析中的诺顿定理

诺顿定理是另一种有用的电路分析技术，例如使用戴维南定理，它将线性、有源电路和复杂网络简化为简单的等效电路。 戴维南定理和诺顿定理的主要区别 也就是说，戴维南定理提供了一个等效的电压源和一个等效的串联电阻，而诺顿定理提供了一个等效的电流源和一个等效的并联电阻。

诺顿定理 声明：

换句话说，任何线性电路都等效于特定端子中的真实且独立的电流源。

相关文章：戴维宁定理。带有示例的简单分步过程（图片视图）

使用诺顿定理分析电路的步骤

短接负载电阻。
计算/测量短路电流。这是诺顿电流 (IN)。
开路电流源、短路电压源和开路负载电阻器。
计算/测量开路电阻。这是诺顿抵抗组织 (RN)。
现在，重新绘制电路，将步骤 (2) 中测量的短路电流 (IN) 作为电流源，将步骤 (4) 中测量的开路电阻 (RN) 作为并联电阻，并连接我们移除的负载电阻在步骤 (3) 中。这是必须简化和分析的线性电网或复杂电路的等效诺顿电路。你已经做到了。
现在使用分流器规则找到流过负载电阻的负载电流和负载电压。 IL =IN / (RN / (RN+ RL)) （（为了清楚的解释……查看下面给出的已解决示例）。

由解决的示例诺顿的定理：

示例：

利用诺顿定理求RN、IN、流过负载电阻的电流和负载电压（图1）。

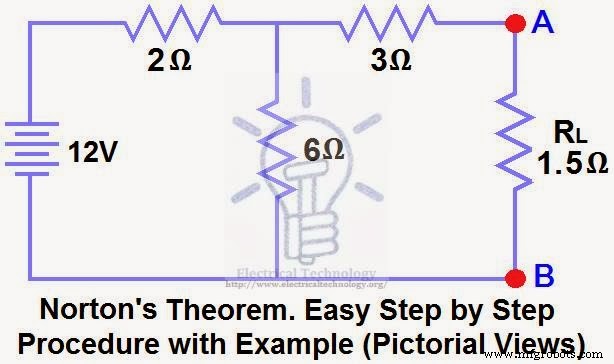
解决方法：-

第 1 步。

短接1.5Ω负载电阻，如图2所示。

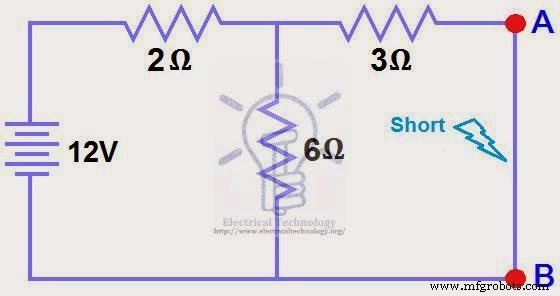
STEP 2.

计算/测量短路电流。这是诺顿电流 (IN)。

我们已将 AB 端子短接以确定诺顿电流 IN。然后 6Ω 和 3Ω 并联，然后 6Ω 和 3Ω 的这种并联组合与 2Ω 串联。

所以电路对Source的总电阻为：-

2Ω + (6Ω || 3Ω) ..... (|| =并行)。

RT =2Ω + [(3Ω x 6Ω) / (3Ω + 6Ω)] → IT =2Ω + 2Ω =4Ω。

RT =4Ω

IT =V ÷ RT

IT =12V ÷ 4Ω

IT =3A..

现在我们要找到 I_{SC =IN ... Apply CDR …（当前的分频器规则）…}

ISC =IN =3A x [(6Ω ÷ (3Ω + 6Ω)] =2A。

ISC =IN =2A.

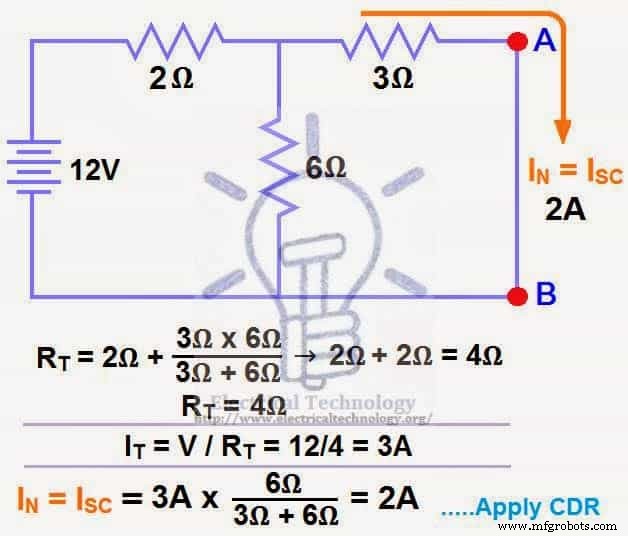
STEP 3.

开路电流源、短路电压源和开路负载电阻。图（4）

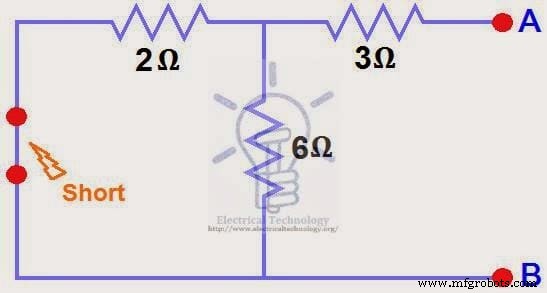
STEP 4.

计算/测量开路电阻。这是诺顿抵抗组织（RN）

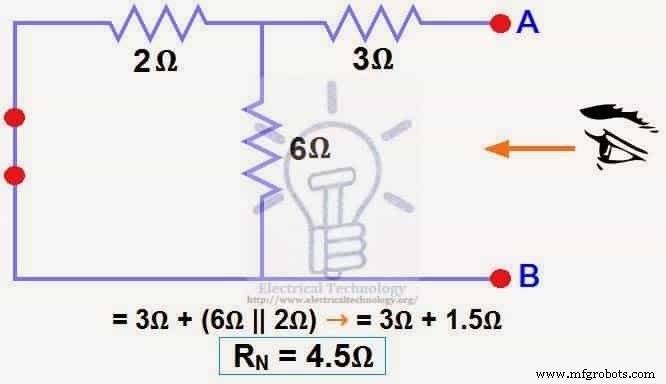
我们已经将12V直流电源降为零相当于在步骤（3）中用短路代替，如图（4）所示我们可以看到3Ω电阻为与 6Ω 电阻器和 2Ω 电阻器的并联组合串联。即：

3Ω + (6Ω || 2Ω) ..... (|| =平行)

RN =3Ω + [(6Ω x 2Ω) ÷ (6Ω + 2Ω)]

RN =3Ω + 1.5Ω

RN =4.5Ω

步骤 5.

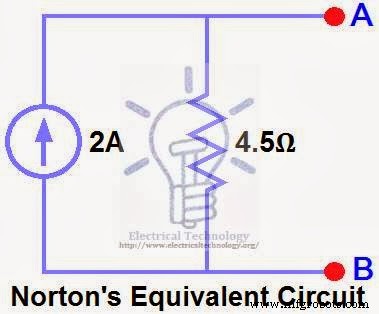
将 RN 与电流源 IN 并联并重新连接负载电阻。如图（6）所示，即带负载电阻的诺顿等效电路。

步骤 6.

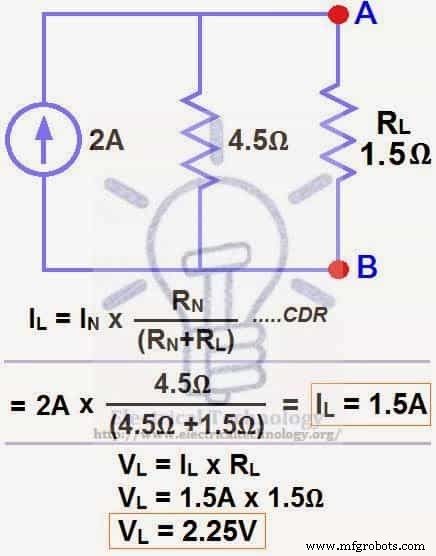
现在应用最后一步，即通过欧姆定律计算通过负载电阻的负载电流和负载电压，如图 7 所示。

负载电流通过负载电阻...

IL =IN x [RN ÷ (RN+ RL)]

=2A x (4.5Ω ÷ 4.5Ω + 1.5Ω) → =1.5A

IL =1. 5A

还有

负载电阻两端的负载电压...

VL =IL x RL

VL =1.5A x 1.5Ω

VL=2.25V

现在将这个简单的电路与给出的原始电路进行比较在图 1 中。您是否看到即使在更复杂的电路中，通过诺顿定理测量/计算不同负载电阻器的负载电流和负载电压会变得多么容易？只有也只有是的。

温馨提示： 诺顿和戴维南定理都可以应用于包含电阻、电感和电容器等差分元件的交流和直流电路。请记住，交流电路中的诺顿电流“IN”以复数（极性形式）表示，而，诺顿电阻“RN”以矩形表示。

诺顿定理。带示例的简单分步过程

直流电路分析中的诺顿定理

使用诺顿定理分析电路的步骤

由 解决的示例 诺顿的 定理：

由解决的示例诺顿的定理：