戴维南定理。带有已解决示例的分步过程

直流电路分析中的戴维南定理

一位法国工程师， M.L Thevenin ，在 1893 年实现了这些飞跃之一。戴维南定理 （也称为 亥姆霍兹-戴维南定理 ) 本身并不是一种分析工具，而是简化有源电路和复杂网络的一种非常有用的方法的基础。该定理有助于快速轻松地求解复杂的线性电路和网络，尤其是电路和电子网络。

戴维南定理 可以表述如下：

• VTH =戴维南电压
• RTH =戴维南的 阻力

相关文章：诺顿定理。带有示例的简单分步过程（图片视图）

使用戴维南定理分析电路的步骤

1. 打开负载电阻。
2. 计算/测量开路电压。这是戴维南电压 (VTH) .
3. 开路电流源和短电压源。
4. 计算/测量开路电阻。这是戴维南抵抗运动 (RTH) .
5. 现在，用测得的开路电压 (VTH) 重新绘制电路 在步骤 (2) 中作为电压源并测量 开路电阻 (RTH) 在步骤（4）中作为串联电阻并连接我们在步骤（1）中移除的负载电阻。这是等效戴维南电路 线性电网 或复杂的电路 必须通过戴维南定理进行简化和分析 .你已经做到了。
6. 现在使用欧姆定律求流经负载电阻的总电流：IT =VTH / (RTH + RL)。
   

相关文章：SUPERMESH 电路分析 |逐步解决示例

戴维宁定理求解示例：

示例：

查找 VTH、RTH 和负载电流 IL 在图 (1) 中流过负载电阻并在负载电阻上施加负载电压 使用戴维南定理 .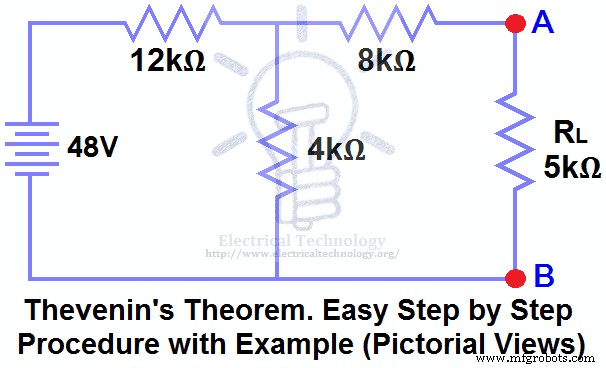

解决办法：-

步骤 1.

打开5kΩ负载电阻 （图 2）。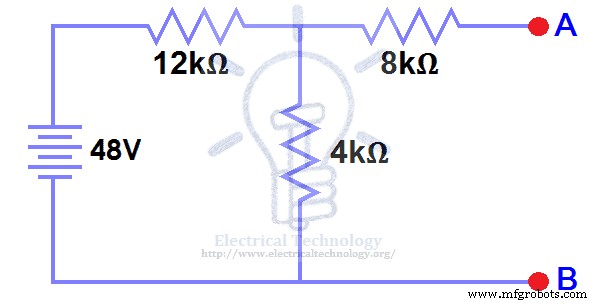

步骤 2.

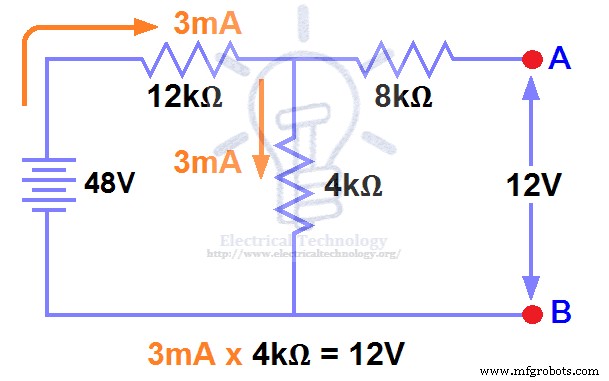
计算/测量开路电压。这是戴维南电压 (VTH) .图（3）。

我们已经去掉了图1中的负载电阻，所以电路变成了开路 如图 2 所示。现在我们必须计算戴维南电压。由于 3mA 电流在两个 12kΩ 中流动 4kΩ 电阻 因为这是一个串联电路，电流不会在 8kΩ 中流动 电阻打开。

这样，12V (3mA x 4kΩ) 将出现在 4kΩ 电阻 .我们也知道电流不会流过 8kΩ 电阻，因为它是开路的，但 8kΩ 电阻与 4k 电阻 并联 .所以相同的电压，即 12V 将出现在 8kΩ 电阻上 以及4kΩ电阻。因此 12V 将出现在 AB 端子上。即，

VTH =12V

步骤 3.

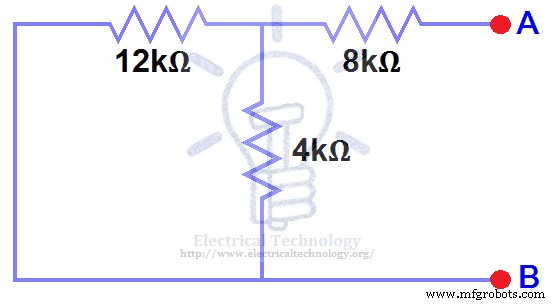
打开当前资源 和短电压源 如下所示。图（4）

步骤 4.

计算/测量开路电阻 .这是戴维宁抵抗运动（RTH）

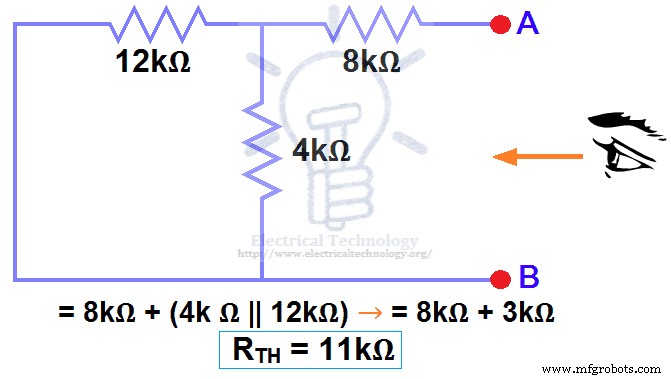
我们已移除 48V 直流电源 到零 作为等效，即 48V 直流电源已在步骤 3 中用短路代替（如图 3 所示）。我们可以看到 8kΩ 电阻与 4kΩ 电阻和 12k Ω 电阻串联。即：

8kΩ + (4k Ω || 12kΩ) ..... (|| =并联)

RTH =8kΩ +  [(4kΩ x 12kΩ) / (4kΩ + 12kΩ)]

RTH =8kΩ + 3kΩ

RTH =11kΩ

步骤 5.

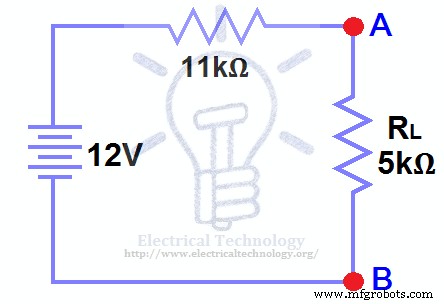
将RTH与电压源VTH串联，重新连接负载电阻。这如图（6）所示，即带负载电阻的戴维宁电路。这是戴维南等效电路 .

步骤 6.

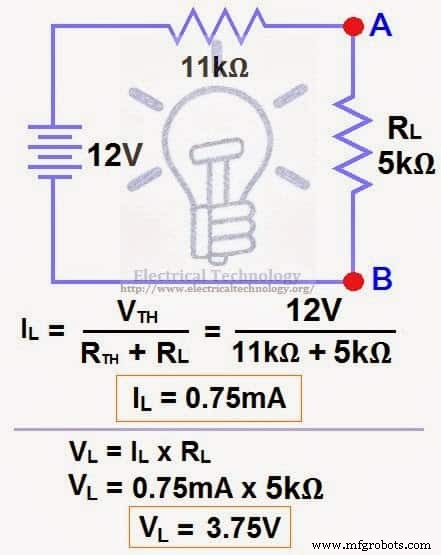
现在应用最后一步，即欧姆定律。 计算总负载电流和负载电压 如图6所示。

IL =VTH / (RTH + RL)

IL =12V / (11kΩ + 5kΩ) → =12/16kΩ

IL =0.75mA

和

VL =IL x RL

VL =0.75mA x 5kΩ

VL=3.75V

现在将这个简单的电路与图1所示的原始电路进行比较。您是否看到在复杂的电路和网络中测量和计算不同的负载电流会容易得多戴维南定理的负载电阻 ?是的，只有是的。

很高兴知道： 戴维南定理和诺顿定理都可以应用于包含差分元件（如电阻器、电感器和电容器等）的交流和直流电路。请记住，交流电路中的戴维南电压“VTH”以复数（极性形式）表示，而，戴维南电阻“RTH”以矩形表示。

相关帖子：

• 交流和直流电路的最大功率传输定理
• 基尔霍夫电流和电压定律 (KCL &KVL) |解决的例子
• 补偿定理 - 证明、解释和求解示例
• 替换定理 - 带求解示例的分步指南
• 米尔曼定理 - 分析交流和直流电路 - 示例
• 叠加定理 - 带求解示例的电路分析
• Tellegen 定理 - 求解示例和 MATLAB 仿真
• SUPERNODE 电路分析 |逐步解决示例
• SUPERMESH 电路分析 |逐步解决示例
• 分压器规则 (VDR) - R、L 和 C 电路的求解示例
• 分流器规则 (CDR) - 交流和直流电路的求解示例
• Star 到 Delta 和 Delta 到 Star 的转换。 Y-Δ 变换