诺顿定理
什么是诺顿定理?
诺顿定理指出,可以将任何线性电路(无论多么复杂)简化为仅具有单个电流源和连接到负载的并联电阻的等效电路。正如戴维南定理一样,“线性”的限定与叠加定理中的限定相同:所有潜在方程都必须是线性的(没有指数或根)。
简化线性电路
将我们的原始示例电路与 Norton 等效电路进行对比:它看起来像这样:
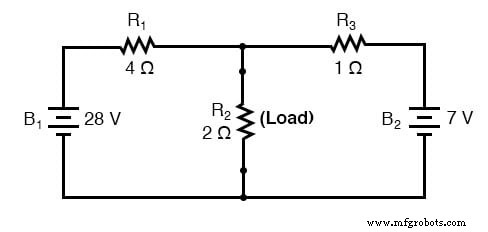
. . .诺顿转换后。 . .
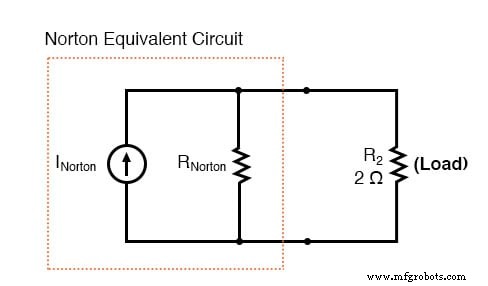
请记住,当前来源 是一个组件,其工作是提供恒定量的电流,输出尽可能多或尽可能少的电压以维持该恒定电流。
戴维宁定理与诺顿定理
与戴维南定理一样,原始电路中除负载电阻外的所有内容都已简化为更易于分析的等效电路。与戴维南定理类似的还有诺顿定理中计算诺顿源电流(INorton)和诺顿电阻(RNorton)的步骤。
确定负载电阻
和以前一样,第一步是识别负载电阻并将其从原始电路中移除:
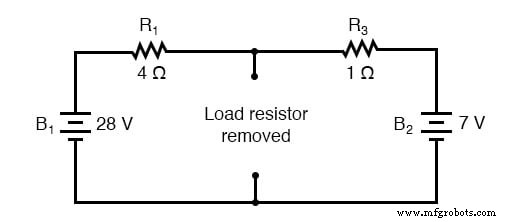
查找诺顿电流
然后,要找到诺顿电流(用于诺顿等效电路中的电流源),请在负载点之间放置直接导线(短路)连接并确定合成电流。请注意,此步骤与戴维南定理中的相应步骤完全相反,我们将负载电阻替换为断路(开路):
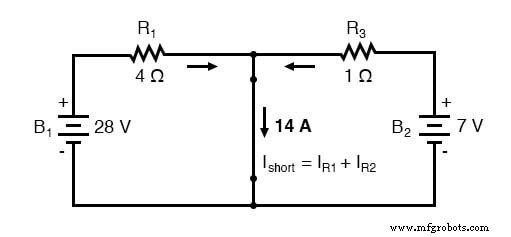
当负载电阻连接点之间的电压降为零时,通过 R1 的电流严格取决于 B1 的电压和 R1 的电阻:7 安培 (I=E/R)。同样,通过 R3 的电流现在严格地是 B2 的电压和 R3 的电阻的函数:7 安培 (I=E/R)。通过负载连接点之间短路的总电流是这两个电流的总和:7 安培 + 7 安培 =14 安培。这个 14 安培的数字成为我们等效电路中的诺顿源电流 (INorton):
找到诺顿阻力
请记住,电流源的箭头符号指向常规电流的方向。 为了计算诺顿电阻 (RNorton),我们执行与计算戴维宁电阻 (RThevenin) 完全相同的操作:采用原始电路(负载电阻仍被移除),移除电源(与我们采用相同的方式)使用叠加定理:电压源用电线代替,电流源用断路代替),并计算从一个负载连接点到另一个负载连接点的总电阻:
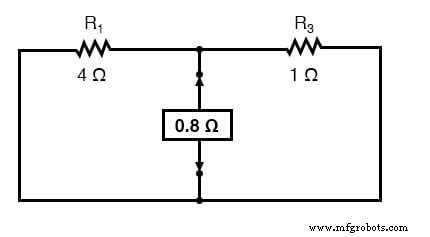
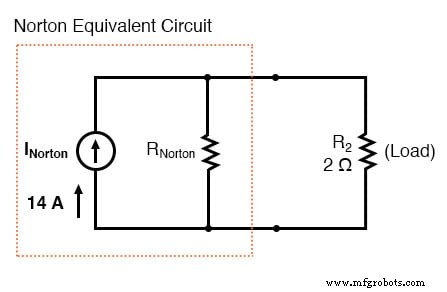
现在我们的诺顿等效电路如下所示:
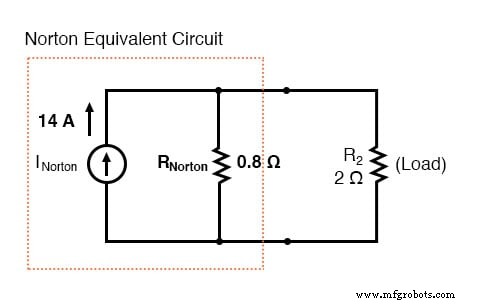
确定负载电阻两端的电压
如果我们重新连接我们原来的 2 Ω 负载电阻,我们可以将诺顿电路分析为一个简单的并联排列:
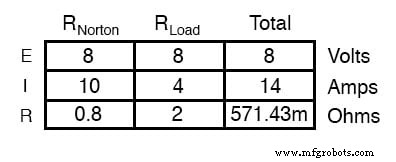
与戴维南等效电路一样,此分析中唯一有用的信息是 R2 的电压和电流值;其余信息与原始电路无关。然而,戴维宁定理的相同优点也适用于诺顿定理:如果我们希望在几个不同的负载电阻值上分析负载电阻器电压和电流,我们可以一次又一次地使用诺顿等效电路,只应用比简单的并行电路分析,以确定每个试验负载发生的情况。
评论:
- 诺顿定理是一种将网络简化为由单个电流源、并联电阻和并联负载组成的等效电路的方法。
- 诺顿定理的步骤:
- 通过从原始电路中移除负载电阻器并计算穿过负载电阻器曾经所在的开路连接点的短路(电线)的电流,找到诺顿源电流。
- 通过移除原始电路中的所有电源(电压源短路和电流源开路)并计算开路连接点之间的总电阻,找出诺顿电阻。
- 绘制诺顿等效电路,其中诺顿电流源与诺顿电阻并联。负载电阻重新连接在等效电路的两个开路点之间。
- 按照并联电路的规则分析负载电阻的电压和电流。
相关工作表:
- 戴维南、诺顿和最大功率传输定理工作表
工业技术


