单分子磁隧道结中的可控自旋切换

摘要

提出了一种新型自旋电流滤波器，它由耦合到两个普通金属电极的单分子磁体 (SMM) 组成。结果表明，该隧道结可以产生高度自旋极化的电流，其自旋极化可以通过施加到 SMM 的磁场和栅极电压来切换。 SMM 隧道结中的这种自旋转换是由通过 SMM 最低未占据分子轨道的自旋选择性单电子共振隧穿引起的。在没有外加磁场的情况下，电子电流谱仍然是自旋极化的，这有助于判断分子的自旋态是否达到了基态双峰$|\pm S\rangle$。该器件可以用现有技术实现，可能在自旋电子学和量子信息方面具有实际应用。

介绍

近年来，随着材料科学的发展，纳米分子电子器件在纳米器件和自旋电子学中的潜在应用得到了广泛的研究[1,2,3]。由于它们的小尺寸和低功耗，许多利用分子的基本设备已经被证明，包括具有负差分电阻的隧道结 [4]、整流器 [5]、放大器 [6] 和数据存储 [7]。与传统的半导体器件不同，由单个分子组成的分子器件似乎非常适合用作可控分子开关 [8]。尽管已经在原子量子点接触中报道了分子尺度切换 [9,10,11]，但单分子结提供了额外的灵活性，能够通过分子设计调整开/关电导状态。在过去几十年成功测量流过单个分子的电流之后，已经报道了各种分子开关，如光控分子开关 [12] 和机械控制单分子开关 [13]，可用于在高和低电导状态之间转换设备。然而，所有这些切换方案都只能调节电荷传输电导，而不是依赖于自旋的传输特性。

近年来，一种被称为单分子磁体 (SMM) 的新型分子材料已被证明是作为基于分子的自旋电子器件的基本组件的合适候选材料 [14]。与其他分子相比，SMM 是具有相对较大的净自旋矩（对应于自旋数 S ) 和显着的单轴磁各向异性 [15]。在低温下，SMM 将陷入两种亚稳态自旋状态 $|\pm S\rangle$ [16] 之一。这种双稳态使 SMM 成为存储单元的合适基础 [17, 18]，并激发了许多研究 SMM 其他物理特性的努力。到目前为止，已经通过实验研究了 SMM 和普通金属 [19,20,21] 或超导体 [22] 界面之间的电子跃迁，以及通过磁场和电向 SMM 写入和读取信息的功能。在$\hbox {TbPc}_{{2}}$ 分子中也证明了偏置[23]。受这些工作的启发，预计 SMM 中隧道电流的自旋极化也可以通过磁场和栅极电压进行切换；然而，目前还没有提出基于这种SMM隧道结的可控开关方案。

方法

在这封信中，我们展示了 SMM 隧道结中的一种新型自旋切换效应，可用于通过改变施加于分子的外部磁场在纯自旋向上和自旋向下电子电流之间切换。如图 1a 所示，该纳米结构由连接到两个普通金属电极的 SMM 组成。 SMM 的能级由栅极电压调节，SMM 的自旋磁化可以通过外部磁场切换。从图 1b 中，我们可以看到该器件中的磁场控制自旋注入需要两步方案：首先，它应用相对较大的外部磁场来“写入”SMM 的自旋方向。根据磁场的方向，SMM 的核心自旋将切换到两个亚稳态自旋状态 $\pm \,S$ 之一。自旋注入过程包括在没有磁场的情况下使用施加在两条引线上的电偏置。由于两条引线的化学势不同以及SMM的磁各向异性，只有自旋平行于SMM磁化的电子才能流过结[14]，使电流高度极化。系统的总哈密顿量写为 [24, 25]

$$\begin{aligned} H&=\varepsilon _{0}\sum _{\sigma }c_{\sigma }^{\dag }c_{\sigma }+Uc_{\uparrow }^{\dag }c_{ \uparrow }c_{\downarrow }^{\dag }c_{\downarrow } -{\mathcal {D}}(S^{z})^{2}-J {\mathbf {s}}\cdot {\ mathbf {S}} \nonumber \\&\quad -\Delta B(s^{z}+S^{z})+\sum _{k,\sigma ,\alpha }(t_{\alpha }a_{ \alpha k\sigma }^{\dag }c_{\sigma }+t^{*}_{\alpha }c^{\dag }_{\sigma }a_{\alpha k\sigma }) \nonumber \ \&\quad +\sum _{k,\sigma ,\alpha }\varepsilon _{k\sigma }a_{\alpha k\sigma }^{\dag }a_{\alpha k\sigma }。 \end{对齐}$$ (1)

这里，$\varepsilon _{0}$ 是 SMM 的最低未占分子轨道 (LUMO) 的现场能量，可以通过施加到 SMM 的栅极电压来移动； $c_{\sigma }^{\dag }$ ($c_{\sigma }$) 是电子产生（湮灭）算子，$\sigma$ 作为泡利自旋指数； U 表示库仑排斥能； ${\mathcal {D}}$ 是磁单轴各向异性参数。 J 是导电电子自旋之间的交换相互作用，${\mathbf {s}} =\sum \nolimits _{\sigma \sigma ^{\prime }}c_{\sigma }^{\dag }\sigma _{\sigma \sigma ^{\prime }}c_{\sigma ^{\prime }}/2$，在LUMO能级和局部自旋${\mathbf {S}}$。由于我们假设分子的易轴是自旋空间中的 z 轴，$\Delta B(s^{z}+S^{z})$ 描述了与施加的磁场相关的塞曼分裂沿着这个简单的轴，g 因子和玻尔磁子 $\mu _{B}$ 被吸收到 $\Delta B$ 中。 $a_{\alpha k\sigma }^{\dag }$ ($a_{\alpha k\sigma }$) 是动量 k 电子的创造（湮灭）算子、自旋 $\sigma$ 和能量 $\varepsilon _{k\sigma }$ 在铅 $\alpha$ 中。 SMM 和普通金属引线之间的隧道耦合强度，用 $t_{\alpha }$ 表示，与动量 k 无关并旋转$\sigma$.

很容易对孤立的 SMM 的哈密顿量 $H_{{\mathrm{mol}}}$ 进行对角化，即方程中的前五项。 (1).如果我们定义 ${\mathbf {S}}_{T}={\mathbf {s}}+{\mathbf {S}}$，可以证明特征值 m 由于交换关系 $[S_{T}^{z},H_{{\mathrm{mol}}}]=0$，$S_{T}^{z}$ 是一个很好的量子数.在以下表达式中，$|\bullet \rangle _{L({\mathrm{mol}})}$ 表示 LUMO (SMM) 的自旋状态。将 $n=0,1,2$ 定义为 LUMO 中的电子数，特征能可以通过以下方式获得 [26]： $\varepsilon _{|0,m\rangle }=-{\ mathcal {D}}m^{2}-\Delta Bm$ 对于本征态 $|0,m\rangle =|0\rangle _{L}\otimes |m\rangle _{{\mathrm{mol} }}$, $\varepsilon _{|1,m\rangle ^{\pm }}=\varepsilon _0 -\Delta B m+J/4-{\mathcal {D}}(m^{2} +1/4)\pm \Delta \varepsilon (m)$ 对于本征态 $|1,m\rangle ^{\pm }=C_{1}^{\pm }|\downarrow \rangle _{L }\otimes |m+1/2\rangle _{{\mathrm{mol}}}+C_{2}^{\pm }|\uparrow \rangle _{L}\otimes |m-1/2\rangle _{{\mathrm{mol}}}$ 和 $\varepsilon _{|2,m\rangle }=2\varepsilon _0 +U-{\mathcal {D}}m^{2}-\Delta B m$ 用于本征态 $|2,m\rangle =|\uparrow \downarrow \rangle _{L}\otimes |m\rangle _{{\mathrm{mol}}}$。这里，$\Delta \varepsilon (m)=\sqrt{{\mathcal {D}}({\mathcal {D}}-J)m^{2}+(J/4)^{2}(2S +1)^{2}}$ 和 $C_{1}^{\pm }$ 和 $C_{2}^{\pm }$，在参考文献中给出。 [24]，作为有效的 Clebsch-Gordan 系数。

传输过程由通过 SMM 级别的顺序隧道控制，而弱联合隧道和直接隧道可以安全地忽略。对于 SMM 和引线之间的弱耦合，主方程方法成立。流过 SMM 的总自旋-$\sigma$ 电流可以写成 $I_{\sigma }=(I_{L\sigma }-I_{R\sigma })/2$，其中 $ I_{L\sigma }$ ($I_{R\sigma }$) 代表自旋-$\sigma$ 电流从左（右）引线流向 SMM，屈服

$$\begin{aligned} I_{\alpha \sigma }=-(e/h)\sum _{i,f}(n_{i}-n_{f})R_{\alpha \sigma }^{f \rightarrow i}P_{f}, \end{aligned}$$ (2)

使得总电流等于 $I=\sum _{\sigma }(I_{L\sigma }-I_{R\sigma })/2$ 并且电流的自旋极化系数为 $\ eta =\frac{ I_{\alpha \uparrow } - I_{\alpha \downarrow }}{ I_{\alpha }} \times 100\%$。在方程式中。 (2)、$R_{\alpha \sigma }^{f\rightarrow i}$表示状态$|i\rangle$和$|f\rangle$之间的转换率，表示为$ R_{\alpha \sigma }^{f\rightarrow i}=\Gamma _{\alpha \sigma }[f(\varepsilon _{i}-\varepsilon _{f}-\mu _{\alpha })\ langle i|c_{\sigma }^{\dag }|f\rangle ^{2}+f(\varepsilon _{i}-\varepsilon _{f}+\mu _{\alpha })\langle f| c_{\sigma }^{\dag }|i\rangle ^{2}]$，其中 $\Gamma _{\alpha \sigma }=2\pi D_{\alpha \sigma }|t_{\alpha }|^{2}$ 是铅$\alpha$ 的线宽函数，$D_{\alpha \sigma }$ 是$E_{F}$ 处的态密度，而$f_{\alpha }$ 是铅$\alpha$ 在温度$T_{\alpha }$ 和化学势$\mu _{\alpha }$ 下的费米函数。 $P_{i}$ 表示在状态 $|i\rangle$ 中找到 SMM 的概率。遵循 Timm [26] 和 Shen [27] 建议的数值方法，概率 $P_{i(t)}$ 和稳态概率 $P_{i(t\rightarrow \infty )}$ 可以通过求解一组速率方程得到 ${\mathrm{d}}P_{i}/{\mathrm{d}}t=\sum _{f}R_{i,f}P_ {i}$.

这里，对$\hbox {Mn}_{{12}}$-Ac 分子隧道结[19, 28] 进行数值计算，自旋数为$S=10$，${\mathcal { D}}=0.06$ meV、$J=0.1$ meV 和 $U=25$ meV。所考虑的电极由普通金属制成，因此线宽函数与自旋无关，即为简单起见，$\Gamma _{\alpha \sigma }=\Gamma _{0}$。

<图片>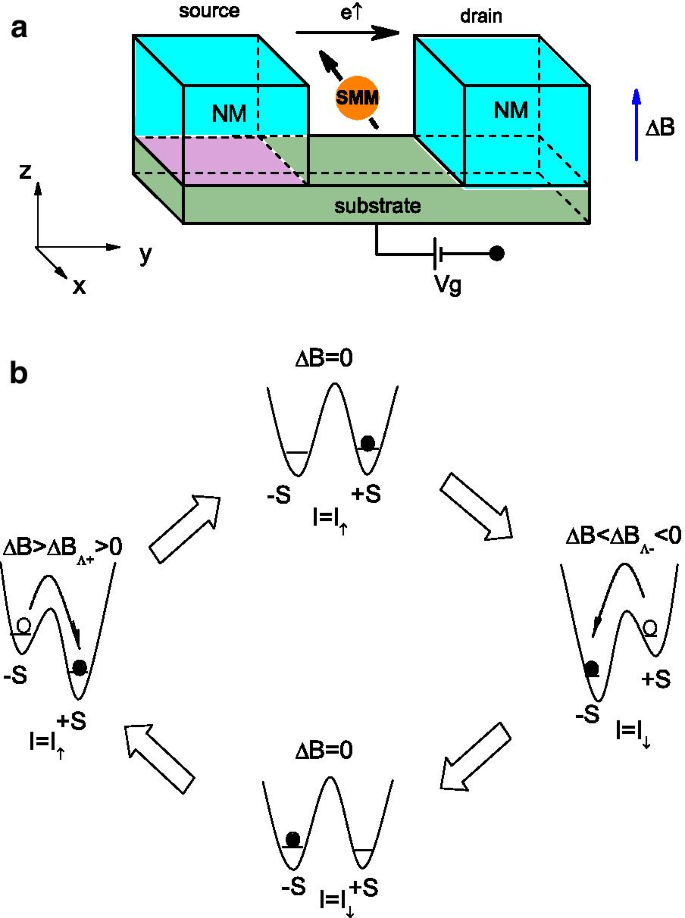

一自旋滤波器或自旋存储器的示意图，由耦合到一对非磁性电极的 SMM 组成。 b 外磁场作用下SMM磁化和隧道电流自旋极化的切换示意图

<图片>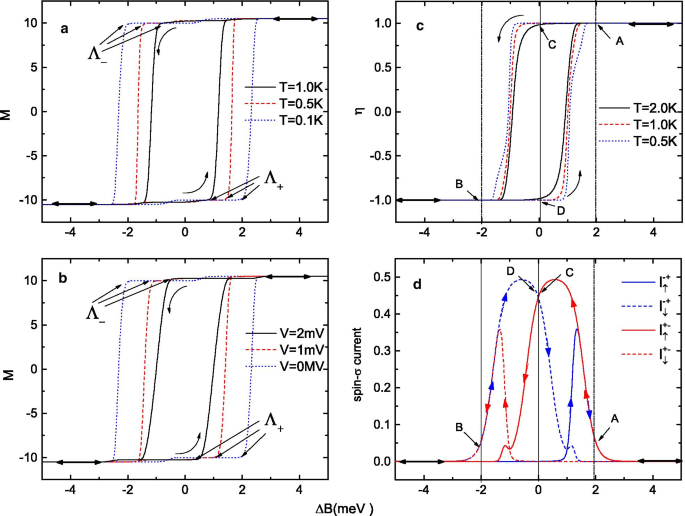

一 , b a 的 SMM 磁滞回线不同的平衡温度和b 外磁场$\Delta B$ 来回扫描时的不同偏置电压。 c 不同平衡温度和d下隧道电流的自旋极化当外部磁场 $\Delta B$ 被扫描回时，$T=0.5$ K 处的自旋-$\sigma$ 电流（按 $e\Gamma_{0} /\hbar$ 缩放）在 $V=1$ mV

的固定偏置下来回 <图片>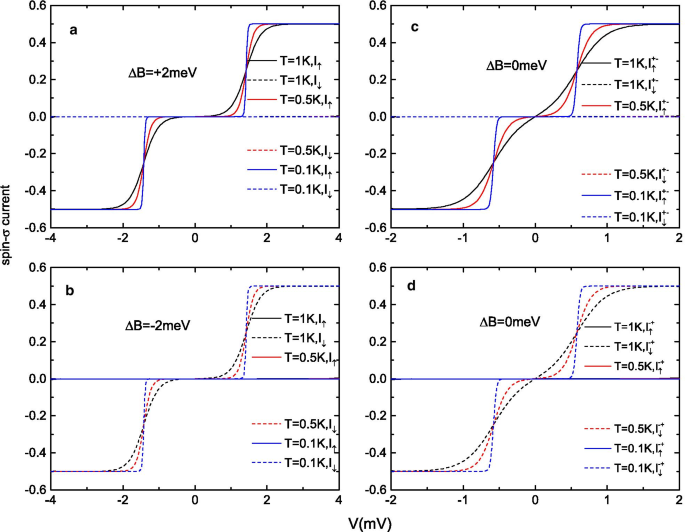

自旋-$\sigma$ 电流$I_{\uparrow (\downarrow )}$（按$e\Gamma_{0} /\hbar$ 缩放）(a , b ) 在 a 的外部磁场存在下 $\Delta B=+2$ meV, b $\Delta B=-\,2$ meV, c , d 在没有磁场时作为偏置电压的函数

<图片>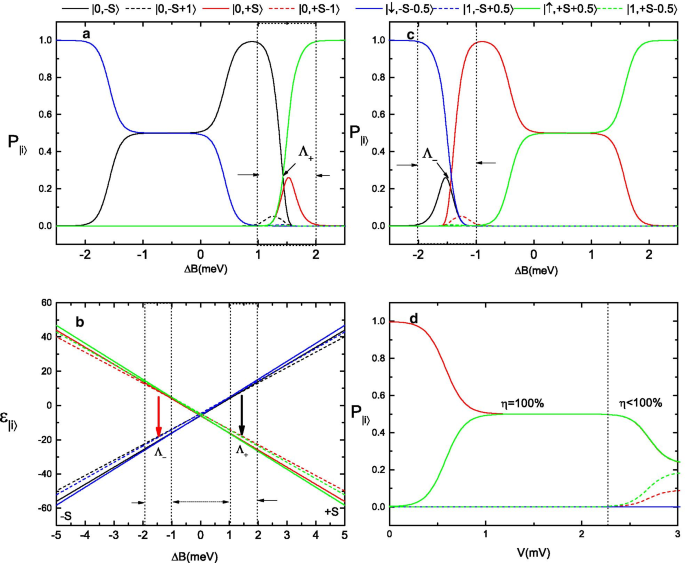

一 , c 分子态概率的变化 a 因为 $\Delta B$ 从 ${-}\,5$ meV 扫描到 ${+}\,5$ meV 和 c 因为 $\Delta B$ 从 $+\,5$ meV 扫描到 ${-}\,5$ meV。 b 当 $\Delta B$ 从 ${-}$ 5 meV 变为 ${+}$ 5 meV 时，这些自旋状态的塞曼图。 d 当分子的自旋状态最初准备为 $P_{|0,+S\rangle }=1$ 和 $P_{i}=0$<时，分子状态概率的变化作为偏置电压的函数/P> <图片>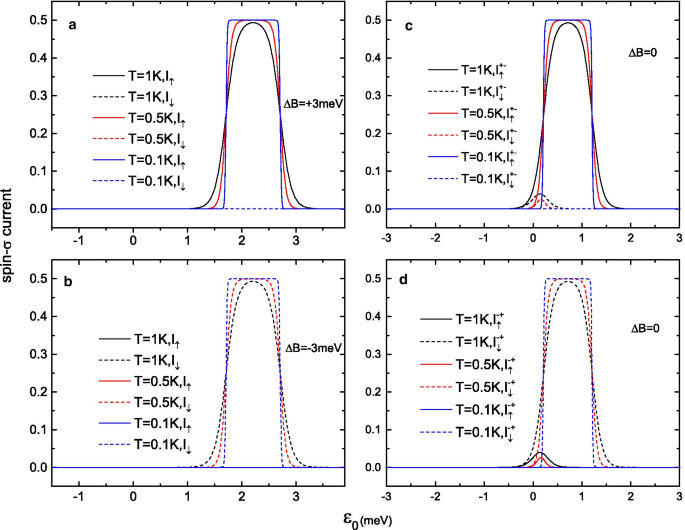

自旋-$\sigma$ 电流$I_{\uparrow (\downarrow )}$ a , b 在 a 的外部磁场存在下 $B=+2$ meV 或 b $B=-\,2$ meV 和 c , d 在没有磁场的情况下作为分子水平的函数 $\varepsilon _{0}$

结果与讨论

首先，我们演示了如何使用磁场 $\Delta B$ 来“写入”SMM 的自旋态。在图 2 中，我们绘制了 SMM 的磁化强度、电流的自旋极化 $\eta$ 和作为 $\Delta B$ 函数的自旋-$\sigma$ 电流，带有偏置施加在结上的电压。箭头表示磁场的扫描方向，并且假定扫描过程足够慢以允许系统弛豫到稳定状态。在图 2a-c 中，表明当磁场 $\Delta B$ 来回扫描时，分子的磁化强度和电流的自旋极化都表现出环形结构。为便于描述，我们用$\Lambda _{-}$ 来表示SMM 的磁化强度从$+S\rightarrow -S$ 和$\Lambda _{+}\ ) 表示 \(-S\rightarrow +S$ 的反转点。在图 2a、b 中，针对不同的平衡温度和偏置电压，SMM 的磁化强度被绘制为 $\Delta B$ 的函数。很明显，热波动和电偏压都能够在 $\Delta B$ 恰好达到激活能之前激活磁反转。因此，磁滞回线随着平衡温度或偏置电压的增加而缩小，$\Lambda _{+}$ 和$\Lambda _{-}$ 之间的距离减小。然而，无论磁滞回线缩小多少，隧道电流的自旋极化系数总是可以达到极高的值 $\eta =\pm 100\%$ 除非 $\Delta B$ 接近两个反转点，$\Lambda _{+}$ 和 $\Lambda _{-}$。进一步发现小磁场区域电流自旋极化$\Delta B_{\Lambda _{-}}<\Delta B<\Delta B_{\Lambda _{+}}\ ) 与大磁场区域 \(\Delta B<<\Delta B_{\Lambda _{-}}$ 或 $\Delta B>>\Delta B_{\Lambda _{ +}}$。如图 2c 所示，在大磁场范围内，隧道电流的自旋极化系数 $\eta$ 可以概括为

<图片>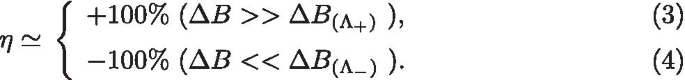

在这种情况下，例如，在图 2c、d 中的 A 点（B 点），给定的外部磁场 $\Delta B$ 对应于分子的单个确定性磁化强度，并且只有 $100 \%$ 自旋向上（spin-down）的电子电流可以流过结。然而，在低磁场区域 $\Delta B_{\Lambda _{-}}<\Delta B<\Delta B_{\Lambda _{+}}$，SMM 的原始磁化强度可以保持不变，$+S$ 和$-S$ 自旋方向都可以保留。在图 2d 中，我们绘制了 SMM 结在固定平衡温度 $T=1$ K 和电压 $ V =1$ mV。清楚地表明，单个给定的 $\Delta B$ 对应于分子的两种可能的磁化强度。如果我们使用 $I_{\sigma }^{+-}$ 来表示 $\Delta B$ 从 $+5$ meV 扫描到 $ -5$ meV 和 $I_{\sigma }^{-+}$ 表示在相反方向扫描磁场时的电流（$\Delta B$ 从 -5 meV 变为 +5 meV)，那么 SMM 在 $+S$ 或 $-S$ 的两个自旋方向都可以在低-$\Delta B$ 区域（例如在点图 2c、d) 中的 C 和 D。在图 2c 中，小磁场区隧道电流的自旋极化系数 $\eta$ $\Delta B_{\Lambda _{-}}<\Delta B<\Delta B_{\ Lambda _{+}}$ 可以总结为

<图片>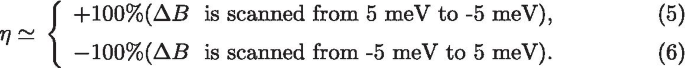

更重要的是，如图 2d 所示，我们注意到 $\Delta B=0$，即 C 点或 D 点处的隧道电流强度远大于大磁场区域下的隧道电流强度。 $V=1$ mV 的相同偏置电压。这意味着该器件在没有外部磁场的情况下更容易产生自旋极化的电子流，使其适合作为自旋滤波器或自旋存储器件。

为了讨论该分子结的自旋注入能力，我们将自旋-$\sigma$ 电流绘制为恒定栅极电压和较低温度下偏置电压的函数。图 3a、b 显示了 $I_{\uparrow (\downarrow )}$-V 在 $\Delta B=\pm 2$ meV 的大磁场值下的曲线（对应于图 2 中 A 和 B 点的磁场），而图 3c、d 显示了没有 \ (\Delta B\)（对应于图 2 中的 C 和 D 点）。无论选择哪种磁场方案，自旋过滤特征都是明显的。如图 3a（图 3b）所示，只有自旋向上（自旋向下）的电子可以流过结，而其他自旋方向的电子电流被 SMM 的自旋选择性完全抑制为零$+S$ ($-S$) 方向。当磁场 $\Delta B$ 从 $+S$ 和 $-S$ 方向减小为零时，在图 3c、d 中获得了类似的结果。在没有 $\Delta B$ 的情况下，SMM 必须被困在两个双稳态基态 $M=\pm S$ 之一。出于这个原因，SMM 的 $+S$ 和 $-S$ 自旋方向都可以在 $\Delta B=0$ 范围内得到很好的保留。例如，如果我们将 $\Delta B$ 从 $+5$ meV 扫描到零，则保存 $M=+S$，并获得完全极化的自旋电流（见图 3c））。此外，当偏置电压增加时，在没有外部磁场的情况下，电子电流比在大磁场的情况下更早地达到较高的电流平台。如图 3b、d 所示，尽管在 $\Delta B=0$ meV 和 $\Delta B=-\,2$ meV 状态中都没有自旋电流，$I_ {\downarrow }$ 图 3d 中的电流可以在 $V\approx 0.7$ mV 处达到 $0.5e \Gamma _{0}/\hbar$，同时在图 3c，需要更大的偏置电压至少 $V>1.5$ mV。

澄清图中的基础物理。 2 和 3，我们绘制分子状态概率 $P_{|0,\pm S\rangle }$, $P_{|0, S-1\rangle }$, $P_{|0, - S+1\rangle }$, $P_{|\uparrow , S+1/2\rangle }$, $P_{|\downarrow , -S-1/2\rangle }$, $ P_{|1, S-1/2\rangle }$ 和$P_{|1, -S+1/2\rangle }$ 作为$\Delta B$ 的函数，当扫描磁场时在 $T=0.5$ K 的固定平衡温度和 $V=1$ mV 的偏置电压下来回。在图 4a 中，$\Delta B$ 从 $-5$ meV 扫描到 $+5$ meV 的速度足够慢，以允许系统放松到稳态。结果表明，在大磁场范围 $\Delta B<-2$ meV 中，除了 $P_{|\downarrow , -S-1/2\rangle }=1 之外，所有状态的概率都为零$，这意味着 SMM 的自旋态固定在 $-S$ 方向，并且一个自旋向下的电子被外部磁场捕获在分子的 LUMO 能级中。对于相对较大的库仑排斥能值 ($U=25$ meV) 和被困在 LUMO 能级中的自旋向下电子，SMM 级不能存在自旋向上电子，并且电子电流被阻挡.当 $\Delta B$ 从 $-2$ meV 增加到 1 meV 时，出现非零分子态概率 $P_{|0,-S\rangle }$，并且电子电流由$\varepsilon _{|0,-S\rangle }\leftrightarrow \varepsilon _{|\downarrow , -S-1/2\rangle }$ 过渡。在这个 $\Delta B$ 窗口中，SMM 的自旋态仍然可以保存在 $-S$ 方向，但自旋向下的电子可以隧道穿过 SMM，从而产生纯自旋向下极化电子流.然而，当 $\Delta B$ 进一步增加到 $[1\,{\text {meV}}, 2\,{\text {meV}}]$ 的范围时，非弹性隧穿过程导致分子自旋发生磁转换。在这种情况下，SMM 的几乎所有自旋态都有机会被占据，两个特殊态 $P_{|0,-S\rangle }$ 和 $P_{|\uparrow ， +S+1/2\rangle }$，远大于其他任何状态。更有趣的是， $P_{|0,-S\rangle }=P_{|\uparrow , +S+1/2\rangle }$ 点恰好对应于点 $\Lambda _{+}\ ) 在图 2a 中，表明分子的磁化强度开始从 \(-S$ 反转到 $+S$。随着 $\Delta B$ 继续增加超过 2 meV，除了 $P_{|\uparrow , S+1/2\rangle }\rightarrow 1$ 之外，所有状态的概率都降低到零，这意味着 SMM 的自旋状态固定在 $+S$ 方向，并且隧道电流将被一个自旋电子阻挡分子的 LUMO 能级而“关闭”。另一方面，如果磁场从 $+5$ meV 扫描到 $-5$ meV（见图 4c），类似的过程将再次发生，反转点 $\Lambda _ {-}$ 对应于 $P_{|0,+S\rangle }=P_{|\downarrow , -S-1/2\rangle }$ 的点。在图 4b 中，我们展示了这些自旋状态的塞曼图。由于 SMM 的大磁各向异性，基态双峰具有量子数 $M =\pm S$ ($S=10$ for $\hbox {Mn}_{{12}}\ )-Ac) 通过 \(DS^{2}_{z}\约 60$ K 的能垒与激发态很好地分离。此外，磁开关点 $\Lambda _{(+)- }$ 在图 4 中大约等于 1.3 meV，它接近单个磁性原子中的反转点 $2S|{\mathcal {D}}|$。在图 4d 中，我们将分子状态概率绘制为固定温度 $T=0.5$ K 和磁场 $\Delta B=0$ 的偏置电压的函数。如果我们假设 SMM 被困在 $+S$ 自旋方向，那么图 4d 中的电子隧穿过程可以分为两部分：（i）在小偏置状态 $V<2.5\ ) mV，电子电流由 \(\varepsilon _{|0,+S\rangle }\leftrightarrow \varepsilon _{|\uparrow , S+1/2\rangle }$ 跃迁控制，并且只有自旋-向上的电子可以隧道通过结。 (ii) 当偏置电压增加到大偏置状态 $V>2.5$ mV 时，尽管偏置不足以克服自旋方向 $+S$ 和 $-S $，在$+S$ 方向具有更高能量的自旋态，例如$\varepsilon _{|0,+S-1\rangle }$ 和$\varepsilon _{|1,+S -1/2\rangle }$, 可以被占用，这将引入额外的额外通道用于自旋向下电子隧道穿过 SMM。结果，随着偏置电压的不断增加，隧穿电流将继续增加，但自旋极化系数$\eta$会降低。

最后，自旋向上电流 $I_{\uparrow }$ 和自旋向下电流 $I_{\downarrow }$ 的结果作为栅极电压（LUMO 能级的现场能量 $ \varepsilon _{0}$) 计算，有和没有外部磁场（见图 5）。在低温下，100$\%$ 自旋极化电子电流可以通过不同的栅极电压窗口“开/关”。当施加 $\Delta B=\pm 2$ meV 时，纯自旋$\sigma$ 电流出现在 $0.8\,{\text {meV}}<\varepsilon _ {0} <2.8\,{\text {meV}}$，而 $I_{\uparrow } =I_{\downarrow } =0$ 在这个范围之外。作为平衡温度T 增加，$I_{\sigma }$ 的峰值变低并变宽，但在低温下看到的高自旋极化电流仍然保持（见图 5a，b）。与大磁场区域不同，自旋$\sigma$ 电流在栅极电压窗口 $-0.8\,{\text {meV}}<\varepsilon _{0} <1.8\,{\text {meV}}$，并且自旋极化表现出两种不同的结果（见图 5c、d）。在栅极电压窗口$0.8\,{\text {meV}}<\varepsilon _{0} <1.8\,{\text {meV}}$, $\pm \,100\%$自旋极化电流可以在 V$=1$ mV 的小偏压下产生，对应于图 2c 中的 C 和 D 点。然而，在 $-0.8\,{\text {meV}}<\varepsilon _{0} <0.8\,{\text {meV}}$ 的栅极电压窗口中，状态之间的能隙 $ |0,\pm S \rangle$ 和 $|1,\pm S\mp 0.5 \rangle$ 变得非常小，$+S$（或 $- S$) 可以通过偏置电压达到自旋方向；因此，自旋向上和自旋向下的电子都可以穿过 SMM。因此，在该栅极电压范围内，电流的总自旋极化$\eta$降低。

结论

总之，我们提出了一种三态开关效应，具有用于自旋向上和自旋向下电流切换的两个“开启”状态以及电流“关闭”状态。这种自旋极化电流切换可以在 SMM（例如，$\hbox {Mn}_{{12}}$-Ac）隧道结中实现，并且由通过 LUMO 的自旋选择性单电子共振隧穿产生SMM。这种三态切换行为可以通过磁场和栅极电压来控制，无需自旋轨道相互作用或磁引线，是未来自旋电子电路中自旋滤波器或自旋存储器等自旋电子器件的良好候选者。

数据和材料的可用性

当前研究中使用的数据集可从本文的通讯作者处获得。

缩写

SMM：: 单分子磁铁
LUMO：: 最低未占分子轨道
Mn12-Ac：: [Mn12O12(CH3CO2)15(H2O)4]
TbPc2：: [(C32H16N8)2Tb^III ] 复杂

在 ZnO 纳米棒上掺杂 Mg 证明了通过分子对接分析改善了光催化降解和抗菌潜力用于水分解的增强型图案化助催化剂 TiO2/Fe2O3 光阳极

纳米材料