Dzyaloshinskii-Moriya 相互作用调制的磁化动力学在双界面自旋传递扭矩磁隧道结

介绍

磁性随机存取存储器 (MRAM) 具有低功耗、高密度、快速存取速度、几乎无限的耐用性以及与 CMOS 技术的良好兼容性，是下一代非易失性存储器最有希望的候选者之一 [1, 2]。 MRAM 的基本器件是磁隧道结 (MTJ)，它由夹在两个铁磁层（称为钉扎层和自由层）之间的隧道势垒组成。受益于垂直各向异性的进步，MTJ 的特征尺寸已缩小到 40 nm 甚至 1×nm 以下 [3,4,5]。然而，亚 40 nm MTJ 面临的挑战是保持足够的热稳定性屏障 E =μ 0M s H k V /2。 （与 μ 0 真空磁导率，M s 饱和磁化强度，H k 各向异性场，V 自由层的体积）。如该等式所示，E 随着 MTJ 的缩放而降低，从而导致数据保留时间的减少。为了克服这一挑战，提出了双界面 MTJ 以实现足够高的 E 在亚 40 nm 技术节点 [6,7,8,9,10]。通过使用两个耦合铁磁层作为复合自由层，等效体积 (V ) 在双界面 MTJ 中增加以增强热稳定性屏障。同时，减小阻尼常数以保持低开关电流。

在双界面 MTJ 中，铁磁/重金属 (FM/HM) 结构在优化性能方面起着重要作用。一方面，FM/HM 结构增加了自旋轨道耦合（SOC）以诱导垂直各向异性。另一方面，重金属作为复合自由层的两个铁磁层之间的间隔物，以提供 Ruderman-Kittel-Kasuya-Yosida (RKKY) 相互作用 [11]，其铁磁耦合两个铁磁层的磁化强度使它们表现得像一个相同的层。此外，最近的研究表明，重金属的强 SOC 与铁磁体的原子自旋结合可以形成一种称为 Dzyaloshinskii-Moriya 相互作用（DMI）的反对称交换耦合 [12, 13]。因此，在具有 FM/HM 结构的双界面 MTJ 中自然会产生 DMI。最近的研究证实，DMI 有利于手性磁性结构（例如，自旋螺旋、斯格明子和 Neel 型畴壁）并显着影响磁化动力学 [14,15,16,17,18,19,20,21 ,22,23,24,25]。值得一提的是，DMI 在双接口 MTJ 中的作用将变得更加复杂，因为需要同时考虑两个 FM/HM 接口以及额外的 RKKY 交互。因此，揭示DMI对双界面MTJ的影响具有重要意义。

在这封信中，我们首次研究了双接口MTJ在DMI和RKKY交互作用下的切换过程。双接口 MTJ 由自旋转移矩 (STT) 切换，这是 MRAM 数据写入的主流方法。最近有报道称 DMI 对 STT 切换有不利影响 [21, 22]。在这里，我们的结果表明，在双界面 MTJ 中，DMI 的不利影响可以通过 RKKY 交互来抑制，从而实现快速切换和更均匀的动态。我们的工作证明了双界面 STT-MTJ 对负面界面效应的鲁棒性。

方法

在这项工作中研究的器件如图 1a 所示，具有 FM/HM/FM 结构作为复合自由层。将 HM 层厚度调整为适当的值，以便感应的 RKKY 相互作用铁磁耦合两个 FM 层。 FM 层之一的磁性较软，表示为 FL1（自由层 1），而另一个磁性较硬，表示为 FL2（自由层 2）。为了切换复合自由层的磁化，向双界面 MTJ 施加电流并产生 STT。在这项工作中，我们只考虑从参考层传输到 FL1 的 STT，而忽略 FL1 和 FL2 之间的其他扭矩。这个简化的模型与之前报道的作品一致 [26,27,28]。 DMIs 在 FM/HM 和 HM/FM 界面都被诱导，并且由于不同的手性而具有相反的符号 [29]。

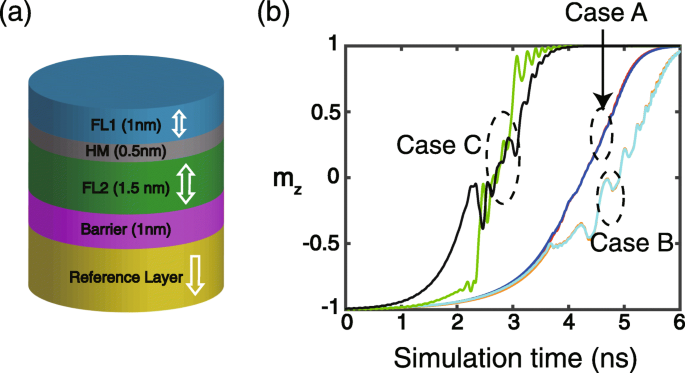
一 在这项工作中研究的设备的示意图结构。为清楚起见，未示出其他层。 b 时间相关 m 的典型结果 z （单位磁化的垂直分量）。情况A：σ =1 × 10 ⁻³ J/m ² , D 1 =D 2 =0（FL1 为红色，FL2 为蓝色）。情况B：σ =1 × 10 ⁻³ J/m ² , D 1 =1 mJ/m ² , D 2 =−1 mJ/m ² （FL1 为橙色，FL2 为青色）。情况C：σ =1 × 10 ⁻⁴ J/m ² , D 1 =D 2 =0（FL1绿色，FL2黑色）

通过微磁模拟研究了双界面 MTJ 中 FL1 和 FL2 的磁化动力学。单位磁化矢量的时间演变由以下 Landau-Lifshitz-Gilbert (LLG) 方程控制。我们选择开源微磁仿真工具 OOMMF 包 [30]，对器件结构进行建模并求解用于分析磁化动力学的 LLG 方程。

其中 γ 是旋磁比，m 是沿磁化强度的单位矢量，z 是沿厚度方向的单位向量，H eff 是有效场，包括单轴垂直各向异性、6-邻域交换能、DMI 场、RKKY 相互作用、退磁场、偶极相互作用和 STT。其他参数及其默认值列于表 1 中，除非另有说明。这些参数值符合最先进的技术。至于 DMI 量级，我们考虑双界面 MTJ 中的 CoFeB/W/CoFeB 复合自由层 [10, 31,32,33]。报告的 W/CoFeB 实验 DMI 结果从 0.12 mJ/m ² 到 0.73 mJ/m ² [34,35,36]。在我们的模拟中，我们将 DMI 幅度范围扩展到 ±2 mJ/m ² 一般研究。

一对磁矩之间的 RKKY 能量 m 我 和 m j 定义为 E ij =σ [1 − m 我 ∙ m j ]/Δ ij , 其中 m 我 和 m j 分别是 FL1 和 FL2 的磁矩。 σ 是两个表面之间的双线性表面交换系数。 Δ ij 是从像元 i 方向上的自由裁量像元大小 朝向单元格 j .在这项工作中，FL1 和 FL2 是铁磁耦合的，那么 σ> 0 这意味着 RKKY 相互作用趋于使 m 我 平行于 m j . DMI 作用于相邻的原子自旋 S 1 和 S 2 通过具有大 SOC 的第三个原子。对应的DMI哈密顿量表示为H DM =− D 12 ∙ (S 1 × S 2), 其中 D 12 是 DMI 向量 [37]。因此，DMI 降低了 S 之间的均匀性 1 和 S 2、与RKKY交互竞争。

结果与讨论

首先，时变m的典型仿真结果 z （单位磁化的垂直分量）如图 1b 所示。如果 RKKY 相互作用足够强（例如，σ =1 × 10 ⁻³ J/米 ² 在情况 A 和情况 B) 中，FL1 和 FL2 耦合在一起，因此无论是否考虑 DMI，它们的磁化动态几乎相同。还可以看出，DMI 的引入扭曲了磁化转换的过程（见案例 B），这与报道的结果 [21,22,23] 一致，并且可以归因于 DMI 的反对称交换。一旦 RKKY 相互作用不够强，FL1 和 FL2 的磁化动力学就不能理想地耦合，从而观察到它们之间的显着差异（参见案例 C）。下面，除非另有说明，否则模拟结果是在足够强的 RKKY 相互作用下获得的。

之后，我们研究了各种 RKKY 交互下的切换速度。 m 的时间反映了切换速度 z 达到 0（定义为切换时间）。 D 1 和 D 2 分别设置为正值和负值 [29]。相应的结果如图 2 所示。在没有 DMI 的情况下，切换时间随着增强的 RKKY 相互作用而增加，与其他报告的结果一致 [26,27,28,38]。原因是更强的 RKKY 相互作用使 FL1 和 FL2 的磁化动力学更加相干，这等效地增加了复合自由层的各向异性。然而，在 DMI 的存在下，切换时间对 RKKY 强度的依赖性变得更加混乱。这种混乱主要归因于 FL1 和 FL2 之间的各向异性不一致。稍后将给出更多解释。这些结果证明了 DMI 对双接口 MTJ 开关行为的影响不可忽略。

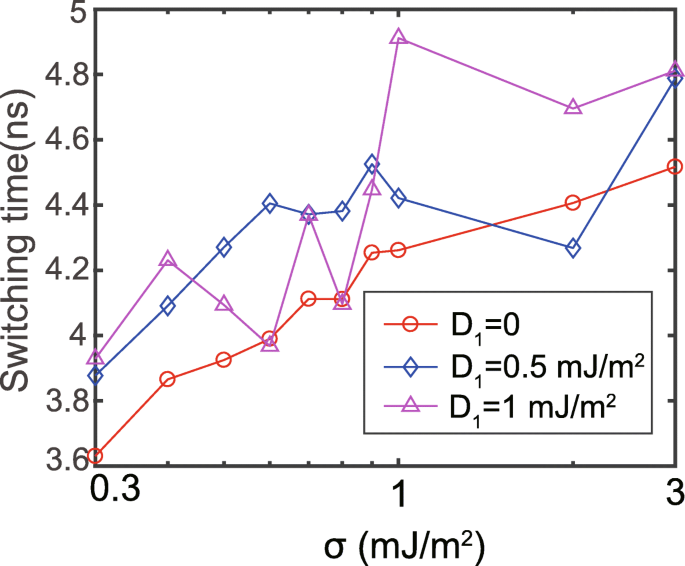
切换时间作为 RKKY 强度的函数，σ 以对数刻度表示。 D 1 和 D 2 设置为相同的值，但符号相反

接下来，我们更详细地研究 DMI 的影响。图 3 显示了作为 DMI 强度函数的切换时间。值得一提的是 D 1 和 D 2 在图 3a 中有意设置为相同的正值，尽管它们实际上具有相反的符号。换句话说，图 3a 对应于一个虚拟案例，我们研究它以验证模拟模型。从物理理论的角度来看，两个正 DMI 的不利影响是在铁磁耦合 RKKY 相互作用的作用下累积起来的。因此，预计切换时间会随着 D 的增加而增加 1 和 D 2，如之前的作品 [21, 22] 中所报道。该分析与图 3a 中显示的结果非常一致。从而验证了仿真模型的合理性。与图 3a 相比，如果 D 可以减轻 DMI 的不利影响 1 和 D 图 2 具有相反的符号，如图 3b 所示，其中开关时间的变化与图 3a 相比要小得多。请注意，在图 3b 中，曲线并不完全单调，稍后将解释局部波动。值得注意的是，可以通过适当调整 D 的大小来抵消两个界面上 DMI 的影响 1 和 D 2，如图3c所示。这些结果可以用手性理论解释如下。

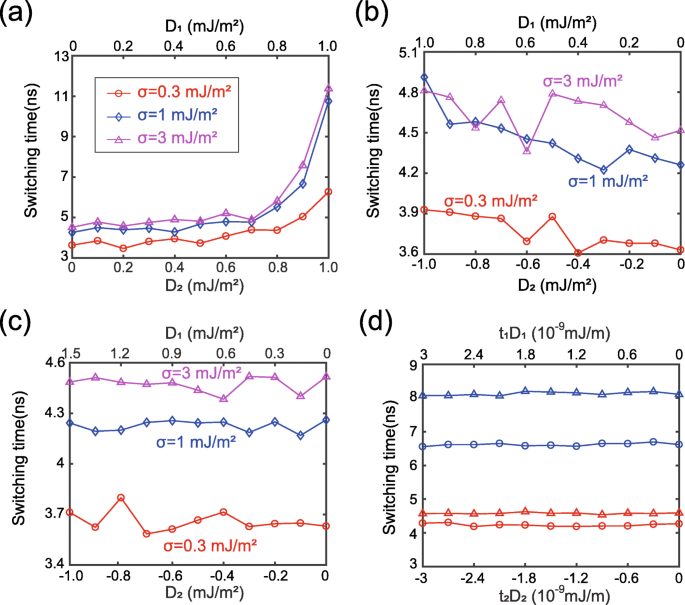
切换时间作为 DMI 强度的函数。 一 D 1 和 D 2 设置为相同的正值。 b D 1 和 D 2 设置为相同的值，但符号相反。 c D 1 和 D 2 配置为满足 t 1D 1 + t 2D 2 =0.d 改变厚度或各向异性常数时的附加结果，同时保持 t 1D 1 + t 2D 2 =0. 蓝线：t 1改为2 nm；红线：t 1 变为 1.5 nm。三角数据：σ =3 × 10 ⁻³ J/m ² .圆数据：σ =1 × 10 ⁻³ J/m ²

DMI 能量表示为 E DM =t ∬ D [米 x (∂m z /∂x ) − m z (∂m x /∂x ) + m 是 (∂m z /∂y ) − m z (∂m 是 /∂y )]d ² r =tDε DM [39]，其中 D 是连续 DMI 常数，t 是铁磁层的厚度。如上所述，在足够强的 RKKY 相互作用下，FL1 和 FL2 的磁化动力学几乎相同。在这种情况下，相同的 ε DM 在 FL1 和 FL2 中获得。那么FL1和FL2的总DMI能量可以通过E计算 全部 =(t 1D 1 + t 2D 2)ε DM .因此，通过设置 D 1/D 2 =− t 2/t 如图 1 所示，在 σ 足够大的情况下，FL1 和 FL2 的 DMI 效应可以完全抵消，与图 3c 一致。图 3d 中显示的附加结果进一步验证了这一结论，其中有意改变其他参数同时保持 D 1/D 2 =− t 2/t 1.

等效 DMI 幅度 (D 复合自由层的 eq) 可以表示为 D eq =(t 1D 1 + t 2D 2)/(t 1 + t 2)，可用于定量分析DMI对双界面MTJ的影响。为了验证该方程的有效性，我们在图 4a 中展示了两组模拟结果，其中在相同的 D 下获得了两条曲线 eq 但有两对不同的 {D 1, D 2} 值，分别。尽管两条曲线之间存在少许差异，但它们的总体趋势是相似的，并且验证了 DMI 对 STT 切换的不利影响。这里，两条曲线之间的差异可以解释如下。 FL1和FL2具有不同的各向异性常数，导致磁化动力学的局部不确定振荡，如图4c所示。在图 2 和图 3b 中也观察到了相同的现象。相反，理想情况如图 4b、d 所示，其中 FL1 和 FL2 的各向异性常数设置为相同的值。显然，可以看出两条曲线之间有很好的重合，表明 D 的上述表达式 eq 可以很好地描述双接口 MTJ 的等效 DMI 效果。

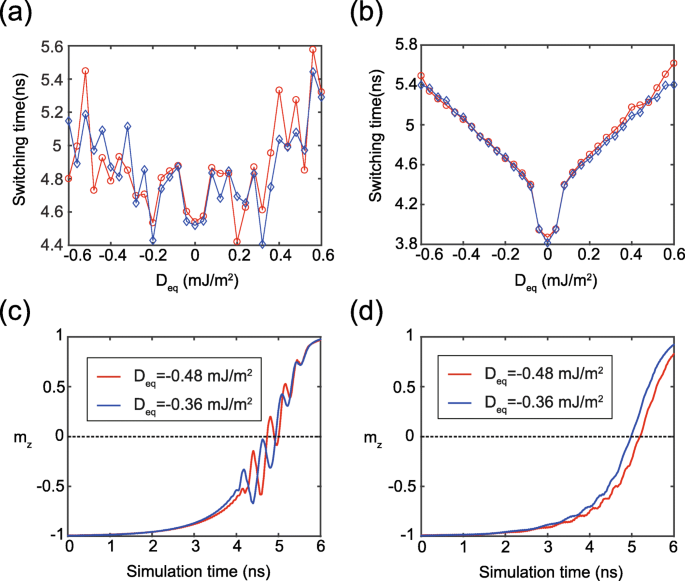
一 , b 切换时间作为 D 的函数 等式每个 D eq 是用两对不同的 {D 1, D 2} 根据 D 的值 eq =(t 1D 1 + t 2D 2)/(t 1 + t 2）。红色曲线：D 1 同时变化 D 2 固定为 1 mJ/m ² .蓝色曲线：D 1 和 D 2 始终设置为相同的值。这里σ =1 × 10 ⁻² J/m ² .在 a ，其他参数配置如表1。在b , K 你 1 =K 你 2 =0.7 mJ/m ³ 对于理想情况。 c , d 时间相关 m 的典型结果 z 对应于a 和 b , 分别

最后，我们更详细地分析了磁化动力学的时间演变。图 5 显示了磁化切换过程中与时间相关的能量。 FL1 和 FL2 的 DMI 能量被累积或抵消，取决于 D 的符号和大小 1 和 D 2. 这一趋势与上述理论模型非常吻合。此外，RKKY 能量保持在低值，这验证了 FL1 和 FL2 的磁矩是同步驱动的。 RKKY 和 DMI 场的分布如图 6 所示，其中 RKKY 场在各种情况下扮演不同的角色。首先，在非零 DMI 的情况下（参见案例 2 和案例 3），与零 DMI 的情况（参见案例 1）相比，RKKY 场强得多。可以理解，RKKY 场必须克服在 DMI 存在下磁纹理的额外不均匀性。二、如果D 1 和 D 2 是相反的符号，RKKY 场抵抗 FL1 和 FL2 中的 DMI 场（见案例 2）。因此，DMI 减弱，磁化动力学变得更加均匀。相反，一旦 D 1 和 D 2 具有相同的符号，RKKY 场在一个铁磁层中抵抗 DMI 场，但在另一个铁磁层中协助它（见情况 3）。因此整体DMI场对磁化动力学仍然有一定的影响，这验证了如果D，DMI不能被抵消 1 和 D 2个同号。

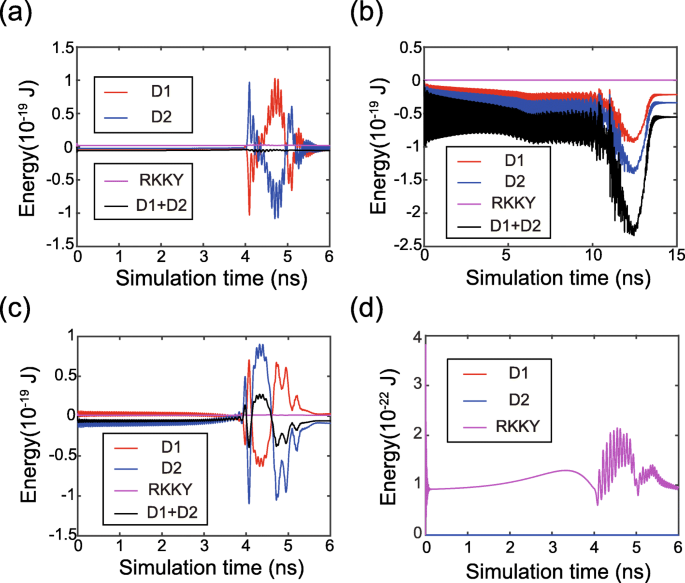
DMI 和 RKKY 能量的时间演化。 一 D 1 =1.5 mJ/m ² , D 2 =− 1 mJ/m ² ，即 DMI 效应被抵消。 b D 1 =D 2 =1 mJ/m ² ，即累积 DMI 效应。 c D 1 =1 mJ/m ² , D 2 =− 1 mJ/m ² ，即 DMI 效应被减轻但没有被抵消。 d D 1 =D 2 =0

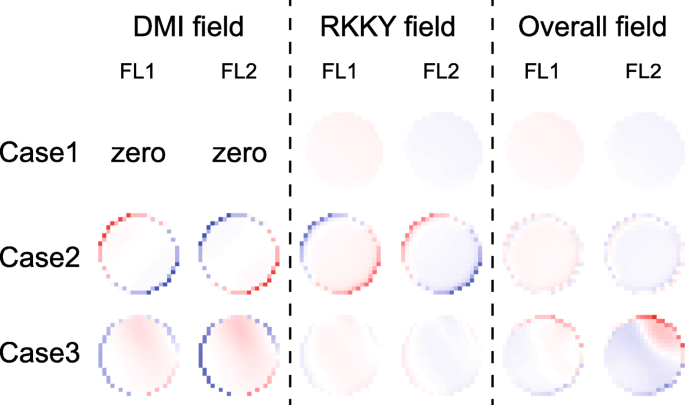
DMI 和 RKKY 字段的空间分布。这里显示了每种情况下某一时刻的典型结果。结论在其他时间点保持不变。案例 1：D 1 =D 2 =0. 情况 2：D 1 =1.5 mJ/m ² , D 2 =− 1 mJ/m ² ，即 DMI 效应被抵消。案例 3：D 1 =D 2 =1 mJ/m ² ，即累积DMI效应

图 7 显示了磁化切换期间 FL1 和 FL2 的微磁配置。尽管在所有情况下都会出现畴壁，但在某些时刻可以观察到不同的特征。众所周知，DMI 有利于非均匀磁性结构。尽管如此，在图 7 中，即使存在 DMI（见 m z =− 0.5 在情况 2) 中，只要 DMI 效应被抵消。该结果再次验证了上述理论模型。此外，还可以看出，如果 D 1 和 D 2 符号相同（见情况 3 总是出现畴壁），与上述分析一致。我们还展示了一些使用较小 MTJ 模拟的结果（见图 7 中的最后两行）。情况2（取消DMI）与情况3（未取消DMI）的微磁构型差异更为显着。

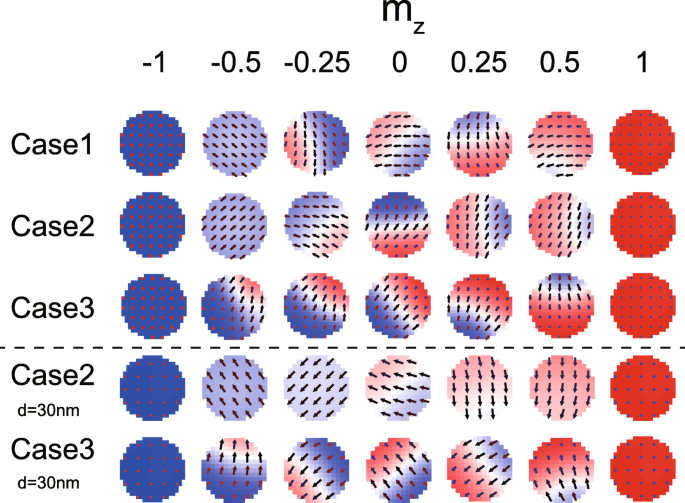
磁化切换期间的微磁配置。这里，案例1~3配置了与图6相同的参数

结论

我们全面研究了DMI对双接口STT-MTJ的影响。众所周知，双界面 MTJ 是为了增强热稳定性屏障而开发的。在这项工作中，我们的结果证明了双接口 MTJ 的另一个优势，即抑制 DMI 的不利影响。如果将两个铁磁层中的 DMI 配置为适当的值和相反的符号，它们可以被抑制甚至抵消，这自然由双界面 STT-MTJ 结构满足。提出了理论模型来解释该结论。讨论了微磁模拟结果，以揭示 DMI 在磁化动力学中的作用。我们的工作为最小化双接口STT-MTJ中的DMI提供了一种可行的方法。

数据和材料的可用性

所有数据完全可用，不受限制。

缩写

DMI：

Dzyaloshinskii-Moriya 互动

FL：

自由层

FM/HM：

铁磁/重金属

MRAM：

磁性随机存取存储器

MTJ：

磁性隧道结

RKKY：

鲁德曼-基特尔-Kasuya-Yosida

SOC：

自旋轨道耦合

STT：

自旋转移扭矩