维恩图和集
数学家使用维恩图 显示集合的逻辑关系 (对象的集合)彼此。也许您已经在代数或其他数学研究中看到过维恩图。如果你有,你可能还记得重叠的圆圈和联合 和交叉口 套。
我们将回顾维恩图的重叠圆圈。我们将采用术语 OR 和 AND 而不是并集和交集,因为这是数字电子产品中使用的术语。
维恩图将前一章的布尔代数与卡诺图联系起来。我们将把你已经知道的布尔代数与维恩图联系起来,然后过渡到卡诺图。
一套 是宇宙中对象的集合,如下所示。 成员 集合中包含的对象。集合的成员通常有一些共同点;不过,这不是必需的。
例如,在实数的宇宙中,所有正整数 {1,2,3…} 的集合是一个集合。集合 {3,4,5} 是较小集合或子集的一个例子 所有正整数的集合。另一个例子是大学生宇宙中所有男性的集合。你能想出更多集合的例子吗?
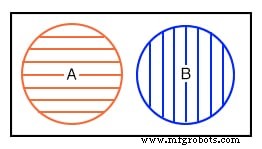
在左上方,我们有一个维恩图,显示了宇宙 U 内圆圈中的集合 A,即矩形区域。如果圆内的所有东西都是 A,那么圆外的任何东西都不是 A。因此,在中心上方,我们将圆 A 外的矩形区域标记为 A-not 而不是 U。我们在 a 中显示 B 和 B-not类似的方式。
如果 A 和 B 都包含在同一个宇宙中会发生什么?我们展示了四种可能性。

让我们仔细看看上面显示的四种可能性中的每一种。

第一个例子表明,根据维恩图,集合 A 和集合 B 没有任何共同点。 A 和 B 圆形阴影区域之间没有重叠。例如,假设集合 A 和 B 包含以下成员:
设置 A ={1,2,3,4} 集合 B ={5,6,7,8}
集合 A 的任何成员都不包含在集合 B 中,B 的任何成员也不包含在 A 中。因此,圆没有重叠。 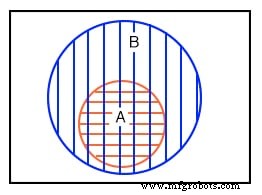
在上面维恩图中的第二个例子中,集合 A 完全包含在集合 B 中我们如何解释这种情况?假设集合 A 和 B 包含以下成员:
设置 A ={1,2} 集合 B ={1,2,3,4,5,6,7,8} 集合 A 的所有成员也是集合 B 的成员。因此,集合 A 是集合 B 的子集。由于集合 A 的所有成员都是集合 B 的成员,因此集合 A 完全绘制在集合 B 的边界内。
还有第五种情况,未显示,有四个例子。提示:它类似于最后一个(第四个)示例。为这第五种情况画一张维恩图。
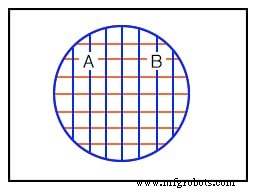
上面的第三个例子显示了集合 A 和集合 B 之间的完美重叠。看起来两个集合都包含相同的成员。假设集合 A 和 B 包含以下内容:
设置 A ={1,2,3,4} 集合 B ={1,2,3,4} 因此,
A组=B组
Sets And B 完全相同,因为它们都具有相同的成员。上面对应的维恩图中的 A 和 B 区域完全重叠。如果对上面的图案有任何疑问,请参考上图或下图,确定圆形区域重叠之前的样子。
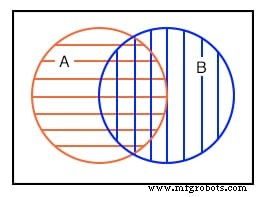
上面的第四个例子表明,重叠区域中的集合 A 和集合 B 之间存在一些共同点。例如,我们任意选择以下集合来说明我们的观点:
设置 A ={1,2,3,4} 集合 B ={3,4,5,6} 集合 A 和集合 B 都有共同的元素 3 和 4。这些元素是A和B共同的中心重叠的原因。我们需要仔细看看这种情况。
工业技术


