平行 R、L 和 C
我们可以从串联电路中取出相同的组件并将它们重新排列成并联配置,以获得简单的示例电路:
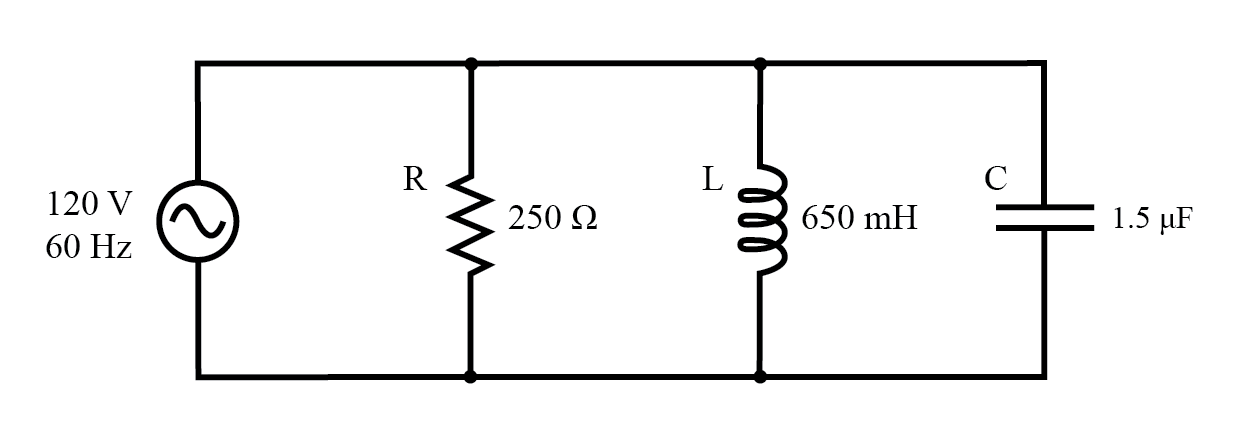
示例 R、L 和 C 并联电路。
并联组件中的阻抗
这些组件并联而不是串联的事实现在绝对不会影响它们各自的阻抗。只要电源的频率和以前一样,感抗和容抗根本不会改变。
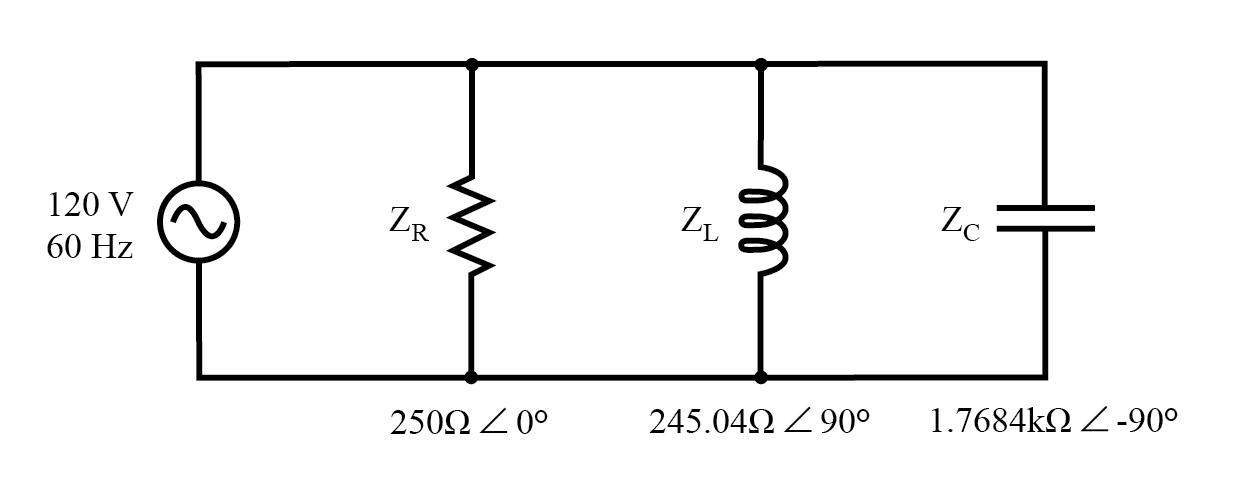
示例 R、L 和 C 并联电路,其中阻抗替换了元件值。
将所有元件值表示为阻抗 (Z),我们可以建立一个分析表并按照上一个示例问题进行处理,除了这次遵循并联电路而不是串联电路的规则:
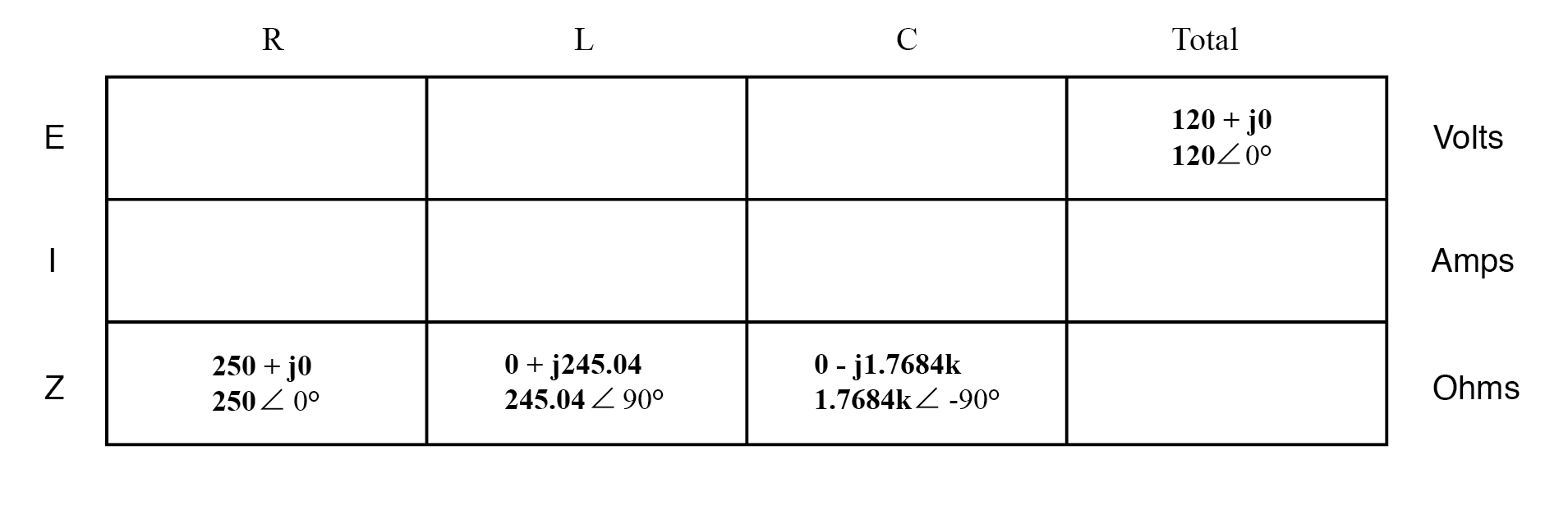
知道电压由并联电路中的所有组件平均分配,我们可以将总电压的数字转移到表中的所有组件列:
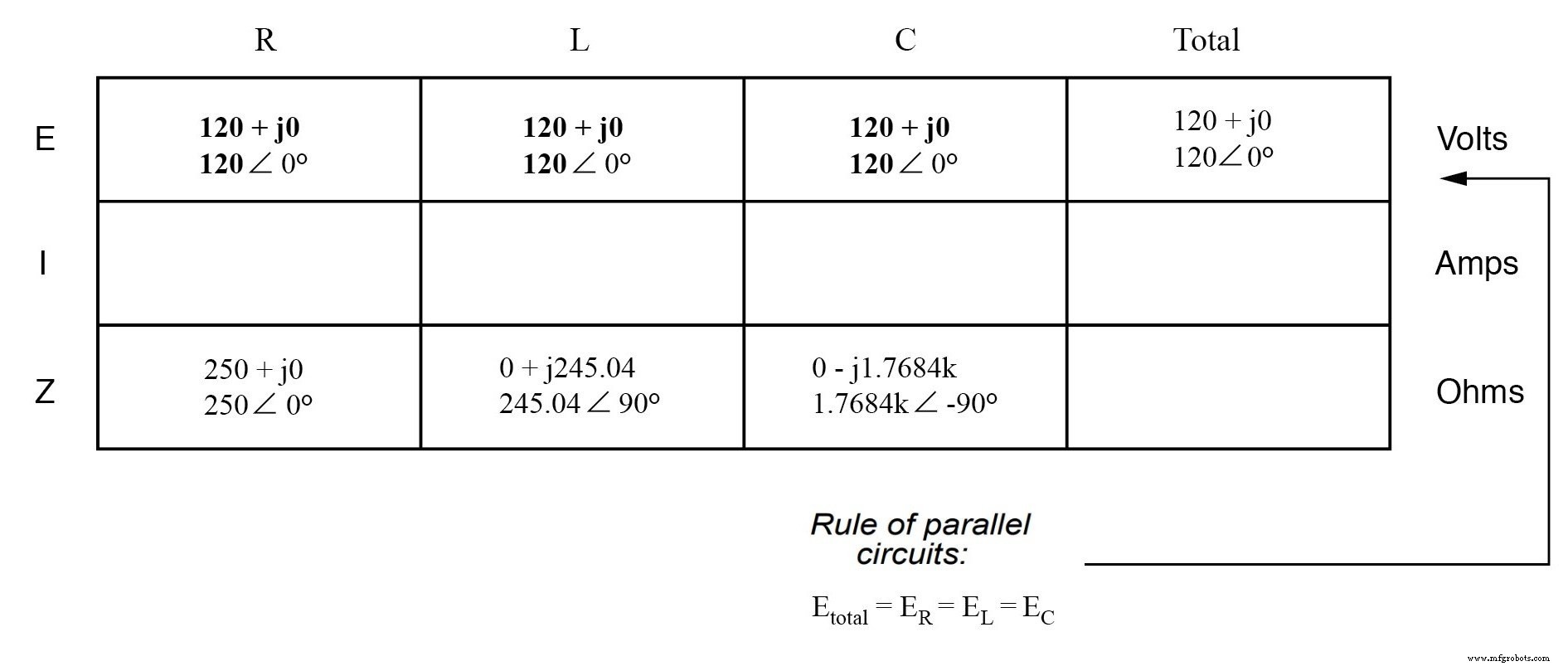
现在,我们可以在每一列中垂直应用欧姆定律 (I=E/Z) 来确定通过每个组件的电流:
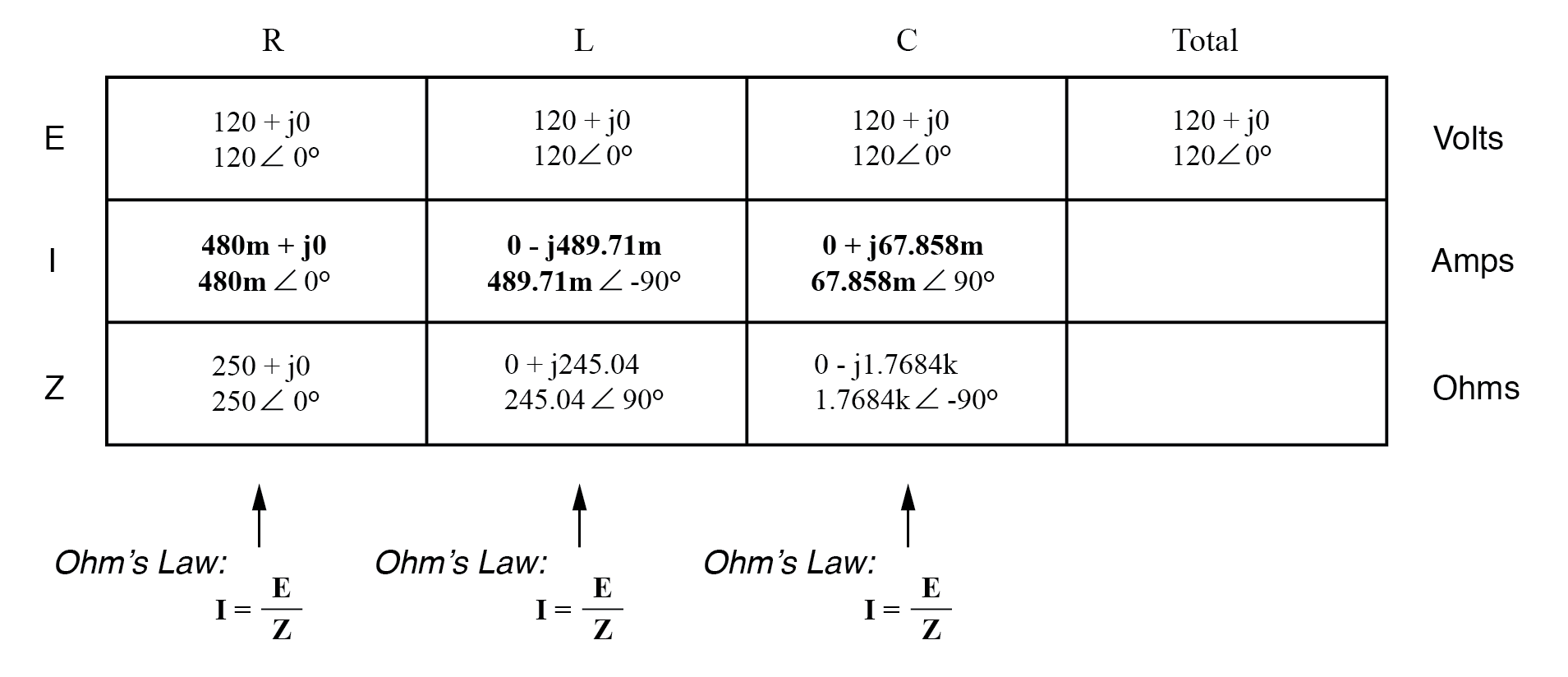
总电流和总阻抗的计算
有两种计算总电流和总阻抗的策略。首先,我们可以根据所有并联的单个阻抗计算总阻抗 (ZTotal =1/(1/ZR + 1/ZL + 1/ZC),然后通过将源电压除以总阻抗来计算总电流 (I=E/ Z).
然而,求解具有复数的并联阻抗方程并不是一件容易的事,所有的倒数(1/Z)。
如果您不幸没有处理复数的计算器并被迫手动完成所有操作(以极坐标形式交互各个阻抗,然后将它们全部转换为矩形形式以进行加法,然后转换回来),则尤其如此为最终反转的极坐标形式,然后反转)。
计算总电流和总阻抗的第二种方法是将所有支路电流相加得出总电流(并联电路中的总电流——交流或直流——等于支路电流的总和),然后使用欧姆定律从总电压和总电流确定总阻抗(Z=E/I)。
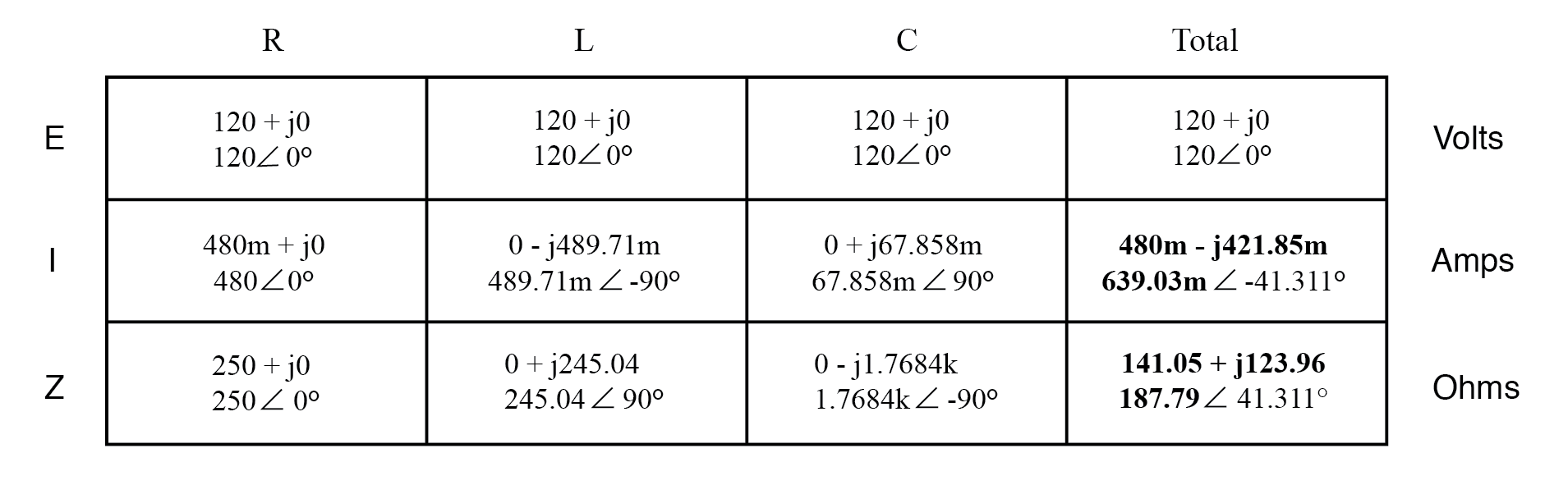
任何一种方法,如果执行得当,都会提供正确的答案。让我们试着用 SPICE 分析这个电路,看看会发生什么。
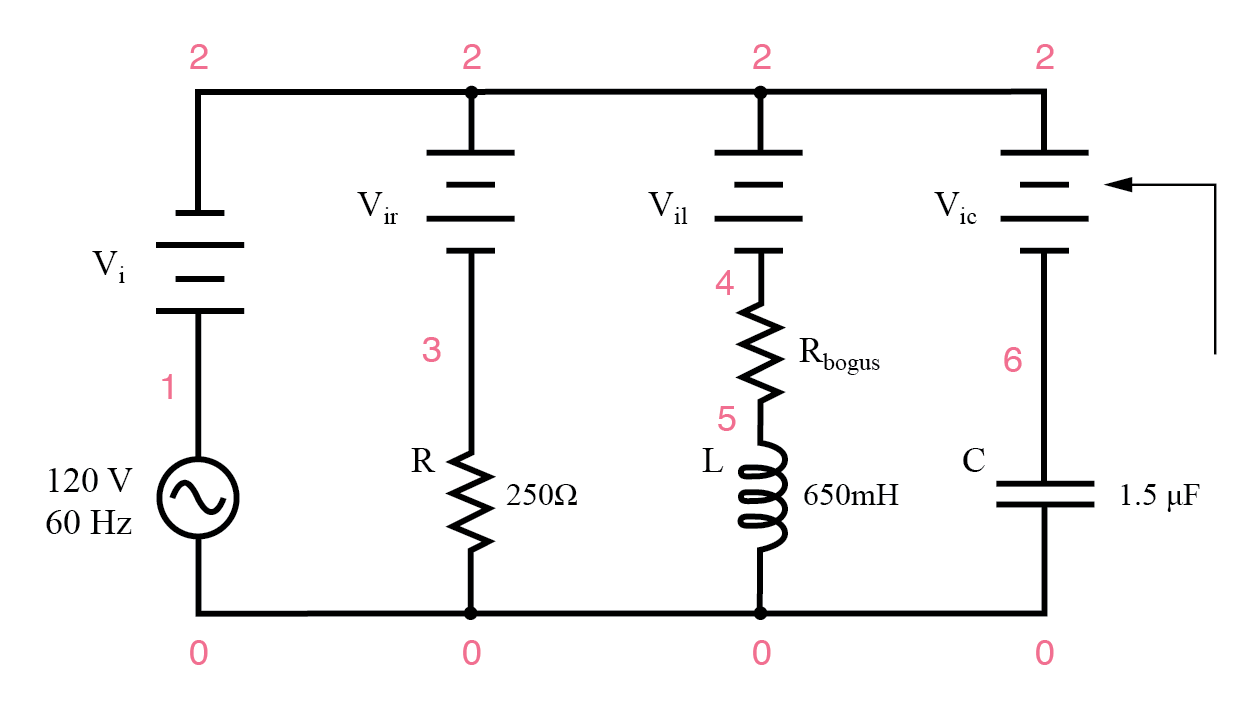
并联 R、L 和 C SPICE 电路示例。电池符号是 SPICE 用作电流测量点的“虚拟”电压源。全部设置为 0 伏。
ac r-l-c 电路 v1 1 0 交流 120 罪 六 1 2 交流 0 病毒 2 3 交流 0 vil 2 4 交流 0 rbogus 4 5 1e-12 维克 2 6 交流 0 r1 3 0 250 l1 5 0 650m c1 6 0 1.5u .ac 林 1 60 60 .print ac i(vi) i(vir) i(vil) i(vic) .print ac ip(vi) ip(vir) ip(vil) ip(vic) 。结尾
频率 i(vi) i(vir) i(vil) i(vic) 6.000E+01 6.390E-01 4.800E-01 4.897E-01 6.786E-02 频率 ip(vi) ip(vir) ip(vil) ip(vic) 6.000E+01 -4.131E+01 0.000E+00 -9.000E+01 9.000E+01

相关工作表:
- 串并联组合交流电路工作表
工业技术


