Δ-Y 和 Y-Δ 转换

在许多电路应用中，我们会遇到以两种方式之一连接在一起形成三端网络的组件：“Delta”或 Δ（也称为“Pi”或 π）配置和“Y”（也称为“T”）配置。

可以计算形成一种网络（Δ 或 Y）所需的电阻器的正确值，该网络的行为与另一种网络相同，仅从端子连接进行分析。也就是说，如果我们有两个独立的电阻网络，一个 Δ 和一个 Y，每个电阻网络都隐藏起来，只有三个端子（A、B 和 C）暴露用于测试，电阻的大小可以根据两个网络，因此无法从电气上确定一个网络与另一个网络的区别。换句话说，等效的 Δ 和 Y 网络表现相同。

Δ 和 Y 转换方程

有几个方程用于将一个网络转换为另一个网络：

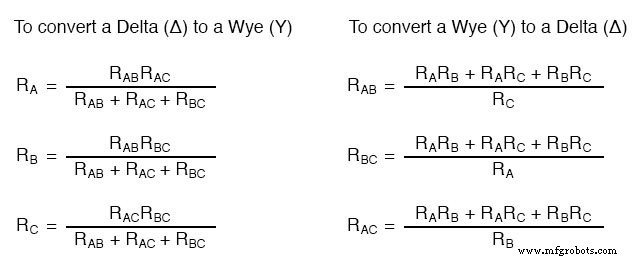
Δ 和 Y 网络在三相交流电源系统中经常出现（本系列丛书第二卷涵盖的主题），但即便如此，它们通常也是平衡网络（所有电阻值相等）和从一个到另一个的转换不需要涉及如此复杂的计算。一般技术人员什么时候需要使用这些方程？

Δ和Y转换的应用

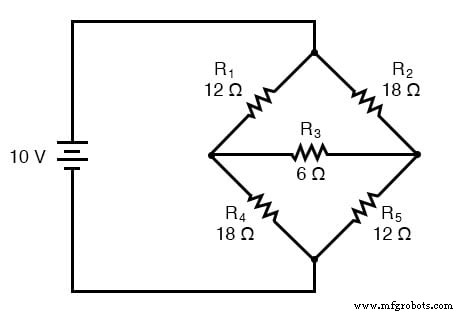
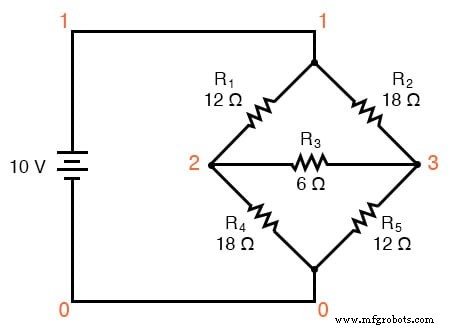
Δ-Y 转换的主要应用是在不平衡桥电路的解决方案中，如下所示：

该电路的分支电流或网状电流分析的解决方案相当复杂，米尔曼定理和叠加定理都没有任何帮助，因为只有一个电源。我们可以使用戴维宁定理或诺顿定理，将 R3 视为我们的负载，但这有什么乐趣？

如果我们将电阻器 R1、R2 和 R3 视为以 Δ 配置（分别为 Rab、Rac 和 Rbc）连接并生成等效的 Y 网络来替换它们，我们可以将这个桥接电路变成一个（更简单的）串/并联组合电路：

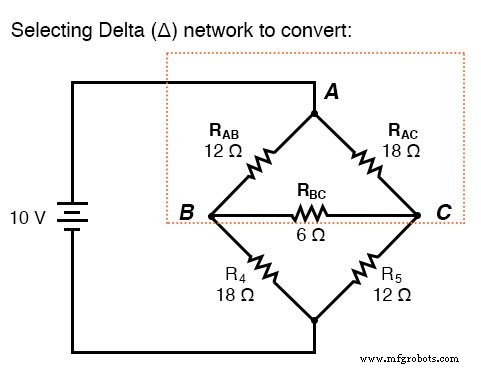
Δ-Y 转换后。 . .

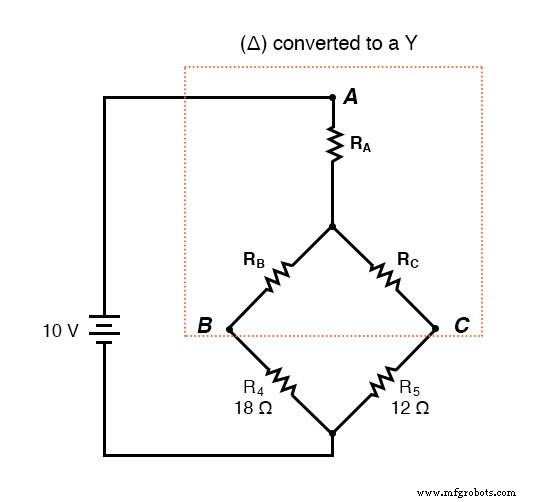
如果我们正确执行计算，转换后的电路中 A、B 和 C 点之间的电压将与原始电路中的相同，我们可以将这些值转换回原始桥配置。

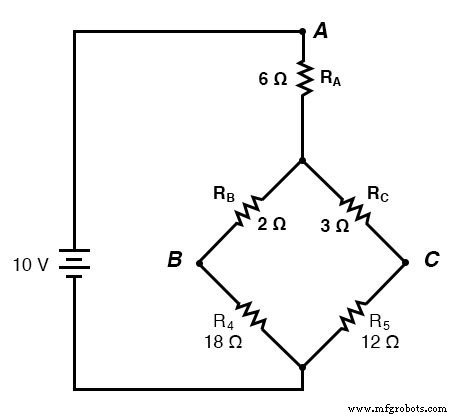
当然，电阻器 R4 和 R5 分别保持相同的 18 Ω 和 12 Ω。现在将电路分析为串联/并联组合，我们得出以下数字：

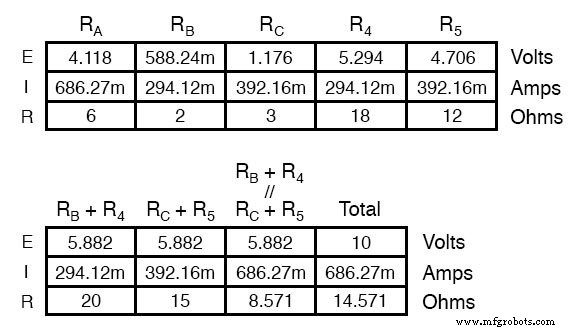
我们必须使用上表中的压降数字来确定 A、B 和 C 点之间的电压，看看它们如何相加（或相减，就像 B 和 C 点之间的电压一样）：

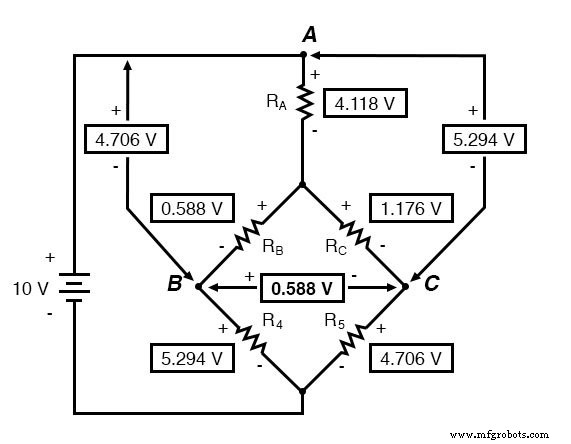
现在我们知道了这些电压，我们可以将它们转移到原来的桥式电路中相同的 A、B、C 点：

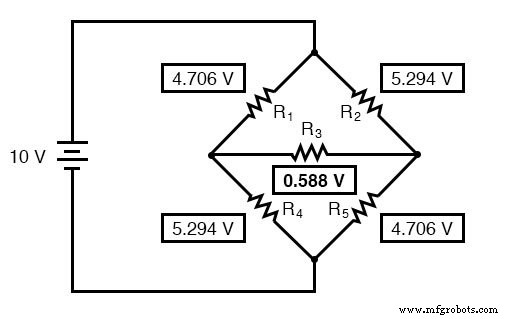
当然，R4 和 R5 上的压降与转换器电路中的压降完全相同。

此时，我们可以通过反复使用欧姆定律（I=E/R）来获取这些电压并确定电阻电流：

使用 SPICE 进行模拟

使用 SPICE 进行快速模拟将有助于验证我们的工作：

不平衡桥式电路 v1 1 0 r1 1 2 12 r2 1 3 18 r3 2 3 6 r4 2 0 18 r5 3 0 12 .dc v1 10 10 1 .print dc v(1,2) v(1,3) v(2,3) v(2,0) v(3,0) 。结尾 v1 v(1,2) v(1,3) v(2,3) v(2) v(3) 1.000E+01 4.706E+00 5.294E+00 5.882E-01 5.294E+00 4.706E+00 

从左到右读取的电压数字代表 R1 到 R5 五个相应电阻器上的电压降。我也可以显示电流，但由于这需要在 SPICE 网表中插入“虚拟”电压源，而且由于我们主要对验证 Δ-Y 转换方程而不是欧姆定律感兴趣，所以这就足够了。

评论：

• “Delta”(Δ) 网络也称为“Pi”(π) 网络。
• “Y”型网络也称为“T”型网络。
• Δ 和 Y 网络可以通过适当的电阻方程转换为它们的等效对应物。 “等效”是指从三个端子（A、B 和 C）测量的两个网络在电气上是相同的。
• 通过将桥接电路的一半从 Δ 转换为 Y 网络，可以将其简化为串联/并联电路。在解决了原始三个连接点（A、B 和 C）之间的电压降后，这些电压可以通过相同的等效点传输回原始桥接电路。

相关工作表：

• Delta 和 Wye 三相电路工作表