基于纳米环的等离子体透镜的偏振相关准远场超聚焦策略

背景

随着超分辨率成像[1]、粒子加速[2]、量子光学信息处理[3]和偏振相关光学数据存储[4]的发展，表面等离子体器件通过调制亚波长幅度的等离子体共振。等离子体透镜（PL）作为一种典型的器件，具有完美的成像能力，由 J. B. Pendry 在 2000 年首次提出 [5]，X. Zhang 等人通过实验证明了亚衍射极限光学成像。 5 年后[6]。然而，成像平面被限制在极近场，因为渐逝波呈指数下降，表明光场发散。这个限制使得它对于标准光学显微镜来说是不切实际的[7]。

近年来，已经研究了几种基于纳米结构的 PL [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]。这些 PL 不仅可以实现平面 [8] 或近场 [9] 的等离子体聚焦，而且还可以在远场 [10,11,12,13] 中具有聚焦能力，这通常由扫描光学成像显微镜 [14]。然而，这些 PLs 很难实现超出衍射极限的聚焦，直到金属-绝缘体-金属 (MIM) 波导的色散关系被用于基于纳米狭缝的 PLs 在亚波长尺度上调制相位 [11 , 15, 16, 17]。精确的相位调制有助于亚衍射极限焦线，并且线偏振光通常用作这些透镜的入射光。但是，通过简单地将类似的一维纳米狭缝透镜设计方法扩展到二维，当旋转对称的 PL 被线偏振光照射时无法实现圆形焦点 [18, 19]，表明强烈的偏振依赖性对焦性能。此外，焦距严重偏离了根据波前重建理论的数值计算，特别是对于基于纳米环的PLs[18]。

具有旋转对称性的基于纳米环的 PL，在以下讨论中为简单起见，被称为基于纳米环的等离子体透镜 (NRPL)，被认为是亚波长聚焦系统中转换折射透镜的替代品。但从表面等离子体激元 (SPP) 激发的角度来看，线偏振光不适用于 NRPL，因为激发效率与入射光的径向电场分量成正比。相比之下，具有圆柱对称偏振的径向偏振光适应NRPL的结构特性[25]。此外，利用环形孔径光阑 [26, 27] 或菲涅耳波带片 [28]，这种偏振光已被应用于实现亚波长圆形焦点。因此，径向偏振光通常用作 NRPL 的入射光 [20,21,22,23]。与使用空间滤波器的亚波长聚焦相比，这些 PL 具有调制亚波长波导中入射光相位的能力。表面等离子体 (SP) 波的激发可以增强电磁波的传输。然而，等离子体透镜在远场的超聚焦能力尚未得到证实。此外，虽然已经提出复合NRPL来调制焦距[24]，但未能有效控制焦距，电场能量仍然集中在透镜端面的中心。

在本文中，我们介绍了 NRPL 的理论设计和数值研究，重点是利用入射光的偏振特性实现超聚焦。我们在我们的研究中描述了 NRPL 的理论设计，并基于有限差分时域 (FDTD) 数值模拟提供了输出区域的聚焦性能。为了研究聚焦性能的偏振依赖性，线性、圆、方位角和径向偏振光都被考虑用于照明。我们讨论了输出区域的电场分布特征，包括亚衍射极限聚焦、焦点形状和焦距调制，并指出同轴条件对超聚焦性能的重要性。

方法

在这项工作中研究的 NRPL 是通过使用波前重建理论设计的，该理论广泛应用于基于纳米狭缝的 PL [11, 15]。为了在所需位置实现聚焦，光线通过i时引起的相对相位延迟 -基于几何光学，第一个纳米环需要满足以下条件：

其中 -Δϕ (r 我 ) 是内部中心的第一个纳米环与 i 之间的相对相位差 -th纳米环，r 是半径，λ 0 是入射光的自由空间波长，n 是一个任意整数，并且 f 0为设计焦距。

被调查的 NRPL 的基本组成元素是在金属膜中图案化的纳米环。根据参考文献。 [29]，当直径大于入射光的波长时，被金属壁包围的空气纳米环可以近似为 MIM 波导模型，如图 1 插图所示。相位延迟主要由实部定义传播常数β , 表示为 Re(β )•t , 其中 t 是纳米环的厚度。基于色散关系，复传播常数β 可以计算为：

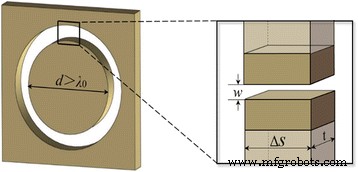
嵌入金膜中的单个纳米环的 MIM 波导模型。 插图 给出纳米环任意小部分的放大图

其中 k 0 代表真空中的波矢，ε d 和 ε 米 分别是电介质和金属的介电常数。基于方程。 (2) 可知，传播常数β 取决于纳米环的宽度。因此，对于具有给定厚度 t 的平面透镜 , 引起的相位延迟简单地由宽度 w 决定 当光穿过单个纳米环时。在我们的研究中，电介质设置为具有介电常数 ε 的空气 d =1，厚度为t的金膜 采用 400 nm，其在 650 nm 入射波长处的介电常数为 ε 米 =−12.8915 + 1.2044i [15]。此外，正如我们之前报道的 [16]，两个相邻 MIM 波导中传播光的耦合效应也对相位延迟起着重要作用，尤其是当间距金属壁小于趋肤深度的两倍时δ 米 ，可以通过[30]估计：

因此，计算出的趋肤深度δ 米 约为 28 nm。考虑耦合效应，超聚焦能力为0.38 λ的纳米狭缝PL 我们之前的研究报告了分辨率为 0 [16]。在这里，为了突出分析偏振态（SOP）对聚焦性能的影响，两个相邻纳米环之间的间隔壁被设计为 100 nm，远大于 2δ 米 消除耦合效应。

设计的 NRPL 的示意图如图 2 所示，总共包括 32 个同心纳米环来重建波前。所需相位调制的纳米环宽度范围为 10 到 100 nm。目标焦距f 0 是 1300 nm (2 λ 0）。为了有效地利用 MIM 波导模型，最内层纳米环的最小直径设置为 800 nm。此外，为了避免我们之前的工作 [15] 中讨论的焦点偏移，总相位差高达 10π，预测数值孔径 (NA) 为 0.96。因此，理论瑞利衍射极限，计算公式为 0.61 λ 0/NA [31]，是 413 nm (~0.64 λ 0).

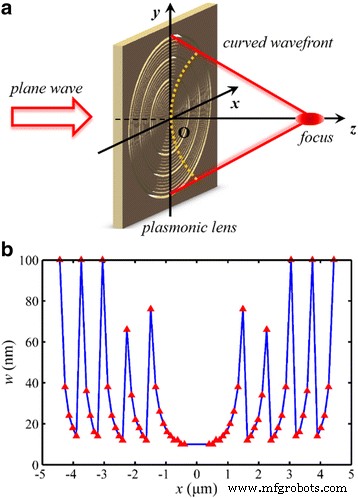
NRPL 的示意图。 一 入射光通常照亮镜头。 b 镜头的结构参数。 红色三角形的坐标值 表示半径 r 和宽度 w 相应的纳米环

为了研究入射光对空间强度分布的 SOP 影响，特别是聚焦性能，设计的 NRPL 分别被线性、圆形、方位角和径向偏振光照射。所有情况均通过FDTD数值模拟计算。根据矩阵光学，不同的偏振光可以用琼斯矩阵形式来描述，并应用相应的矩阵表达式来定义入射光。模型的边界是层数为 12 的完美匹配层 (PML)。为了平衡模拟中的计算精度和内存消耗，输出区域的网格大小设置为 10 nm，输出区域的网格大小设置为 5 nm。焦点区域。

结果

I 线偏振

对于线偏振光，SOP在空间上是均匀的，在这种情况下，电矢量的方向平行于x 轴。当光照射NRPL时，在总电场中存在两个相距400nm的焦点|E | ² 如图 3 所示。虽然两者的半高宽 (FWHM) 均为 210 nm (~0.32 λ 0) 在焦平面上，仿真结果表明强度分布明显不同于基于波前重建理论的设计，即在z上应该有一个圆形焦点 轴（也称光轴）。

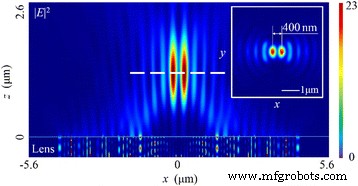
总电场强度分布图|E | ² 在线性偏振入射光的情况下。 插图 显示焦平面中的强度模式。焦距为 1215 nm（偏差为 6.54%）。两个焦点的 FWHM 为 ~0.32 λ 0，彼此相距 400 nm，焦深 (DOF) 为 ~1.68 λ 0

为了分析模拟和理论设计之间的差异，研究了电场分量的强度分布。如图 4 所示，在 x- 中出现椭圆形焦点和 FWHM 和 y- 方向为 220 nm (~0.34 λ 0) 和 457 nm (~0.70 λ 0)，分别。这种模式与参考文献的实验结果非常吻合。 [18] 应用相同的偏振光。然而，模拟表明 |E 的分布模式 | ² 类似于纵向分量的模式|E z | ² 占总电能的79.8%。因此，差异主要归因于|E的异常分布 z | ² .

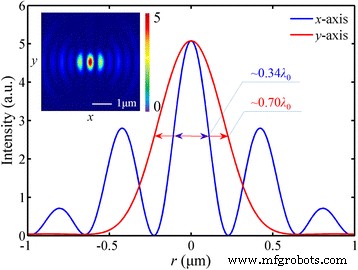
横向分量的强度分布|E r | ² 在焦平面。 插图 显示椭圆形焦点。焦距为 1425 nm（偏差为 9.62%）。 |E r | ² 占总电能的20.2%。自由度为 ~1.41 λ 0

这种现象最终可以用 NRPL 的传输特性来解释。一方面，金属和电介质界面处 SPP 的激发通常取决于入射光的局部偏振方向。横向电 (TE) 波不能对激发做出贡献。另一方面，由于 MIM 波导的亚波长结构，只有 SP 波可以通过该透镜传播 [32]。随着透镜的旋转对称，局部横向磁（TM）分量随方位角θ而变化 以余弦形式。因此，如图 5a 所示，|E 的强度分布 | ² ，刚好在透镜端面上方，集中在 y 附近 =0 区域 (−π/4 <θ <π/4)。相应地，坡印廷矢量在端面上沿径向传播，如图 5b 所示。因此，E 的矢量方向 基本平行于光轴，构成E的主要内容 z .由于对称相长干涉，焦平面上出现了两个焦点，而不是圆形焦点。

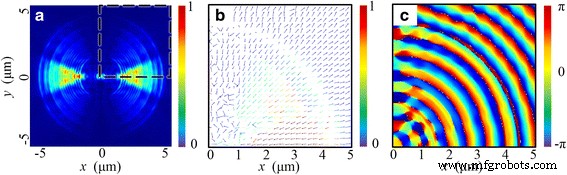
透镜端面上方 50 nm 处横截面的电场分布特性。 一 |E 的归一化强度分布 | ² . b 虚线内的坡印廷向量分布 a 中的区域。 E对应的相位分布 z

II 圆偏振

由于圆偏振光的状态随时间周期性变化，因此模拟结果为时均场分布。当透镜被这种偏振光照射时，在 |E 中形成一个甜甜圈状的焦点 z | ² .如图 6a 所示，该场中的焦距为 1185 nm，与设计值的偏差为 8.85%。甜甜圈的宽度为 210 nm (~0.32 λ 0)，半径为 400 nm。焦深 (DOF) 为 ~1.65 λ 0. |E的权重 z | ² 占总电能的80.6%。此外，在 |E r | ² ，空间域中的叠加生成具有 1405 nm 焦距的圆形焦点（偏差为 8.08%）。 FWHM 为 295 nm (~0.45 λ 0) 在这个领域，自由度是 ~1.68 λ 0. 此外，r-z 中的两种分布模式 平面类似于 x 中的那些 -z 在线性偏振入射光的情况下为平面。通过考虑径向电场分量，FWHM 可以减少到 222 nm (~0.34 λ 0).

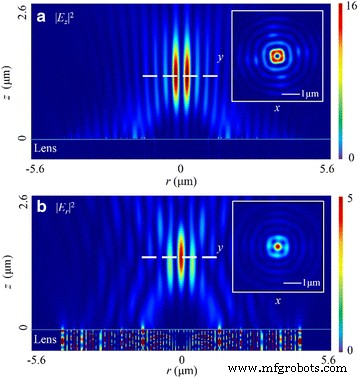
|E 的强度分布模式 z | ² 和 |E r | ² 在 r-z 在圆偏振光的情况下为平面。 一 在 |E z | ² , FWHM、DOF 和焦距为 ~0.32 λ 0, ~1.65 λ 分别为 0 和 1185 nm。 b 在 |E r | ² , FWHM、DOF 和焦距为 ~0.45 λ 0, ~1.68 λ 分别为 0 和 1405 nm

III 方位角偏振

对于方位角偏振的入射光，电矢量垂直于径向，平行于 NRPL 的金/真空界面。当方位偏振光照亮镜头时，局部 TE 波无法激发界面上的 SPP。因此，纳米环中的传输距离与其宽度成正比，如图 7 所示。由于结构和照明都是旋转对称的，因此仅显示了一半的强度分布模式和 NRPL 的结构。透射光可以忽略不计，输出区域没有明显的焦点。

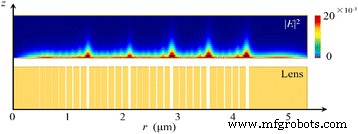
透镜区域的强度分布图及其横截面图。纳米环中非SP波的传输距离与狭缝宽度成正比

IV 径向极化

与方位偏振光相对应，径向偏振光可以被认为是局部TM波，这种偏振特性与SPPs的激发条件相匹配，这有助于在焦点处获得更高的最大强度。在总电场 E ，最大强度是线性偏振入射光的五倍。此外，还有一个圆形焦点，波长为 276 nm (~0.42 λ 0) |E 中的 FWHM | ² ，如图 8 所示。模拟的强度分布与高 NA 折射透镜的聚焦能力非常相似 [33]。此外，这种对焦性能仍然依赖于|E z | ² ，占总电能的82.0%。

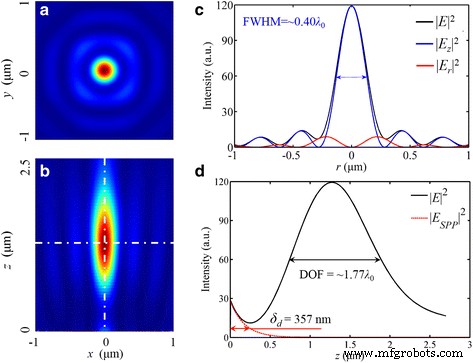
|E 的强度分布 | ² 在径向偏振入射光的情况下。 一 , b 焦平面和x中的分布 -z 横截面。 c 径向强度分布。 d 黑色实线沿光轴的强度分布 是模拟中的总电场强度分布和红色虚线 是 SPP 的计算曲线。焦距为 1275 nm（偏差为 1.92%）。 |E 的半高宽 | ² 和 |E z | ² 是 272 nm (~0.42 λ 0) 和 260 nm (~0.40 λ 0)，分别。自由度为 ~1.77 λ 0

与前一种情况不同的是，|E 中有一个圆形的焦点 z | ² .此外，该组件还决定了 |E 中的分布模式 | ² .如图 9a 所示，|E 中的 FWHM z | ² 是 260 nm (~0.40 λ 0) 在基于纳米狭缝的 PL [16] 的情况下，它接近焦线的焦线。特别地，焦距为1275nm。与设计值相比，相对误差降低到1.9%。然而，在|E中焦距为1455 nm（偏差为11.2%） r | ² .如图 9b 所示，有一个甜甜圈形状的焦点，宽度为 227 nm (~0.35 λ 0) 在这个领域。自由度为 ~1.60 λ 0.

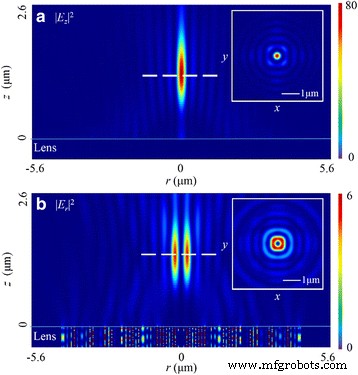
|E 的强度分布模式 z | ² 和 |E r | ² 在 r-z 在径向偏振光的情况下为平面。 一 |E z | ² r-z 中的模式 飞机。 插图 显示焦平面中的圆形焦点。 b 横向 |E r | ² r-z 中的模式 飞机。 插图 在焦平面上显示一个甜甜圈形状的焦点

研究了纳米环中 SP 波的相位延迟，如图 10 所示。模拟表明相位调制受 NRPL 结构参数的显着影响，入射面和输出面之间的模拟相位延迟为与基于方程的计算值基本相同。 (2).在透镜的端面上，SP波仍沿径向传播，表面中心有一个热点，其强度为聚焦强度的五分之一。 SP波的相长干涉，旋转对称分布，构造传播波，实现准远场圆形聚焦。

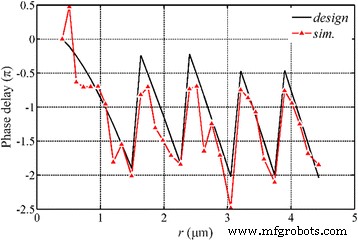
径向偏振入射光下NRPL的相位分析

讨论

NRPLs 的超聚焦能力

由于应用具有不同 SOP 的入射光，包括线性、圆形和径向偏振，可以实现亚衍射极限焦点。尽管焦点形状受 SOP 的影响，但这些焦点的特征尺寸都克服了瑞利衍射极限 (413 nm)。仿真结果成功证明了NRPL的超聚焦能力，焦平面内的强度分布与用于描述非衍射光束的贝塞尔函数相似。

对于径向偏振入射光的情况，如图11所示，|E中的强度分布 z | ² 与零阶贝塞尔函数 J 相同 0(K spp ⋅ n ⋅ r )，其中 n 和 r 分别是环境介质的折射率和到光轴的径向距离。焦点的 FWHM 略大于用 J 计算的主瓣尺寸 0. 特别是，模拟表明可以在准远场中实现非衍射光束。 SP波作为一种倏逝波，在远离出射面传播时呈指数下降，在真空中的传播距离可由[30]计算：

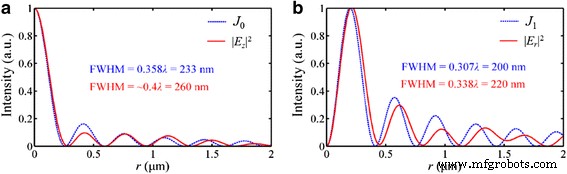
在径向偏振入射光下焦平面中 NRPL 的强度分布。 一 |E 的分布 z | ² 类似于零阶贝塞尔函数 J 0. b |E 的分布 r | ² 类似于一阶贝塞尔函数 J 1

其中 ε d 和 ε m 分别是电介质和金属的介电常数。因此，δ d 是 357 nm，这与图 8d 中所示的模拟一致。因此，在准远场区域可以忽略焦点处的SP波强度。

II 焦点形状

通过调制 SOP，可以在焦平面上实现椭圆形、圆形和环形焦点，如图 12 所示。该现象归因于亚波长焦距，我们无法实现圆形焦点同时聚焦电场和磁场。因此，在磁场（或​​电场）中实现了环形聚焦，而在相应的电场（或磁场）中实现了圆形聚焦。特别是由于没有纵向磁场，|H的强度分布 | ² 与|E的模式相同 r | ² .此外，|E z | ² 占总电能的80.0%左右，其规模不受入射光SOPs的影响。

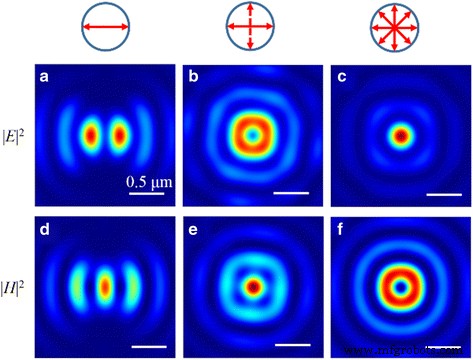
电场的归一化强度模式|E | ² 和磁场 |H | ² 当 NRPL 被偏振光照射时，在焦平面中。 一 |E | ² 和 d |H | ² 线偏振入射光的分布。 b |E | ² 和 e |H | ² 圆偏振入射光的分布。 c |E | ² 和 f |H | ² 径向偏振入射光分布

III 焦距调制

不同情况下的模拟焦距基本接近所需位置f 0 (1300 nm)，如表 1 所示。但是，我们意识到横向场中的焦距|E r | ² 比纵向场长约 200 nm |E z | ² ，无论入射光的SOP如何，偏差普遍存在。

理论上，波前重建理论适用于设计从近场到远场区域具有任意焦距的NRPL。然而，设计的等离子体透镜的实际焦距与设计的焦距是否吻合取决于透镜的总相位差。偏差可能归因于幅度型焦点和相位型焦点之间的区别[34]。由于 MIM 波导中的相位调制针对径向分量，因此 |E 中的焦距 r | ² 当满足至少 2π 的总相位差时，可以通过波前重建理论进行调制 [15]。对于纵向分量，较大的总相位差（>10π）有利于一致性。如图 13 所示，当相位差从 2π 增加到 16π 时，对应的 NA 为 0.75 到 0.96，|E 中的振幅型聚焦 z | ² 从镜头的输出表面移动到所需位置。作为|E的强度分布 | ² 由 |E 决定 z | ² ，NA 可以显着影响总电场中的焦距。但是，|E 中焦距的变化 z| ² 随总相位差的增大而逐渐减小。另一方面，|E 中相位型焦点的位置 r | ² 比较稳定。当应用具有高 NA 的 NRPL 时，基于 |E 的强度分布推导出的焦距仍然存在偏差 x | ² 和 |E z | ² ，并且偏差几乎保持不变。因此，NRPLs的焦距可以通过相位调制和结构优化来有效控制，尽管在横向和纵向分量场中不能达到相同的焦距。

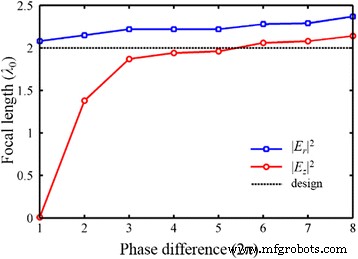
NRPL的焦距随总相位差从2π增加到16π

IV Focusing Performace in the Non-Coaxial Situation

The non-coaxial situation is a common problem in the experiment, and its effect on the focusing performance should be considered. As shown in Fig. 14, the center of the radially polarized light deviates 3 μm from the optical axis of the NRPL along the x axis. Compared with Figs. 8 and 9, the intensity distributions both in x-z cross section and in focal plane are apparently changed. In the longitudinal electric field, an elliptical focus is located at 1340 nm away from the exit surface of the lens. The FWHMs in x-z and y-z planes are 0.51 and 0.38 λ 0, respectively. On the other hand, the distribution in transverse field is also distorted, where the intensity of one side lobe is higher than the other one. Furthermore, compared with the coaxial condition, the decrease of the maximum intensity in the total electric field is more than 85%.

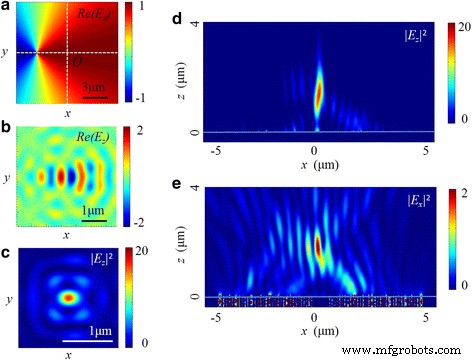
The intensity distribution of the NRPL in the non-coaxial situation. 一 The real part of E x of radially polarized incident light. b , c The distribution of Re(E z ) and |E z | ² in the focal plane. d , e The distribution of |E z | ² and |E x | ² in the x-z plane

The preliminary simulation indicates that the non-coaxial situation indeed influences the intensity distribution and the desired focusing performance of lens. Therefore, it is essential to guarantee the coaxiality between the incident light and the lens center during the experiment.

Conclusions

In summary, we build a NRPL with a high NA utilizing the wavefront reconstruction theory and the dispersion relation of the MIM waveguide. We also investigate the polarization-dependent focusing performance in the quasi-far field, including the focal length, FWHM, DOF, and the maximum intensity. The conventional polarized light, such as the linearly, circularly, radially, and azimuthally polarized light, are all considered. The simulations demonstrate the superfocusing capability of the designed NRPL. Utilizing the polarization-dependent property, the sub-diffraction-limit elliptical-, circular-, and donut-shape foci can be realized. However, one limitation of this work is that the proposed design strategy to realize the superfocusing performance of NRPLs is aimed for the quasi-far-field region, although to the best of our knowledge, the similar focusing capability in this region is rarely reported. In addition, we discover the underlying physical phenomenon on the focal shift and propose a more effective way to control the focusing position by employing both the transverse and longitudinal fields. There are considerable engineering applications for the nanoring-based superfocusing lenses, ranging from the super-resolution imaging, particle acceleration, quantum optical information processing to the optical data storage.

缩写

DOF:

Depth of focus

FDTD：

有限差分时域

FWHM：

Full-width at half maximum

MIM:

Metal-insulator-metal

NRPL:

Nanoring-based plasmonic lenses

PML:

Perfectly matched layer

SOP:

State of polarization

SPPs:

Surface plasmon polaritons

TE:

Transverse electric

TM:

Transverse magnetic