TiO2-水纳米流体在螺旋槽管中的流动和传热特性的实验研究

背景

纳米流体是一类具有优良传热性能的介质流体（例如ZnO-EG纳米流体[1]、Cu-CTAC/NaSal纳米流体[2]、MWCNTs-CTAC/NaSal纳米流体[3]），应用于各个领域如净水发电[4]、太阳能光热转换[5]、沸腾传热[6]。

纳米流体的对流传热是一种重要的传热过程，包括自然对流和强制对流传热。许多研究人员已经研究了纳米流体的自然对流热传递。李等人。 [7] 通过实验研究了填充有 ZnO-EG/DW 纳米流体的方形外壳的自然对流，得出的结论是高 EG 水溶液浓度不利于传热增强。胡等人。 [8] 通过实验和数值研究了方形外壳中 Al2O3-水纳米流体的自然对流，发现具有最高纳米颗粒分数的纳米流体会恶化传热。他等人。 [9]采用格子Boltzmann方法数值研究了方形外壳中Al2O3-水纳米流体的自然对流，结果表明传热性能随着纳米颗粒体积分数的增加而降低。齐等人。通过单相模型[10]和两相晶格玻尔兹曼模型[11]数值研究了不同长宽比外壳中Cu-镓纳米流体的自然对流；他们 [12] 还使用两相晶格 Boltzmann 模型研究了 Al2O3-水纳米流体的自然对流，结果表明，在较小纵横比外壳中的纳米流体具有更高的传热增强率。总之，观察到一些因素，例如高加热功率和纳米颗粒分数，有利于增强传热，而其他一些因素，例如外壳的大纵横比和低热导率的基液，可能导致以减少自然对流热传递。纳米流体的自然对流虽然在很多领域都有广泛的应用，但在高功率密度条件下无法满足高效散热。

与自然对流相比，强制对流换热具有更高的传热系数。研究人员采用了不同的实验方法来研究纳米流体的强制对流换热特性。孙等人。 [13, 14] 实验研究了Cu-水、Al-水、Al2O3-水、Fe2O3-水和Cu-水纳米流体在内置扭带外螺纹管中的流动和传热特性，发现Cu-水纳米流体表现出最佳的传热性能。杨等人。 [15]实验研究了Cu-水和Cu-粘弹性流体纳米流体在光滑管中的流动和传热特性，结果表明Cu-粘弹性流体纳米流体比粘弹性基础流体具有更高的传热性能但流动性较低电阻比铜水纳米流体。阿卜杜勒巴奇等人。 [16] 实验研究了 TiO2-BioGlycol/水纳米流体在扁平管中的传热增强，并建立了传热增强与摩擦系数之间的新关联，结果表明纳米流体的传热性能提高了约 28.2%比基础液。 Naphon[17]通过实验研究了TiO2-水纳米流体在水平螺旋盘管中的传热特性，发现纳米流体的传热性能随着曲率的减小和纳米颗粒分数的增加而增加。沙鲁尔等人。 [18] 以及 Kumar 和 Sonawane [19] 实验研究了三种纳米流体（Al2O3-水、SiO2-水和 ZnO-水）和两种纳米流体（Fe2O3-水和 Fe2O3-EG）在壳管式换热器，发现ZnO-水和Fe2O3-水纳米流体在各自的研究中表现出最好的传热性能。 El-Maghlany 等人。 [20]通过实验研究了Cu-水纳米流体在水平双管换热器中的传热特性和压降，结果表明纳米流体的传热增强随着纳米颗粒分数的增加而增加。桑达尔等人。 [21] 实验研究了 Fe3O4-水纳米流体在带有回弯管和线圈插入件的水平平管中的流动和传热特性，结果表明传热性能随着纳米粒子分数的增加和 p/d 比的降低而增加。线圈插入。以上研究主要集中在纳米流体在光滑管、扁平管、螺旋盘管或带线圈的管中的传热性能。

除上述实验研究外，还研究了纳米流体在螺旋波纹管中的强制对流换热特性。达齐等人。 [22, 23] 实验和数值研究了Al2O3-水纳米流体在螺旋波纹管中的湍流传热，结果表明，获得了比普通管更好的传热性能。达齐等人。 [24] 实验研究了 SiO2-水纳米流体在螺旋波纹管中的湍流传热特性，讨论了 5 个波纹节距对波纹管传热的影响，结果表明，小节距的波纹可以增加热量传输性能显着。帕克等人。 [25] 研究了热致变色液晶在螺旋槽管中的传热，结果表明，低雷诺数（30,000）下螺旋槽管与光滑管之间的传热增强比高于高雷诺数时的传热增强率。雷诺数（50,000 和 70,000）。以上研究主要研究了纳米流体在螺旋波纹管中的传热和流动特性。然而，对纳米流体在光滑管和螺旋槽管中的热工水力性能的综合分析有待进一步探讨。

上述研究对光滑管、带盘管的光滑管、换热器、螺旋波纹管等的流动和传热特性做出了很大贡献。该手稿的主要新颖之处主要包括以下几点：（1）利用紫外分光光度计建立了一种测试纳米流体稳定性的新方法（透射法），不同于已发表的参考文献广泛采用的沉淀法。透过率法的结果是可量化的，而沉淀法的结果是不可量化的； (2) 讨论了 TiO2-水纳米流体在光滑管和螺旋槽管中的热工水力性能综合评价，这方面的研究较少。有趣的是，发现最高雷诺数的纳米流体在螺旋槽管中可能没有最佳的热工水力性能，并且存在最佳热工水力性能的临界雷诺数。

方法

纳米流体制备和稳定性研究

选择二氧化钛作为纳米颗粒，选择水作为基液。图 1 显示了 TiO2 纳米颗粒。实验中TiO2-水纳米流体采用两步法制备，制备过程细节见图2。对于每个子步骤，机械搅拌时间为半小时，超声处理时间为 40 分钟。分散剂在水中的质量分数为6wt%，纳米流体的pH值为8。表1给出了纳米流体制备过程中部分材料的信息。从图 1 可以看出，纳米颗粒很容易聚集在一起。因此，使用已发表的参考文献广泛采用的沉淀法来研究纳米流体的稳定性。不同质量分数（0.1、0.3和0.5wt%）的TiO2-水纳米流体在不同静止时间的稳定性如图3所示，表明72h后纳米流体的稳定性仍然良好。

TiO2 纳米颗粒的形貌。 TiO2 纳米粒子的 TEM 图像：a 20 纳米，b 50 nm 和 c 100 纳米

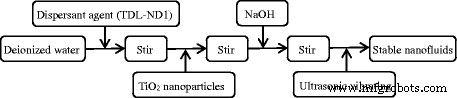
纳米流体的制备。 TiO2-水纳米流体的两步法制备工艺

纳米流体的稳定性观察。不同静止时间的TiO2-水纳米流体：a t =0 h，b t =48 h 和 c t =72 h

为了进一步检验纳米流体的稳定性，本文建立了一种利用紫外分光光度计测试纳米流体稳定性的新方法（透射法）。图 4 显示了透射率 (τ ) TiO2-水纳米流体的变化 (ω =0.3%) 与静止时间。不同剂量（M )的分散剂和不同pH值对纳米流体稳定性的影响。众所周知，如果纳米粒子在水中均匀分布，纳米流体会反射最多的光，从而导致纳米流体具有高反射率和低透射率。从图 4 可以看出，纳米流体 (ω =0.3%) 与 M =6 wt% 和 pH =8 的透光率最低。具有其他质量分数的纳米流体 (ω =0.1% 和 ω =0.5%) 均在 M 制备 =6 wt%，pH =8，纳米流体的透射率随ω变化趋势 =0.1% 和 ω =0.5% 与具有 ω 的纳米流体相同 =0.3%。因此，可以保证本文制备的纳米流体具有良好的稳定性。此外，通过研究分散剂和pH值对水的导热系数和粘度的影响，发现由于分散剂和NaOH较少，对它们的影响很小。

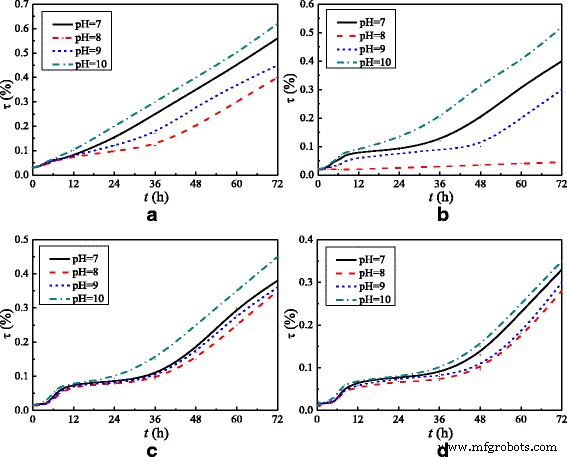
透射率 (τ ) 的纳米流体 (ω =0.3%）。 TiO2-水纳米流体的透光率随静止时间的变化(ω =0.3%) 不同剂量 (M ) 分散剂：a M =5 wt%，b M =6 wt%，c M =7 wt% 和 d M =8 wt%

图 5 显示了 TiO2-水纳米流体在不同温度和剪切速率下的热导率和动态粘度。发现本文中水的导热系数与Maxwell[26]有很好的一致性。可以发现，随着纳米粒子质量分数的增加，纳米流体的热导率增加，由于纳米粒子的高热导率，纳米流体的热导率比水增加了0.17-1.6%。此外，还发现热导率随温度升高而增加，因为高温增强了纳米粒子的布朗运动并提高了纳米流体的热导率。除了热导率的结论外，还可以发现，初始阶段的动态粘度随剪切速率的增加而增加，并随着剪切速率的增加而保持恒定，纳米流体的粘度与水相比增加了2.5-13.6%。这是因为在初始阶段添加到纳米流体中的小剪切力打破了流场的平衡并导致动态粘度增加（剪切增稠行为）。当流场再次达到稳态时，其动力粘度不变，与牛顿流体的特性具有很好的一致性。

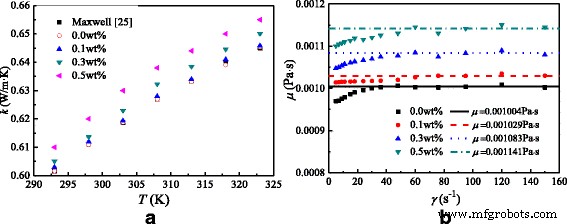
热导率和动态粘度。 TiO2-水纳米流体在不同温度和剪切速率下的热导率和动态粘度。 一 热导率b 动态粘度

实验系统

建立了螺旋槽管中TiO2-水纳米流体流动和传热特性的实验系统。图 6 表示实验系统的示意图。实验系统主要包括传热试验段、流阻试验段、温控水槽和泵。螺旋槽管由连接到直流电源的电阻丝加热。螺旋槽管的外壁温度由十个均匀分布在螺旋槽管表面的T型热电偶获得。螺旋槽管纳米流体的出口温度和入口温度由两个K型热电偶测量。所有热电偶都连接到数据采集仪器 (Agilent 34972A)。流阻采用压差仪测量。

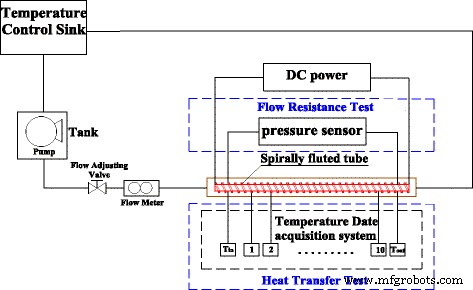
实验系统。实验系统示意图

螺旋槽管详图见图7。光管和螺旋槽管材料均为不锈钢，等效直径相同，长度均为1200mm，试验断面均为管中段1000mm，管两端各留100mm，避免入口效应。

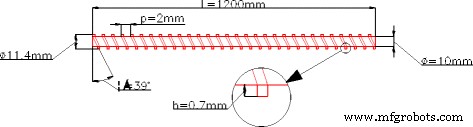
螺旋槽管。螺旋槽管详图

计算公式

加热电源由直流电源提供：

其中 \( {Q}_{\begin{array}{l}0\\ {}\end{array}} \) 是加热功率，U 是电压，I 是电流。

流体吸收的热量计算如下：

其中 Q f 是流体吸收的热量，c p 是流体的比热，q m 是质量流量，T 出和T in分别为流体出口温度和入口温度。

热容量如下：

其中 c p 是纳米流体的热容，φ 为纳米颗粒体积分数，下标“bf”代表基液，下标“p”代表纳米颗粒。

流体平均温度计算如下：

其中 T f为管内流体的平均温度。

管子外壁平均温度如下图所示：

其中 T ow 是管子的外壁平均温度，T w(i )为贴在管外壁的热电偶温度，有十个热电偶均匀贴在管外壁。

管子内壁平均温度可按下式计算：

其中 T iw 为管内壁平均温度，r o 和 ri 分别是管子的外半径和内半径，λ 是管的热导率，l 是管子的长度。

对流传热系数计算如下：

其中 h f 是对流传热系数，d e为管子当量直径。

努塞尔数计算如下：

其中 Nu 是努塞尔数和 λ f为热导率测量仪测得的管内流体的热导率。

雷诺数如下所示：

其中 Re 是雷诺数，ρ 是流体的密度，u 是流体的速度，μ f为超级旋转流变仪测得的流体动态粘度。

纳米流体的密度如下所示：

其中 ρ 是纳米流体的密度，φ 是纳米颗粒的体积分数，ρ bf 是水的密度，ρ p是纳米颗粒的密度。

流体的摩擦阻力系数表示为：

其中 f 是摩擦阻力系数，\( \frac{\varDelta p}{\varDelta l} \) 是单位长度的压降。

传热与流动阻力综合评价方程如下[27]：

其中 ς 为综合评价指标。

不确定性分析

实验误差是由实验系统中设备的精度引起的。对应的误差方程如下：

其中直流电源的精度为 ± 5.0%，热电偶的精度为 ± 0.1%，努塞尔数的误差可由式(13) 并且约为 ± 5.0%。压力传感器的精度为 ± 0.5%，长度的精度为 ± 0.1%，质量流量的精度为 ± 1.06%，摩擦阻力系数的误差由式(14) 并且约为 ± 1.29%。

结果和讨论

实验系统验证

在对纳米流体进行实验研究之前，需要进行实验系统验证。选择水作为传热介质。本文实验结果与已发表文献结果之间的努塞尔数和摩擦阻力系数见图 1。 8 和 9。它可以从图。由图 8 和图 9 可以看出，不同雷诺数下的努塞尔数和摩擦阻力系数分别与已发表文献 [28, 29] 和 [30, 31] 的结果吻合较好。 Nusselt数和摩擦阻力系数在层流和湍流下的最大误差分别约为3.5%、2.8%、2.1%和2.1%，验证了实验系统的准确性和可靠性。并且发现图8b中Dittus-Boelter的结果高于过渡流下的实际结果，因为经验公式仅适用于强湍流区，这与文献[28]的结果一致.进一步证明了本文结果的有效性。

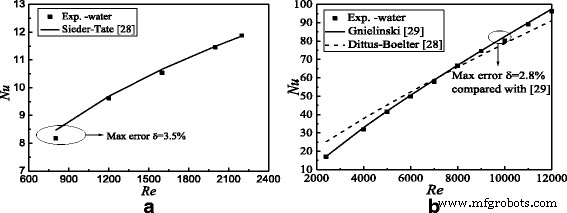
传热特性验证。实验结果与文献结果的努塞尔数比较。 一 层流b 湍流

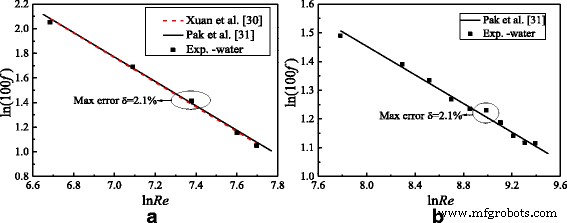
流量特性验证。实验结果与文献结果的摩擦阻力系数比较。 一 层流b 湍流

实验结果和讨论

研究了TiO2-水纳米流体在光滑管中的流动和传热特性。图 10 显示了填充有不同雷诺数的纳米流体的光滑管的努塞尔数。对于层流和湍流，努塞尔数随着雷诺数和纳米颗粒质量分数的增加而增加。流体的湍流度随着雷诺数的增加而增加，这减少了层流边界层并改善了传热。在基液中加入更多的纳米粒子会导致整体热导率的增加，这也改善了传热。此外，[32, 33] 其他因素包括纳米颗粒布朗运动的增加、接触角的减小、非均匀剪切速率、颗粒形状和聚集对传热增强也有很大影响。在之前发表的论文 [11] 中，讨论了布朗力和颗粒尺寸对传热增强的影响。发现布朗力是纳米粒子间相互作用力中最大的力，有利于强化传热，小粒径也有利于强化传热。从图 10a 可以看出，从水到 ω 的传热增强比 =0.1 wt% 纳米流体显示最大，但纳米流体的传热增强率来自ω =0.1 wt% 至 ω =0.3 wt%开始下降，纳米流体的传热增强率从ω开始 =0.3 wt% 至 ω =0.5 wt% 见证了最小的一个。如图 5 所示，与水相比，纳米流体的热导率和粘度分别增加了 0.17-1.6% 和 2.5-13.6%。对于层流，由于速度低且纳米颗粒很少，因此粘度对传热的影响很小，然后从水到ω的热导率起主要作用 =0.1 wt% 纳米流体。然而，随着纳米颗粒分数的增加，与热导率的增加相比，粘度的增加更为显着，这导致传热增强率降低。对于湍流，发现具有不同纳米粒子质量分数的纳米流体的传热增强是接近的。这是因为湍流在传热增强中起主要作用，纳米粒子质量分数的影响变小。此外，还可以发现，与湍流相比，纳米流体在层流中表现出更大的传热增强率。纳米粒子质量分数在层流中对传热增强起主要作用，并且随着纳米粒子质量分数的增加，它表现出较大的传热增强。然而，在湍流中纳米颗粒质量分数对传热增强的影响变小，湍流强度起主要作用；因此，与层流相比，随着纳米颗粒质量分数的增加，湍流中的传热增强率更小。

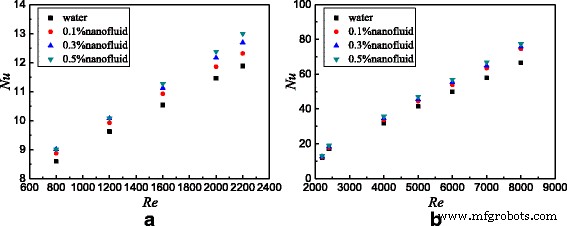
光滑管中的努塞尔数。填充有不同雷诺数的纳米流体的光滑管的努塞尔数。 一 层流b 湍流

基于图10的数据，图11显示了光滑管中纳米流体与水的努塞尔数比。可以发现具有ω的TiO2-水纳米流体 =0.5 wt%, ω =0.3 wt%，并且 ω =0.1 wt% 与光滑管中的水相比，层流的传热分别提高了 11.2、7.4 和 4.5%，湍流的传热最多分别提高了 16.1、13.9 和 11.9%。

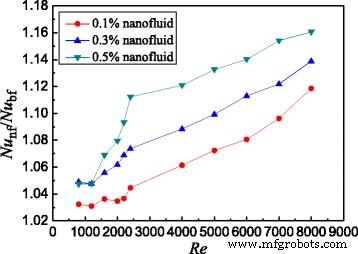
光滑管中的努塞尔数比。光滑管内纳米流体与基液的努塞尔数比

除了研究TiO2-水纳米流体在光滑管中的传热特性外，还研究了流动特性。图 12 显示了填充纳米流体的光滑管的摩擦阻力系数和压降。从图 12 中可以看出，摩擦阻力系数随着雷诺数的增加而减小，因为雷诺数的增加导致速度的增加，根据方程，速度与摩擦阻力系数成反比。 (9) 和 (11)。发现压降随着摩擦阻力系数的增加而减小，因为压降与雷诺数成正比，而摩擦阻力系数与雷诺数成反比。因此，压降与摩擦阻力系数成反比。此外，从图 12 中可以发现，摩擦阻力系数随着纳米颗粒质量分数的增加而增加，但在不同纳米颗粒质量分数之间增加很小。对于具有 ω 的 TiO2-水纳米流体 =0.5 wt%, ω =0.3 wt%，并且 ω =0.1 wt% 在光滑管中，与光滑管中的水相比，摩擦阻力系数分别在层流和湍流中分别增加了 7.9、5.2 和 3.0%，在湍流中增加了 2.5、1.5 和 0.6%。将纳米颗粒加入水中会导致粘度增加，这与摩擦阻力系数成正比。然而，摩擦阻力主要是由螺旋槽管的螺旋结构引起的，纳米颗粒对摩擦阻力的影响远小于螺旋结构，导致不同纳米颗粒质量分数的差异很小。 <图片>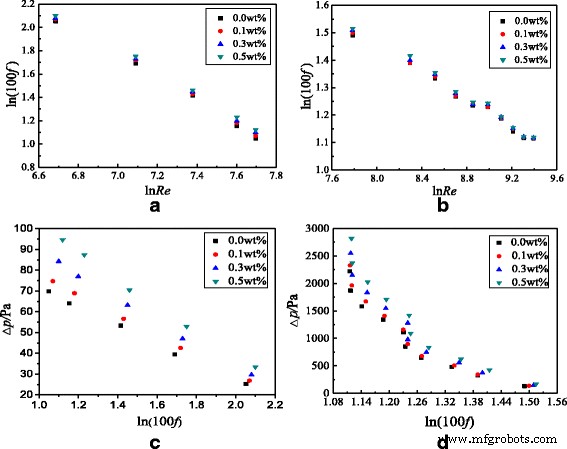

Frictional resistance coefficients and pressure drop in the smooth tube. Frictional resistance coefficients and pressure drop of the smooth tube filled with nanofluids. Frictional resistance coefficients:a laminar flow and b turbulent flow; pressure drop:c laminar flow and d turbulent flow

Above studies are on smooth tube, and the flow and heat transfer characteristics of water and TiO2-water nanofluids in the spirally fluted tube will be investigated in the following text. Figure 13 presents the Nusselt numbers of the spirally fluted tube filled with TiO2-water nanofluids at different Reynolds numbers. It obtains a similar conclusion in the spirally fluted tube (Fig. 13) similar to that in the smooth tube (Fig. 10). It is found that the Nusselt number increases with the Reynolds number and nanoparticle mass fraction. The differences between the spirally fluted tube and smooth tube are that there is a larger heat transfer enhancement in the spirally fluted tube than that in the smooth tube, which is due to the screw structure of the spirally fluted tube.

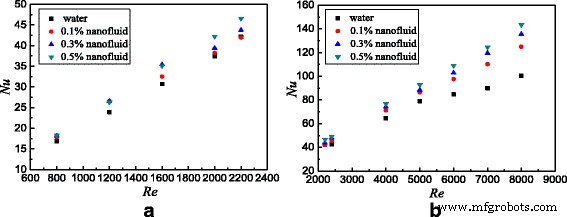
Nusselt numbers in the spirally fluted tube. Nusselt numbers of the spirally fluted tube filled with nanofluids at different Reynolds numbers. 一 Laminar flow b Turbulent flow

Based on the data of Fig. 13, Fig. 14 shows the Nusselt number ratios of nanofluids to the water in the spirally fluted tube. Figure 14 shows that TiO2-water nanofluids with ω  = 0.5 wt%, ω  = 0.3 wt%, and ω  = 0.1 wt% can enhance the heat transfer by 14.7, 12.6, and 11.3% for laminar flow and 42.8, 35.4, and 24.6% for turbulent flow at best compared with water in the spirally fluted tube, respectively. There is a larger increase in heat transfer for turbulent flow than that for laminar flow.

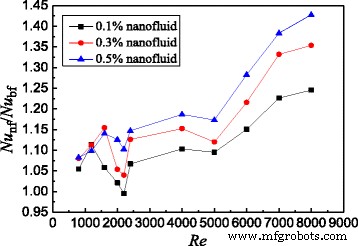
Nusselt number ratios in the spirally fluted tube. Nusselt number ratios between nanofluids and base fluid in the spirally fluted tube

The flow characteristics of TiO2-water nanofluids in the spirally fluted tube are also studied. Figure 15 presents the frictional resistance coefficients and pressure drop of the spirally fluted tube filled with nanofluids, which shows that the frictional resistance coefficient decreases with the Reynolds number and increases with the nanoparticle mass fraction, and the pressure drop decreases with the frictional resistance coefficient. The reasons are similar to that in the smooth tube (Fig. 12c, d). TiO2-water nanofluids with ω  = 0.5 wt%, ω  = 0.3 wt%, and ω  = 0.1 wt% can enhance the frictional resistance coefficients by 20.2, 16.5, and 12.5% for laminar flow and 10.5, 7.7, and 2.0% for turbulent flow at best compared with water in the spirally fluted tube, respectively. There is a smaller increase in frictional resistance coefficients for turbulent flow than that for laminar flow.

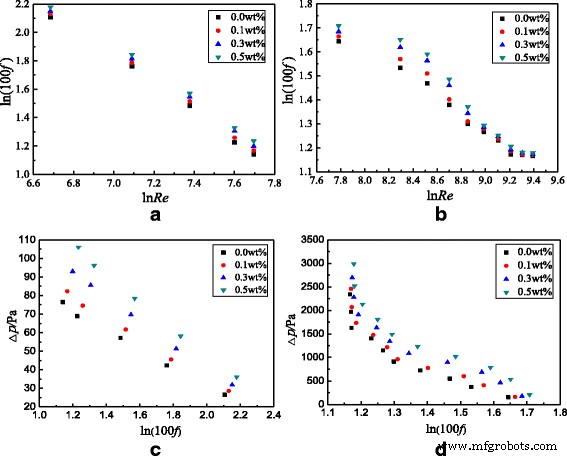
Frictional resistance coefficients and pressure drop in the spirally fluted tube. Frictional resistance coefficients of the spirally fluted tube filled with nanofluids. Frictional resistance coefficients:a laminar flow and b turbulent flow; pressure drop:c laminar flow and d turbulent flow

The heat transfer characteristics of TiO2-water nanofluids in the smooth tube and spirally fluted tube are investigated in this paper separately. Figure 16 shows the comparison of Nusselt numbers between the smooth tube and the spirally fluted tube filled with nanofluids at different Reynolds numbers. It can be found that TiO2-water nanofluids with ω  = 0.5 wt%, ω  = 0.3 wt%, and ω  = 0.1 wt% in the spirally fluted tube can enhance the heat transfer by 257.9, 245.1, and 240.7% at best compared with TiO2-water nanofluids in the smooth tube, respectively. Also, TiO2-water nanofluids with ω  = 0.5 wt%, ω  = 0.3 wt%, and ω  = 0.1 wt% in the spirally fluted tube can enhance the heat transfer by 291.3, 268.8, and 253.1% at best compared with water in the smooth tube, respectively. TiO2-water nanofluids in the spirally fluted tube have a larger enhancement than that in the smooth tube.

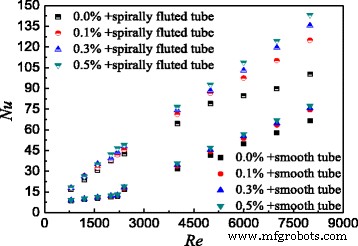
Comparison of Nusselt numbers in two tubes. Comparison of Nusselt numbers between the smooth tube and spirally fluted tube filled with nanofluids at different Reynolds numbers

In order to synthetically analyze the thermo-hydraulic performance of TiO2-water nanofluids in the smooth tube and spirally fluted tube, Fig. 17 presents the comprehensive analysis of nanofluids in the smooth tube and the spirally fluted tube based on the Eq. (12). It can be found that the highest comprehensive evaluation index ξ for spirally fluted tube is about at Re  = 2300 which is the critical Reynolds number between laminar flow and turbulent flow. The increases of the Nusselt number and frictional resistance coefficients are mainly due to the nanoparticles, the Reynolds number, and the screw structure of spirally fluted tube. For spirally fluted tube, due to the screw structure, the increase of the Nusselt number is larger than the increase of frictional resistance coefficients at small Reynolds number (Re  ≤ 2300); conversely, the increase of the Nusselt number is smaller than the increase of frictional resistance coefficients at big Reynolds number (Re  > 2300). Also, the comprehensive evaluation index ξ for the smooth tube increases with the Reynolds number. The increase of the Nusselt number is always larger than the increase of frictional resistance coefficients because the smooth tube has no screw structure. The conclusions of Fig. 17 are very important for the choices of tubes and Reynolds numbers in the heat-exchange equipment considering the comprehensive evaluation of the thermo-hydraulic performance. For the smooth tube, the higher Reynolds number can be chosen due to the factor that the thermo-hydraulic index always increases with the Reynolds number. While for the spirally fluted tube, the appropriate Reynolds number for the highest thermo-hydraulic index is about 2300.

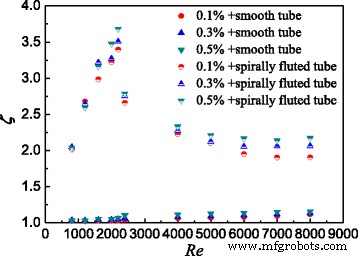
Comprehensive analysis of the two tubes. Comprehensive analysis of nanofluids in the smooth tube and the spirally fluted tube

结论

The flow and heat transfer characteristics of TiO2-water nanofluids in a spirally fluted tube are experimentally studied. Some conclusions are obtained as follows:

1. (1)

    TiO2-water nanofluids with different nanoparticle mass fractions are prepared, and TiO2-water nanofluids with M = 6 wt% and pH = 8 have the lowest transmittance and show the best stability.

2. (2)

    For TiO2-water nanofluids in the spirally fluted tube, there is a larger increase in heat transfer and a smaller increase in frictional resistance coefficients for turbulent flow than that for laminar flow.

3. (3)

    TiO2-water nanofluids in the spirally fluted tube have a larger enhancement than that in the smooth tube. TiO2-water nanofluids in the spirally fluted tube can enhance the heat transfer by 257.9% at best compared with that in the smooth tube.

4. (4)

    The highest comprehensive evaluation indexes of TiO2-water nanofluids in the spirally fluted tube and smooth tube are different. For the spirally fluted tube, the highest comprehensive evaluation index ξ is at Re  = 2300 which is the critical Reynolds number between the laminar flow and the turbulent flow. For the smooth tube, the comprehensive evaluation index ξ increases with the Reynolds number.