通过尺寸、修饰、缺陷和掺杂设计和调整石墨烯功函数：第一性原理理论研究

背景

作为一种具有多种优异性能的材料，石墨烯 [1,2,3] 已广泛应用于不同领域，如传感器、场效应晶体管 (FET)、光伏器件电极、肖特基二极管、真空管、和发光二极管的金属-半导体结，并已成为许多材料的替代品 [4,5,6,7]。石墨烯可以解决场效应管的小型化问题和光伏器件的成本，同时保持良好的稳定性和电性能。然而，石墨烯功函数 (WF) 对这些电子设备的性能具有至关重要的影响。因此，了解和控制石墨烯的 WF 对于基于石墨烯的电子设备具有重要意义。通常，FET 器件的性能可以由源/漏电极的 WF 决定 [8,9,10]。由于金属-半导体接触后材料的WF差异，界面中将存在电位差，这对肖特基或欧姆接触有直接影响[10]。鉴于两种不同材料的能带排列由其各自的WFs决定，控制石墨烯WF是减少接触势垒的关键[11]。

通过实验测得的石墨烯 WF 约为 4.2 到 4.8 eV [12, 13]。费米能级的变化会导致 WF 的变化。许多实验和理论分析表明，石墨烯的费米能级可以通过芳香族和气体分子的有意掺杂 [14, 15] 或紫外线照射 [16]、表面功能化 [17, 18]、缺陷 [19] 和静电来调节。门控 [20]。例如，袁等人。发现石墨烯的 WF 通过吸附 Na 和 Cl 发生显着变化 [21]。张等人。表明通过用碱金属阳离子覆盖石墨烯，WF 可以在 4.0-4.5 eV 的范围内微调 [22]。 Leenaerts 等人。了解了石墨烯的内在特性。结果表明，少层石墨烯的 WF 几乎与层数无关，但可以通过偶极层进行调制 [23]。沃洛丁等人。和彭等人。使用机械方法改变石墨烯WF [24]。他们都发现WF会随着应变而增加。余等人。使用电场效应来调整石墨烯的 WF，并证明在环境和干燥氮气条件下，WF 可以在 4.5-4.8 eV（单层石墨烯）和 4.65-4.75 eV（双层石墨烯）范围内调整 [25]。石等人。发现可以通过控制浸入时间来调节石墨烯薄膜的表面电位。对于小于 20 秒的掺杂时间，表面电位单调增加到约 0.5 V [13]。此外，发现辐照是控制掺杂浓度的有效方法。斯特拉基斯等人。通过调整激光曝光时间，控制掺杂和反应水平，将 GO-Cl 层的 WF 从 4.9 eV 调整到最大值 5.23 eV [26]。然而，康等人。通过直接表面功能化调节氧化石墨烯的WF[27]。

虽然之前的许多研究已经报道了控制石墨烯WF的方法，但研究结果还不够全面。例如，关于不同手性石墨烯对 WF 的尺寸效应的比较研究并没有提供足够的信息。此外，石墨烯的修饰和缺陷对 WF 的影响仍然不是很清楚。虽然研究了掺杂对石墨烯WF的影响，但没有提到相应的掺杂原子形成能。例如，在 Shi 的实验中，将石墨烯浸入 AuCl3 溶液中以调节 WF [13]；然而，WF 与掺杂浓度之间的关系仍不清楚。此外，必须指出的是，官能团的位置和缺陷对石墨烯 WF 的影响尚未见报道。鉴于 WF 的控制方法成本高昂，必须研究不同方法的内在特性。

在本文中，通过第一性原理理论对WF的控制方法进行了综合研究。首先报道并强调了掺杂的影响以及羟基和缺陷的位置。首先，考虑了具有不同手性（锯齿形和扶手椅）的石墨烯，并研究了 WF 对石墨烯宽度的依赖性。其次，计算了具有表面改性和缺陷的石墨烯的 WF。首先比较了羟基的不同分布，然后是不同位置缺陷的影响。第三，选择B、N、Al、Si和P作为掺杂元素，研究WFs的掺杂效果。

方法

所有计算均在基于密度泛函理论（DFT）[28]的 CASTEP 代码中进行，这是一种针对多电子系统电子结构的量子力学研究。 DFT 已广泛用于物理和化学性质的研究，包括石墨烯和碳纳米管的纳米材料 [29, 30]。 DFT还可以准确地模拟数十到数百个原子系统，将原子描述为量子粒子，即原子核和电子的集合[31]。

广义梯度近似（GGA）和局部密度近似（LDA）是量子力学计算中常用的交换相关函数。它们在方程式中描述。 (1)和(2)：

其中 R 我 和 r 分别是原子核和电子的坐标。不均匀电子气中的交换相关能被E代替 xc[ρ ] 在均匀电子气中。 GGA 和 LDA 都已用于二维材料的计算。勒贝格等人。发现使用 LDA 或 GGA 获得的二维材料的能带结构非常相似 [32]。同时Kharche和Gui的研究中使用GGA计算石墨烯的电性能，保证了精度[33, 34]。

至于 WF，之前基于扫描探针的研究表明，WF 的测量值为 4.6 eV，例如石墨 [35]。一般来说，4.6-4.9 eV 范围内的 WF 是可以接受的 [36, 37]。此外，LDA [38] 和 GGA [39] 分别预测 WF 为 4.48 和 4.49 eV。与实验数据相比，理论计算的 WF 略小。 GGA加入了非局部密度梯度，其非局部性更适合处理密度的不均匀性，而LDA在堆叠系统中效果更好。因此，在计算石墨烯的 WF 和电性能时，本理论研究选择了 GGA。此外，在此计算中，真空距离设置为 15 埃，这样板两侧之间的静电相互作用可以忽略不计，静电势达到其渐近值。超软赝势用于描述电子和离子之间的相互作用。截止能量为 340 eV，使用 9 × 9 × 1 Monkhorst–Pack k 点网格 [40] 对布里渊区进行采样，Methfessel–Paxton [41] 涂抹在 0.05 eV。自洽场能收敛准则为1.0 × 10 ^-6 eV，最大力为 0.03 eV/Å。

结果与讨论

不同尺寸之字形和扶手椅石墨烯的WF

一般而言，WF 可以定义为将电子从体中提取到无穷大所需的最小能量 [42]。在量子力学计算中，WF 被定义为真空能级 (V 0) 和费米能级 (E f)，如方程式所示。 (3):

晶体表面的 CASTEP 计算是在具有真空区域的平板上进行的。实际上，无限阵列的 2D 周期性材料板被宽真空间距隔开。 CASTEP 为此类系统产生费米能量和静电势的空间分布 [43]。不同宽度的石墨烯具有不同的特性。选择锯齿形和扶手椅具有不同手性的模型来阐明宽度对 WF 的影响。在此计算中，计算了具有 1 到 7 个单元格范围的样品。图 1 说明了锯齿形和扶手椅石墨烯的尺寸定义。锯齿形和扶手椅石墨烯的晶体取向不同；锯齿形石墨烯的晶体结构是菱形的，而扶手椅石墨烯的晶体结构是双斜的，如图 1a、b 所示。水平方向定义石墨烯的宽度，垂直方向定义石墨烯的长度。此外，一个晶胞被设置为一个碳环。

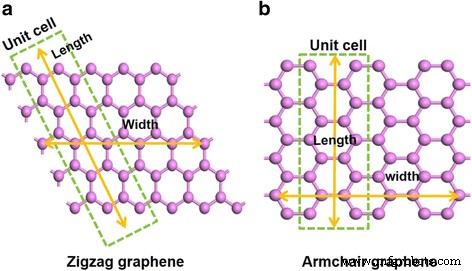
石墨烯尺寸的定义。之字形结构示意图（a ) 和扶手椅 (b ) 说明石墨烯尺寸定义的石墨烯。单元格被设置为绿色框中的碳环。黄色箭头代表宽度和长度方向

石墨烯带隙随着石墨烯宽度的变化而变化。一般来说，锯齿形石墨烯呈现金属特性，扶手椅石墨烯呈现半金属特性。然而，石墨烯中 WF 和宽度之间的关系是什么？图 2 显示了石墨烯尺寸和 WF 之间的关系。图 2a 中石墨烯的长度和宽度不相等，其中长度始终设置为七个单元，但宽度从一个单元到七个单元排列（1 × 7 到 7 × 7），而在图 2b 中，长度和宽度相等，其中大小从 2 × 2 个超级单元排列到 7 × 7 个超级单元。 WF 受石墨烯宽度的影响很大。通常，随着石墨烯尺寸的增加，WF 减小。此外，锯齿形石墨烯的 WF 总是大于扶手椅石墨烯的 WF。我们认为这种现象是由石墨烯的晶体结构引起的。实际上，晶体取向对材料的性能有很大影响。锯齿形石墨烯的晶体结构为立方体结构，而扶手椅石墨烯的晶体结构为菱形结构。通过比较图 2a、b 之间的 WF，宽度和长度不等的石墨烯（图 2a 中的石墨烯）的 WF 将大于宽度和长度不等的石墨烯（图 2b 中的石墨烯）的 WF和长度。图 1a 中 WF 的减少梯度也更大。此外，扶手椅和锯齿形石墨烯中的 6 × 6 和 7 × 7 超级晶胞之间的 WF 差异很小；我们相信当石墨烯尺寸达到6 × 6个超级晶胞时，WF将保持稳定。

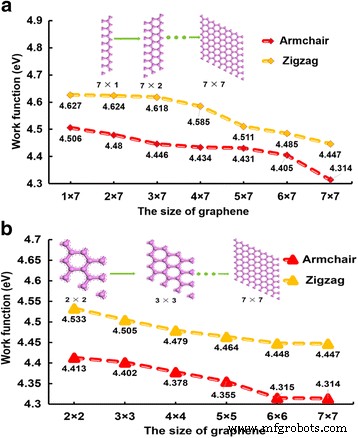
石墨烯尺寸与WF的关系。石墨烯尺寸与WF的关系。石墨烯的长宽在(a )，而 (b )

还对不同宽度的石墨烯的带隙进行了分析，如表 1 所示。一般而言，小尺寸的石墨烯的带隙也较小。然而，随着宽度的增加，带隙减小甚至关闭[44]。儿子等。已经表明，具有均匀扶手椅或锯齿形边缘的石墨烯纳米带都具有能隙，这些能隙随着系统宽度的增加而减小 [45]。表 1 还显示带隙随着石墨烯尺寸的增加而减小。总体而言，扶手椅石墨烯的带隙小于锯齿形石墨烯的带隙。宽度和长度不等的石墨烯也比宽度和长度不等的石墨烯具有更大的带隙。

<图>

羟基、缺陷以及羟基和缺陷的位置对 WF 的影响

功能化一直是设计和提高目标材料性能的一种改性方法；羟基化是这些方法之一。分析了羟基和缺陷的数量和位置对 WF 的影响，如图 3 所示。插图（a）和（b）分别说明了石墨烯中羟基和缺陷位置的结构图。在该计算中，选择了具有 4 × 4-超胞尺寸的原始锯齿形石墨烯，计算出的 WF 为 4.479 eV，略小于实验结果 [12]。羟基改性会导致 WF 增加。康等人。通过实验确定氧化物石墨烯的 WF 值为 4.91 eV [27]。然而，没有报道官能团的数量和它们的位置。我们计算出的具有一个羟基的锯齿形石墨烯的 WF 为 4.504 eV，大于原始锯齿形石墨烯的 WF。随着羟基的增加，WF 增加。而且，增量比较大；最大 WF 达到 5.102 eV。这一结果是由于羟基效应，随着羟基数量的增加，这种效应更加突出。此外，选择四个羟基来分析官能团分布对 WF 的影响。插图 (a) 给出了四种不同的羟基分布方式；分布是对称的。分布密集，WF大。但是，由于分布分散，WF 很小。 WF 的最大值为 4.829 eV，而 WF 的最小值为 4.658 eV。这种现象应该是由羟基的聚集效应引起的。此外，研究了 4 × 4 石墨烯中的四个不同缺陷位点，如插图 (b) 所示。一般来说，缺陷会导致石墨烯 WF 的减少。裴等人。表明当空位存在时，石墨烯 WF 较小。并且缺陷率越小，WF 变得越小[46]。缺陷在中心的石墨烯的 WF 为 4.337 eV，而缺陷偏离中心的石墨烯的 WF 较大，为 4.363 eV，略小于 4 × 4 原始锯齿形石墨烯的 WF。这种差异意味着中心的缺陷对结构的影响更大，因此 WF 最小。因此，我们建议中心缺陷位点对 WF 有很大影响，而偏离中心的缺陷影响较小。金等人。发现空穴掺杂导致 WF 的差异高达 400 meV，这与我们计算的结果一致 [47]。

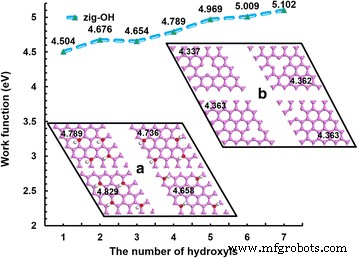
WF 与羟基数之间的关系。 WF与羟基数的关系；石墨烯的大小设置为 4 × 4 个超级单元。插图展示了四种不同的羟基分布模式（a ) 和缺陷 (b )

B、N、Al、Si、P 掺杂对 WF 的影响

掺杂是控制 WF、带隙和吸附性能的有效方法。因此，在本研究中研究了掺杂效应和浓度。图 4 显示了不同掺杂剂对 WF 的影响；石墨烯的大小为 4 × 4 个超级单元。来自 1、2、3、4、5 和 6 个原子的掺杂剂分别响应 2.4、4.9、7.3、9.8、12.2 和 14.6% 的浓度。掺杂剂对WF的影响是显着的，并有一定的趋势。首先，除了 B 掺杂的石墨烯外，所有掺杂的石墨烯的 WF 都随着浓度的增加而降低，显示出相反的效果。 Legesse 等人。还发现碱金属掺杂石墨烯的 WF 随着浓度的增加而降低 [48]。其次，B 和 Al 掺杂石墨烯中 WF 的增量相对大于其他石墨烯。通过比较 WF 值，掺杂 B 和 Al 的 p 型石墨烯具有更大的 WF，其中 B 掺杂石墨烯浓度为 14.6% 时的最大值高达 5.148 eV。相比之下，掺杂有 N 和 P 的 n 型石墨烯的 WF 小得多；在 P 掺杂的石墨烯中浓度为 14.6% 时，最小值降低到 3.23 eV。权等人。还表明 p 掺杂剂会将石墨烯 WF 从 4.2 eV 增加到 5.14 eV [49]。克瓦什宁等人。还证明了 B 掺杂会导致 WF 增加的现象，但 N 和 P 掺杂导致 WF 减少 [19, 50]。此外，Si 掺杂石墨烯的 WF 相对稳定。这可能是因为 C 和 Si 原子是同系物。因此，我们建议 p 型掺杂会导致 WF 增加；然而，数量是由掺杂元素决定的。 WF 在 14.6% 的浓度下趋于稳定。另一方面，n型掺杂会使WF急剧下降。

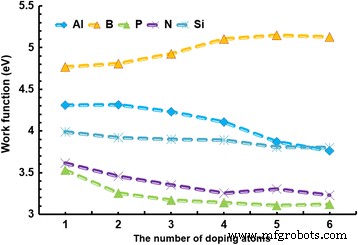
WF 与掺杂原子数的关系。 WF 与掺杂原子数的关系。石墨烯中掺杂了Al、B、P、N和Si等不同类型的掺杂剂，大小为4 × 4个单元

虽然已经分析了掺杂剂对WF的影响，对石墨烯的应用具有重要意义，但对各种原子进行掺杂的可行性是不同的。因此，我们计算了 GNR 中不同掺杂原子的形成能。形成能 [51] 被描述为方程。 (4):

$$ {E}_{\mathrm{formation}}={E}_{\left(\mathrm{GNRs}+d\right)}+{nE}_{\mathrm{C}}-{E}_ {\left(\mathrm{GNRs}\right)}-{nE}_{\mathrm{d}} $$ (4)

其中 E 形成是形成能，E (GNRs) 是原始 GNRs 的能量，E （GNR + d ) 是掺杂 GNR 的能量，d 是掺杂原子，n 是数字，E C 和 E d 是碳原子和掺杂原子的化学势。

形成能可以用来评价用原子掺杂的可行性是否好。形成能越小，掺杂越容易。图5显示掺杂Al的石墨烯具有最大但最不稳定的形成能； Al原子的增加导致4 × 4-单元尺寸的石墨烯结构发生剧烈变化。相比之下，B和N的形成能很小，但随着原子数的增加，变化很小。与B和N原子相比，Al、Si和P原子的形成能波动更大。这是因为石墨烯中Al、Si和P的形成能较大，这意味着Al-、Si - 和P掺杂的石墨烯稳定性较差，尤其是Al掺杂的石墨烯结构最不稳定。它们相对难以掺杂在石墨烯中。总的来说，石墨烯中的 Al 掺杂是困难的，而 B 和 N 的掺杂更容易。这些掺杂剂在​​石墨烯中的 WF 和形成能记录在表 2 中。

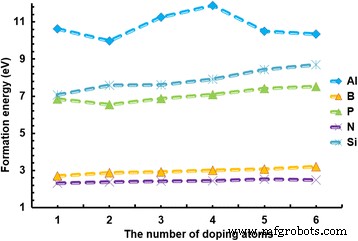
形成能与掺杂原子数的关系。形成能与掺杂原子数的关系。不同类型的掺杂原子，例如 Al、B​​、P、N 和 Si，以 4 × 4 单元尺寸掺杂在石墨烯中

<图>

结论

本研究研究了石墨烯在不同状态下的 WF，如表面改性、掺杂和缺陷。基本上，随着石墨烯宽度的增加，WF 会减少。对于羟基改性，当羟基数目增加时，WF 较大。此外，当羟基分布密集时，WF 也增加。该缺陷会降低石墨烯 WF，这与位置无关。 B和Al的p型掺杂会导致WF增加；然而，增加的量是由掺杂剂决定的。 N和P的n型掺杂大大降低了WF。这些发现将为控制石墨烯和进一步改进石墨烯基器件的设计提供理论支持。