不同旋转角度外壳中TiO2-水纳米流体稳定性和自然对流的实验研究

背景

自制备纳米流体以来，由于其优良的导热性能[1,2,3]，纳米流体被广泛应用于传热领域[4,5,6]，尤其是自然对流领域[7,8,9]。

许多研究人员对纳米流体的自然对流换热特性进行了数值研究。他等人。 [10, 11]分别应用单相和两相晶格玻尔兹曼方法数值研究了方腔中Al2O3-水纳米流体的自然对流换热。 Sheikholeslami 等。 [12]通过格子Boltzmann模拟方法研究了内三角圆柱体填充Al2O3-水纳米流体的水平圆柱外壳的磁流体动力自然对流热传递特性。乌丁等人。 [13] 基于 Darcy-Forchheimer 模型研究了各种纳米流体沿着嵌入多孔介质的垂直板的自然对流热传递。孟等人。 [14] 数值研究了填充有 Al2O3-水纳米流体的水平圆柱体的自然对流。艾哈迈德等人。 [15]使用两相晶格玻尔兹曼方法研究了倾斜外壳中CuO-水纳米流体的自然对流。齐等人。 [16]数值模拟了封闭空间内Cu-Ga纳米流体的自然对流。

除了以上对纳米流体自然对流的数值模拟之外，越来越多的研究人员对纳米流体的自然对流进行实验研究。李等人。 [17] 通过实验研究了 ZnO-EG/水纳米流体的自然对流传热。胡等人。 [18, 19] 实验研究了分别填充有 TiO2-水和 Al2O3-水纳米流体的方形外壳的自然对流换热增强。何等人。 [20] 实验研究了不同尺寸的垂直方形外壳的自然对流热传递，其中填充了 Al2O3-水纳米流体。赫里斯等人。 [21, 22, 23] 分别实验研究了不同种类纳米流体（Cu/水、Al2O3-水和CuO-水）在圆管中的对流传热特性。曼苏尔等人。 [24] 通过实验研究了填充有 Al2O3-水纳米流体的斜管的混合对流。张等人。 [25] 通过实验研究了 Al2O3-水纳米流体在薄外壳中的自然对流。文等人。 [26, 27] 分别实验研究了Al2O3-水纳米流体和TiO2-水纳米流体在层流条件下的对流传热特性。宣等人。 [28] 实验研究了铜-水纳米流体在黄铜直管中的对流换热。

以上文献对纳米流体的自然对流换热特性做出了巨大贡献。然而，需要进一步研究填充纳米流体的具有不同旋转角度的外壳的自然对流换热增强。因此，TiO2-水纳米流体在不同旋转角度（α =−45°, α =0°，α =45°，并且 α =90°) 在本文中进行了实验研究。

方法

纳米流体的制备及其稳定性

选择 TiO2 作为纳米颗粒。图 1 显示了 TiO2 纳米颗粒在不同放大倍数下的 SEM、TEM 和 XRD 图像。从SEM图像可以发现纳米颗粒很容易聚集在一起，需要采取一些措施来制备稳定的纳米流体。从TEM图像还可以发现，粒径约为10nm左右，纳米颗粒的形状是扁平的。在相同质量分数下，扁平纳米颗粒比球形纳米颗粒具有更大的传热面积，有利于增强传热。图 1g 显示了 TTP-A10 TiO2 纳米颗粒的 XRD 谱。正如所观察到的，强而尖锐的峰表明 TTP-A10 TiO2 纳米颗粒样品是高度结晶的。样品的平均粒径可以通过方程 1 中的 Scherrer 方程计算。 (1).由这些衍射峰值（111、200、021、202和311）计算得到的TiO2纳米颗粒尺寸分别为6、9、14、20和35nm，根据衍射，最小的纳米颗粒尺寸约为6和9nm峰值（111 和 200）。大的纳米颗粒尺寸可能是由纳米颗粒的聚集引起的。最小值（6 和 9 nm）可能是纳米颗粒的真实尺寸，少数纳米颗粒的尺寸可能是 6 nm，而大多数纳米颗粒的尺寸可能在 9 nm 左右，这更接近于制造商提供的描述（ 10 nm) 和 TEM 图像 (10 nm).

其中 k 是形状因子的值，k =0.9； λ 是 X 射线波长；和 β 是以弧度为单位的峰高半峰全宽 (FWHM) 加宽的线，θ 是布拉格衍射角。

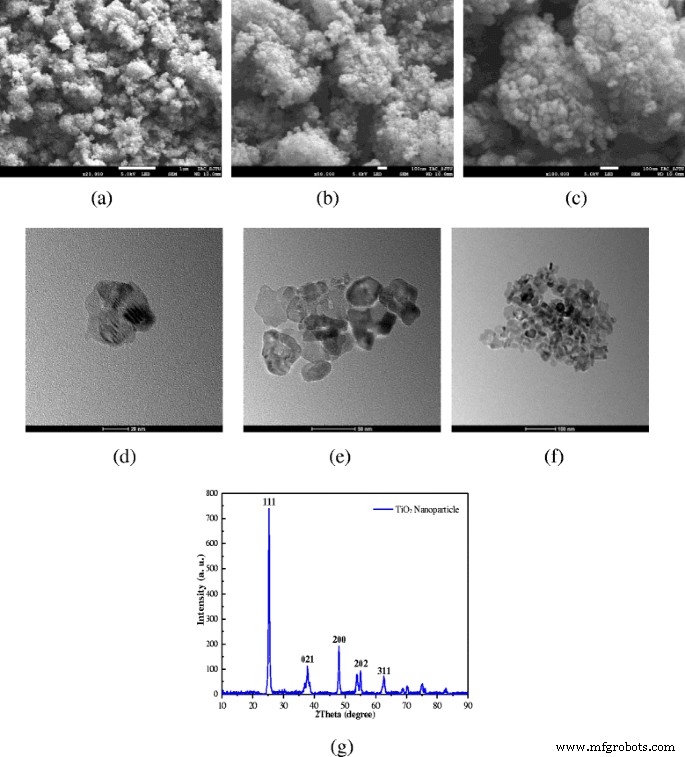
纳米粒子的形态。不同放大倍数下 TiO2 纳米颗粒的 SEM、TEM 和 XRD 图像。 一 SEM × 20000。b SEM × 50000。c SEM × 100000。d 透射电镜 20 纳米。 e 透射电镜 50 纳米。 f 透射电镜 100 纳米。 g XRD

采用两步法制备不同纳米粒子质量分数（wt% =0.1%、wt% =0.3%、wt% =0.5%）的TiO2-水纳米流体，如图2所示。机械搅拌时间为每个子步骤半小时，超声时间为 40 分钟。表1显示了纳米流体制备中一些材料和设备的信息。图 3 显示了铺设前和铺设 72 小时后的 TiO2-水纳米流体。可以看出，试管中纳米颗粒几乎没有沉积，本文制备的纳米流体表现出良好的稳定性。

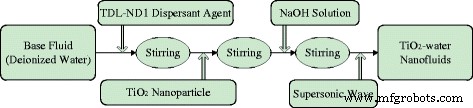
纳米流体的制备。 TiO2-水纳米流体的两步法制备工艺

TiO2-水纳米流体的稳定性观察。不同时间的TiO2-水纳米流体。 一 铺设前。 b 72小时后

除了研究试管内是否有纳米颗粒沉积外，透光率（τ ) 纳米流体对其稳定性的影响也进行了讨论。图 4 给出了透射率 (τ ) TiO2-水纳米流体 (wt% =0.5%) 随不同 pH 值和剂量 (m ) 的分散剂。通过紫外可见分光光度计(UV-1800(PC))测量透射率。众所周知，如果纳米粒子在水中均匀分布，则纳米粒子反射的光最多，反射率高（透射率低）。因此，纳米流体的稳定性与透射率成反比，稳定的纳米流体具有较低的透射率。从图 4 可以看出，具有 m 的纳米流体 =6wt%和pH =8的透光率最低，稳定性最好。本实验中不同纳米颗粒质量分数的纳米流体在m制备 =6 wt%，pH =8，可以保证纳米流体的稳定性。

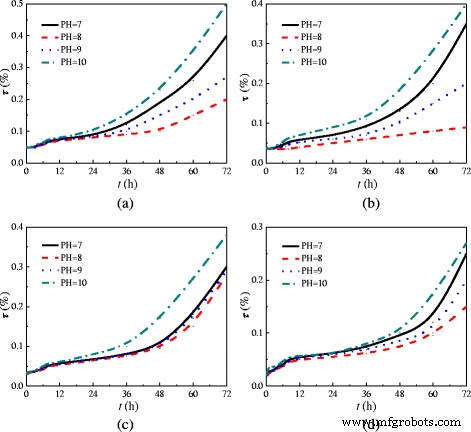
TiO2-水纳米流体的透射率。透射率 (τ ) TiO2-水纳米流体 (wt% =0.5%) 在不同 pH 值下随时间 (h ) 在不同的剂量 (m ) 的分散剂。 一 米 =5wt%。 b 米 =6wt%。 c 米 =7wt%。 d 米 =8 wt%

实验系统

图5显示了三个实验组的示意图。三个矩形围栏的尺寸分别为10厘米（宽） × 20厘米（高）、5厘米（宽） × 20厘米（高）、20厘米（宽） × 20厘米（高）。宽度和高度定义为 W 和 H , 和纵横比 (A ) 的外壳定义为 A =W /H .外壳的左壁（铜板）由连接到直流电源的硅胶加热片加热。外壳的右壁（铜板）由连接恒温水浴的小腔（材质也是铜）内的冷却水冷却。外壳两侧的温度由连接到数据采集仪器 (Agilent 34972A) 的六个热电偶获得。外保温层用于防止热量散失。

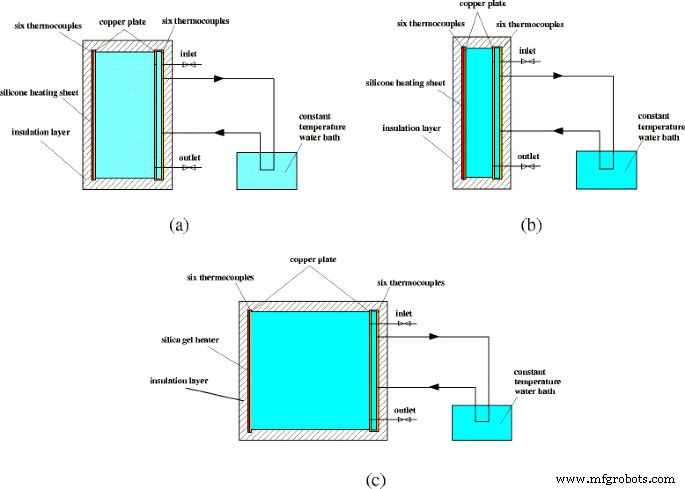
实验装置示意图。三种不同纵横比实验组示意图。 一 A =1:2。 b A =1:4。 c A =1:1

两种不同旋转角度(α =−45°, α =0°，α =45°，并且 α =90°) 填充 TiO2-水纳米流体在本文中进行了研究。对于带有 α 的外壳 =−90°，顶壁为热壁，底壁为冷壁，外壳内的传热主要是热传导。然而，手稿主要研究了外壳中纳米流体的自然对流热传递，因此，带有 α 的外壳 =−90° 不在本手稿中考虑。图6所示为不同旋转角度的外壳示意图。

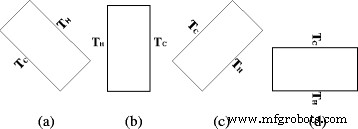
旋转角度示意图。具有四种不同旋转角度的外壳示意图。 一 α =−45°。 b α =0°。 c α =45°。 d α =90°

数据处理

力量Q 硅胶发热片提供如下：

其中 U 和我 分别为直流电源的电压和电量。

有效功率Q 网如下：

其中 Q loss是热流计测得的热量损失。

硅胶发热片旁边的铜板侧温度\( {T}_{\mathrm{H}}^{*} \)如下：

其中 T 1、T 2, ..., T 6是热电偶的温度。

纳米流体T旁边的铜板侧（外壳左侧）的温度 H如下：

其中 δ =0.005m为铜板厚度，A 是铜板的面积，λ w 是铜板的导热系数。

绝缘层旁边的铜板侧（外壳右侧）温度T C ^∗ 如下：

其中 T 7、T 8, ..., T 12为外壳右侧热电偶温度。

当达到热平衡状态时，冷却水的温度与靠近冷却水的铜板一侧的温度相同。纳米流体T旁边的铜板侧（外壳右侧）的温度 C可以计算如下：

定性温度T m 定义如下：

对流传热系数h 如下：

努塞尔数定义如下：

其中 λ f为外壳内流体的热导率。

不确定性分析

对流传热系数的误差传递公式如下[19]：

Nusselt数的误差传递公式如下[19]：

基于方程。 (10)和(11)，本实验对流传热系数和努塞尔数的误差分别为5.65%和6.34%。可以发现，实验集的误差较小，可以保证实验结果的可靠性和准确性。

结果和讨论

实验验证

在研究纳米流体之前，需要进行实验验证。图7 水的实验结果与文献发表的A围栏结果对比图 =1:2, A =1:4，并且 A =1:1。 A 机箱的最大误差 =1:2, A =1:4，并且 A =1:1 分别为 8.4、9.5 和 8.1%。可以发现，实验结果与已发表文献[20, 29]的结果具有较好的一致性，验证了实验系统的准确性和可靠性。

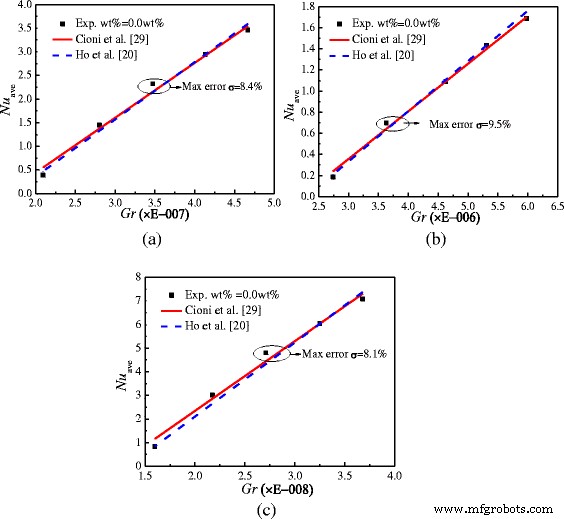
实验集验证。在具有两种不同纵横比的外壳中，实验结果与已发表文献之间的努塞尔数比较。 一 A =1:2。 b A =1:4。 c A =1:1

带有 A 的外壳 =1:2

本文讨论了旋转角度对TiO2-水纳米流体自然对流传热特性的影响。图 8 表示平均 Nusselt 数随带有 A 的围栏旋转角度的变化 =1:2。由图 8 可以看出，随着旋转角度的增加，努塞尔数先增大后减小。旋转角α的外壳 =0° 具有最高的努塞尔数，其次是具有旋转角度 α 的外壳 =45° 和 α =90°，旋转角度α的外壳 =−45° 具有最低的努塞尔数。当旋转角度减小时（α ≤ −90°)，当旋转角度减小到α时，传热几乎是热传导 =−90°。当热壁位于外壳顶部，冷壁位于外壳底部时（α =−90°)，浮力方向向上，但顶壁阻止流体向上移动。纳米流体在外壳内的运动很小，主要的传热是热传导，因此努塞尔数很小。带有 α 的外壳 =−45° 与 α 更接近外壳 =−90° 并显示与其他旋转角度相比最小的努塞尔数。对于旋转角度α的外壳 =45° 和 α =90°，靠近底部热壁的流体被加热向上移动，靠近顶部冷壁的流体被冷却向下移动。热流体和冷流体的方向相反，阻止了自然对流热传递，导致与α的外壳相比，努塞尔数较低 =0° 但与具有 α 的围栏相比，努塞尔数更高 =−45°。还可以看出，各种旋转角度之间的差异随着加热功率的增加而增加。这是因为在低加热功率下，旋转角度的影响对传热起主要作用，对流对传热的影响很小。然而，对流换热强度随着加热功率的增加而增加，并且在高加热功率下对传热起主要作用，导致高加热功率下与低加热功率下的各种旋转角度之间的差异更大。

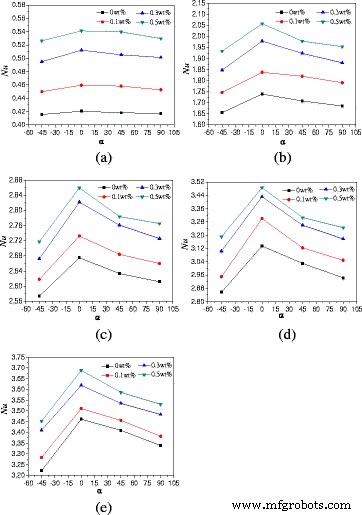
努塞尔数随旋转角度的变化 (A =1:2)。纳米流体的平均努塞尔数随外壳旋转角度的变化 (A =1:2) 在不同的加热功率下。 一 问 =1 W。b 问 =5 W。c 问 =10 瓦。d 问 =15 W。e 问 =20 W

除了旋转角度外，还讨论了纳米粒子质量分数对自然对流传热的影响。图 9 显示了平均努塞尔数随纳米颗粒质量分数的变化。可以发现，努塞尔数随着纳米粒子质量分数的增加而增加。对于加热功率Q =1 W 和 α =0°，与水相比，具有wt% =0.1%、wt% =0.3%和wt% =0.5%的TiO2-水纳米流体可以分别提高9.3、21.8和28.7%的传热。增强率随着加热功率的增加而减小。对于加热功率Q =20 W 和 α =0°，与水相比，具有wt% =0.1%、wt% =0.3%和wt% =0.5%的TiO2-水纳米流体可以分别提高传热1.4、4.6和6.6%。在高加热功率下湍流强度起主要作用，纳米颗粒质量分数对传热的影响变小。

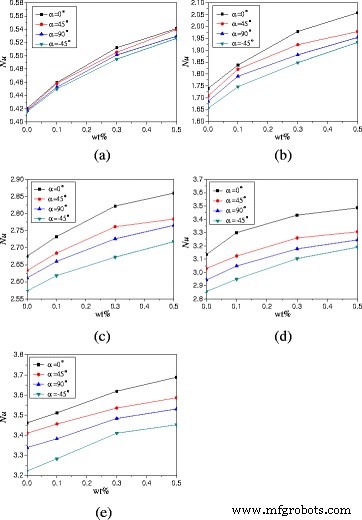
Nusselt 数随纳米粒子质量分数的变化 (A =1:2)。外壳中纳米流体的平均努塞尔数变化 (A =1:2) 不同加热功率下的纳米颗粒质量分数。 一 问 =1 W。b 问 =5 W。c 问 =10 瓦。d 问 =15 W。e 问 =20 W

本文研究了加热功率对自然对流传热的影响。图 10 显示了平均努塞尔数随加热功率的变化。对于 α =0°，Q处的TiO2-水纳米流体 =5 瓦，Q =10 瓦，Q =15 W，和 Q 与 Q 相比，=20 W 可以将传热提高 280.2、428.4、544.1 和 581.5% =1 W。高加热功率增强了湍流强度并改善了传热。

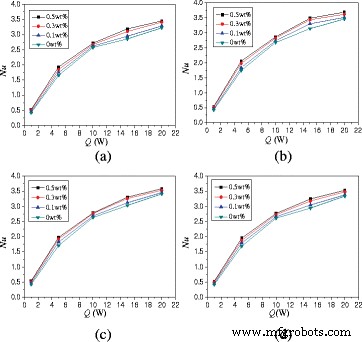
努塞尔数随加热功率的变化 (A =1:2)。外壳中纳米流体的平均努塞尔数变化 (A =1:2) 不同旋转角度下的加热功率。 一 α =−45°。 b α =0°。 c α =45°。 d α =90°

带有 A 的外壳 =1:4

为了研究围墙长宽比对传热的影响，采用A围墙的自然对流换热特性 =1:4填充TiO2-水纳米流体进行了研究。图 11 给出了平均 Nusselt 数随外壳旋转角度的变化。可以得到类似A的结论 =1:2 说明 Nusselt 数随着旋转角度的增加先增大后减小。以wt% =0.5%的纳米流体为例，A之间的差异 =1:4 和 A =1:2 是外壳中努塞尔数的增强率（从 6.5% 到 20.7%）（A =1:4，α =0°) 与外壳中的 (A =1:4，α =−45°) 高于围护结构中 Nusselt 数 (A =1:2，α =0°) 与外壳中的 (A =1:2，α =−45°).

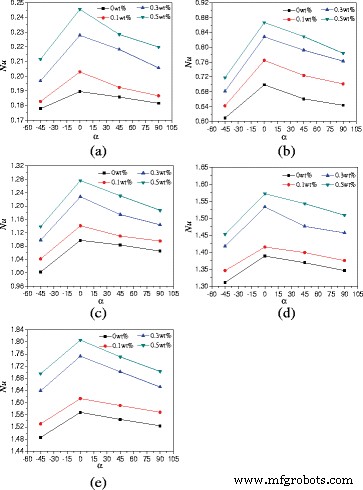
努塞尔数随旋转角度的变化 (A =1:4)。纳米流体的平均努塞尔数随外壳旋转角度的变化 (A =1:4) 在不同的加热功率下。 一 问 =1 W。b 问 =5 W。c 问 =10 瓦。d 问 =15 W。e 问 =20 W

图 12 显示了平均努塞尔数随纳米颗粒质量分数的变化。对于加热功率Q =1 W 和 α =0°，与水相比，具有wt% =0.1%、wt% =0.3%和wt% =0.5%的TiO2-水纳米流体可以分别提高7.1、20.2和29.5%的传热。增强率随着加热功率的增加而减小。对于加热功率Q =20 W 和 α =0°，TiO2-水纳米流体与水相比，wt% =0.1%、wt% =0.3%和wt% =0.5%可以分别提高传热2.9、11.8和15.1%。

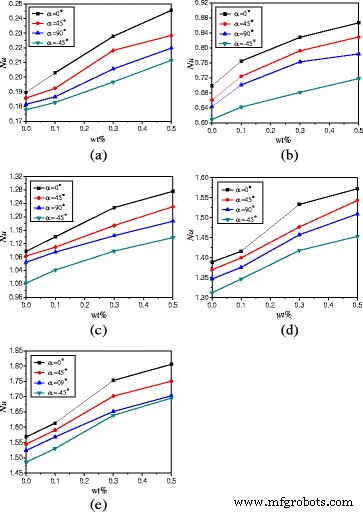
Nusselt 数随纳米粒子质量分数的变化 (A =1:4)。外壳中纳米流体的平均努塞尔数变化 (A =1:4) 不同加热功率下的纳米颗粒质量分数。 一 问 =1 W。b 问 =5 W。c 问 =10 瓦。d 问 =15 W。e 问 =20 W

图 13 显示了平均努塞尔数随加热功率的变化。与加热功率 Q =1 W 的水相比，纳米流体的平均努塞尔数可以提高 242.4% ~ 701.5%。对于 α =0°，TiO2-水纳米流体，在 Q 下，wt% =0.5% =5 瓦，Q =10 瓦，Q =15 W，和 Q =20 W 与 Q 相比，可以将传热提高 253.0、419.9、540.3 和 635.6% =1 W，分别。

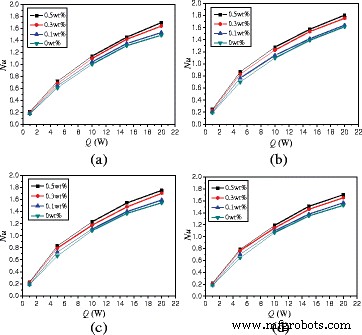
努塞尔数随加热功率的变化 (A =1:4)。外壳中纳米流体的平均努塞尔数变化 (A =1:4) 不同旋转角度下的加热功率。 一 α =−45°。 b α =0°。 c α =45°。 d α =90°

A 之间的比较 =1:2, A =1:4，并且 A =1:1

由于本文篇幅所限，A包围的结果 =1:1 仅在图 14 中给出，不同旋转角度、纳米粒子质量分数和加热功率对传热的影响都可以在图 14 中显示。 A =1:2, A =1:4，并且 A =1:1，图14显示了A之间平均努塞尔数的比较 =1:2, A =1:4，并且 A =1:1 在不同的旋转角度。发现努塞尔数随着外壳纵横比的增加而增加。围栏的努塞尔数 (A =1:1 和 A =1:2) 与围栏的 Nusselt 数 (A =1:4) 分别在相同条件下。对于Q =1 W 和 α =0° 示例，纳米流体重量％ =0.5％，重量％ =0.3％，重量％ =0.1％，重量％ =0.0％在具有A的外壳中 =1:2 与具有A的外壳相比，可以提高120.4、124.9、126.5和121.9%的热传递 =1:4。增强率随着加热功率的增加而减小。 vFor Q =20 W 和 α =0°，纳米流体在带有 A 的外壳中，wt% =0.5%，wt% =0.3%，wt% =0.1%，wt% =0.0% =1:2与A =1:4的外壳相比，可以提高104.2、106.5、117.6、120.7%的热传递。还发现努塞尔数从wt% =0.1%增加到wt% =0.3%大于从wt% =0.3%到wt% =0.5%。这是因为热导率的增加在传热过程中起主要作用，从wt% =0.1% 到wt% =0.3%，导致了很大的增强。但粘度的增加开始在传热中起主要作用，从wt% =0.3%到wt% =0.5%，这引起了很小的增强。由于图14可以覆盖所有的实验结果，图14的详细结果如表2、3、4所示。

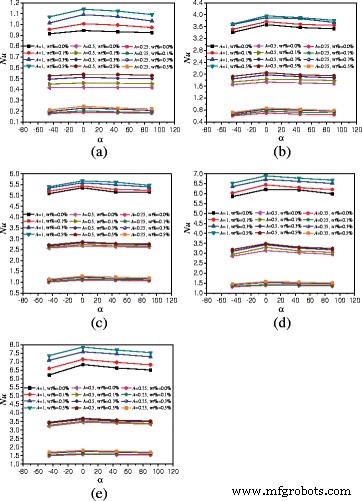
不同纵横比之间的努塞尔数比较。不同纵横比(A)纳米流体的平均努塞尔数比较 =1:1, A =1:2，A =1:4) 和不同加热功率下的旋转角外壳。 一 问 =1 W。b 问 =5 W。c 问 =10 瓦。d 问 =15 W。e 问 =20 W

结论

The stability and natural convection heat transfer characteristics of the two enclosures with different rotation angles (α  = −45°, α  = 0°, α  = 45°, and α  = 90°) filled with TiO2-water nanofluid are experimentally investigated. Some conclusions are obtained as follows:

1. (1)

   TiO2-water nanofluid with m  = 6 wt% and pH = 8 has the lowest transmittance and has the best stability.

2. (2)

   The enclosure with rotation angle α  = 0° has the highest Nusselt number followed by the enclosure with rotation angles α  = 45° and α  = 90°; the enclosure with rotation angle α  = −45° has the lowest Nusselt number.

3. (3)

   There is a higher heat transfer performance in a bigger aspect ratio enclosure. The Nusselt numbers of enclosure (A  = 1:1 and A  = 1:2) can be enhanced by 190.6% ~ 224.4% and 103.6% ~ 172.0% compared with the Nusselt numbers of enclosure (A  = 1:4) at the same conditions.

4. (4)

   Nusselt numbers increase with nanoparticle mass fractions, but the enhancement ratio decreases with the heating power.

5. (5)

   Average Nusselt numbers increase with the heating power. Average Nusselt numbers of nanofluid can be enhanced by 701.5% compared with water at the best.