平带材料的计算设计

背景

材料的电学和磁学性质主要由它们的能量色散决定。例如，当价/导带具有大的能量色散时，电子电导率高。当能带色散很小时会产生磁性。通常，能带色散是由原子波函数的特性决定的。因此，大多数磁性化合物都含有磁性元素，如过渡金属元素和稀土元素。如果能合成一种不含磁性元素的磁性材料，其影响是不可估量的。

在本文中，我们通过第一性原理计算提出了这种不含磁性元素的铁磁体候选物。非磁性原子的轨道组成的带宽通常很小，但在某些情况下，其带宽变得非常小。这个窄带称为平带，如果费米能级正好在这个平带上，就有可能取铁磁基态。平带物理的研究有很多，综述见综述[1, 2]。

在本文中，我们简要介绍了平带。首先，我们考虑一个简单的紧束缚（TB）哈密顿量 \( {H}_0=\varepsilon \sum \limits_i{c}_i^{+}{c}_i+\sum \limits_{i,j}{t }_{ij}{c}_i^{+}{c}_j \) (1), 其中 c 我 表示 i 上的湮灭算子 -站点，ε 是现场能量，跳跃积分t ij 是有限且各向同性的 (=t ) 仅当站点 i 和 j 在最近的邻居中。量子力学表明，在大多数情况下，大的跳跃积分会产生大的能量色散。例如，如果 H 0 定义在一个简单的方格上，得到的能量色散为 E (k ) =ε + 2t (cosk x + cosk y)。带宽W =8t , 与 t 成正比 .由于 t 由类原子波函数的重叠决定，如果带由 s 或 p 轨道组成，则它成为宽带。在这种情况下，由于自旋对齐状态失去了很大的动能，因此不期望磁基态。

然而，在一些特定的格子上，这个简单的关系 W ~ t 不成立。例如，如果 H 0 定义在烧绿石晶格上，出现双重退化的无色散带。烧绿石晶格被定义为烧绿石结构的 A 位子晶格，见图 1。我们可以从数学上证明这种平坦带的出现，例如，参见参考文献 [3]。除了烧绿石晶格之外，还有几种晶格会产生平带，例如，2D 棋盘格、2D Kagome 晶格等 [1, 2]。有趣的是，我们可以证明如果这个平带是半填充的，那么系统对于任何都具有唯一的铁磁基态 原子内库仑相互作用的正值 U [4]。这种导出平带的晶格在局域自旋系统中称为“几何受挫晶格”。事实上，一系列烧绿石氧化物 R2Ti2O7（R：稀土元素）具有各种新颖的磁性，如量子自旋液体、自旋冰和磁单极子 [5,6,7,8,9]。最近，在受挫的二聚体磁铁 Ba2CoSi2O6Cl2 [10] 中发现了几乎完美的挫败感。已经构建了该化合物的有效理论，该理论可以解释强磁场中奇怪的磁性[11]。

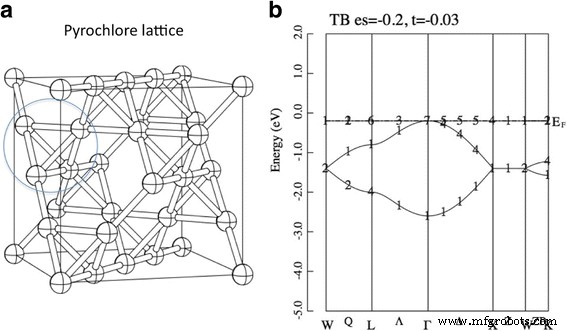
一 烧绿石晶格。球和棒分别表示位点和键。这是 A2B2O7 烧绿石结构的 A 位亚晶格。 b 烧绿石晶格上的紧束缚模型（方程 1）的谱带色散。参数设置为ε =− 0.2 和 t =- 0.03。能量单位是eV。 (b 中的数字 ) 表示不可约表示的索引，参见参考。 [34]

除了铁磁基态之外，理论上还表明平带会引起一些有趣的特性，例如超导性、量子霍尔效应和各种拓扑状态 [12,13,14]。因此，找到一种实际上具有平坦带的化合物非常重要。有几种理论尝试使用光刻 [15] 或光子晶格 [16] 来实现平带。除了这些细观材料，我们注意到精心设计的二维铟-亚苯基有机金属框架 (IPOF) 显示出极好的平坦带 [17]。有趣的是，这个平带在拓扑上是非平凡的，可以作为高温分数量子霍尔效应的舞台。尽管进行了这些积极的研究，但尚未实现预期的磁性长程有序，可能是因为这些尝试仅限于 2D 系统。另一项有趣的研究表明，吸附在石墨烯上的有机分子会产生长程磁序[18]。然而，这种磁序的微观起源尚不清楚。

如上所述，为了使铁磁性出现在这个平带上，需要在这个平带上调整费米能级。在大多数烧绿石氧化物 A2B2O7 中，费米能级位于由 B 位轨道组成的带上。但是，由于必须在 A 位亚晶格（烧绿石晶格）上形成平带，因此 B 位离子是惰性的。此外，由于跳跃积分需要是各向同性的，所以费米能级必须在A位的s轨道上。

结合上述条件，我们可以选择在价带顶部具有平坦带的烧绿石氧化物候选物：

由于价带顶部具有 A-s 特征，A 位离子通常为 (a) Tl ¹⁺ ; (b) Sn ²⁺ , Pb ²⁺ ; (c) Bi ³⁺ .所有这些离子都具有 (5s) ² 或 (6s) ² 配置。 B位必须是惰性的，所以我们可以选择（a）Mo ⁶⁺ , W ⁶⁺ ; (b) 铌 ⁵⁺ , Ta ⁵⁺ ; (c) Ti ⁴⁺ , Sn ⁴⁺ .所有这些 B 位离子都有封闭的壳层，即 (n d) ⁰ 或 (n p) ⁰ 配置其中 n =3、4、5。

在以上组合中，我们重点关注三个化合物：

化合物 (b) Sn2Nb2O7 和 (c) Bi2Ti2O7 已经合成 [19,20,21,22,23]，而 (a) Tl2Mo2O7 尚未报道。然而，已经合成了一种类似的烧绿石氧化物 Tl2Ru2O7，并显示出独特的金属-绝缘体转变 [24]。由于 Mo 和 Ru 的原子半径相似，我们预计在一定条件下可以合成 Tl2Mo2O7。有趣的是，已知 (b) Sn2Nb2O7 和 (c) Bi2Ti2O7 都是光催化材料的候选者。

我们已经对这些化合物进行了第一性原理计算。本文组织如下：在“方法”部分，描述了计算方法和我们计算的晶体结构。在“结果和讨论”部分，我们展示了计算结果并进行了一些讨论。 “结论”部分描述了摘要。

方法

我们已经根据第一性原理计算了 Tl2Mo2O7、Sn2Nb2O7 和 Bi2Ti2O7 的电子结构。为简单起见，我们假设它们都具有理想的 A2B2O6O'烧绿石结构。由于有两个氧位，所以我们称它们为O和O'以区别它们。我们使用了全电位增强平面波 (FLAPW) 方案，交换相关电位是在一般梯度近似内构建的 [25]。我们使用了计算机程序 WIEN2k 包 [26]。参数RK 最大值被选为 7.0。 k 采用点网格，使得第一布里渊区的网格总数为~ 1000。我们还优化了晶体结构，固定了空间群对称性。 A2B2O6O'的晶体结构如下：空间群Fd-3m (#227), A (0,0,0), B (1/2,1/2,1/2), O (x ,0,0) 和 O' (1/8,1/8,1/8)。对于 Sn2Nb2O7 和 Bi2Ti2O7，我们使用了实验晶格参数。对于 Tl2Mo2O7，我们还优化了晶格参数 (a ) 并获得 a =10.517 Å，这与类似化合物 Tl2Ru2O7 的最近实验晶格参数非常接近 [27]。在这个结构中，唯一的一个自由参数是 O (=x ）。原子位置的收敛是通过作用在每个原子上的小于 1.0 mRy/a.u. 的力来判断的。

结果与讨论

波段结构

图 2 显示了来自第一性原理的 Tl2Mo2O7、Sn2Nb2O7 和 Bi2Ti2O7 的能带色散。首先，我们关注中间面板 Sn2Nb2O7。获得的波段色散与先前的研究非常吻合，而没有提到准平坦波段的存在[19, 28]。我们看到价带顶部的形状 (- 3~0 eV) 类似于图 1b 中所示的紧束缚模型。这个一致性相当令人惊讶，因为这个模型只使用了两个参数，ε 和 t .因此，作为第一个近似值，Sn2Nb2O7 的价带由“Sn-s”轨道组成的 TB 带描述。在这里，我们注意到这些“Sn-s”轨道是由 Sn-s 和 O'-p 轨道组成的反键轨道。 ab-initio 带和 TB 带之间的主要区别在于能量 ~ 0 eV 处的带平坦度，这意味着除了最近邻的 Sn 原子之外，还需要跳跃积分来精确拟合 ab-initio 带.

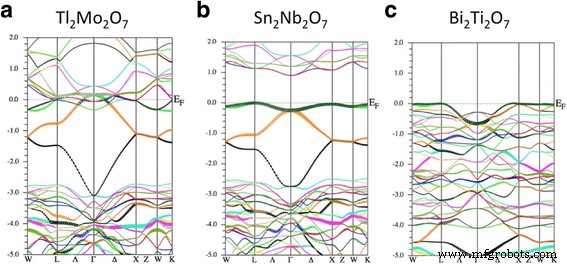
(a的电子能带结构 ) Tl2Mo2O7, (b ) Sn2Nb2O7, 和 (c ) Bi2Ti2O7。能量单位是eV。

接下来，我们讨论 Tl2Mo2O7 的能带结构，如图 2 左图所示。我们可以看到 Tl2Mo2O7 的价带形状与 Sn2Nb2O7 的价带形状几乎相同，表明 Tl2Mo2O7 中存在平带.然而，导带降低了它的能量并且带隙坍塌。与 Sn2Nb2O7 的情况不同，Mo-d 带被部分占据，表明形式离子构型 Tl ¹⁺ 2Mo ⁶⁺ 2O ²⁻ 7 不合适。这个结果表明点电荷模型的分析是非常有效的，这表明 A ¹⁺ 2B ⁶⁺ 2O7 不是烧绿石氧化物的稳定构型。 Tl-s 平坦带与 Mo-d 带纠缠，类似于类似烧绿石氧化物 Tl2Ru2O7 [29] 的情况。在 Tl2Ru2O7 中发现了金属-绝缘体转变，其原因归因于隐藏的 Tl-s 平坦带 [30]。可以预期，如果合成的话，这种金属-绝缘体转变也将发生在Tl2Mo2O7中。

最后，我们讨论了 Bi2Ti2O7 的能带结构，如图 2 的右侧面板所示。获得的能带色散与之前的研究 [31] 非常吻合。尽管 Bi2Ti2O7 和 Sn2Nb2O7 的价带形状不同，但 Bi2Ti2O7 的价带顶部在布里渊区的大部分对称轴上非常平坦。由于带的形状与图 1 不同，因此不能简单地在烧绿石晶格上的平坦带中找到该部分准平坦带的起源。然而，准平坦带和由此产生的高态密度 (DOS) 足以在掺杂空穴时实现铁磁性。我们将在下一小节讨论这一点。

铁磁态

在上一小节中，我们在 Sn2Nb2O7 的价带顶部发现了一个准平坦带。对于 Bi2Ti2O7，我们还发现了部分准平坦带。由于它们是绝缘体，我们必须在准平坦带中引入空穴以诱导铁磁性。在完美的扁平带的情况下，任何 现场库仑相互作用的价值 U 当平带半填充时，会导致铁磁基态 [4]。这意味着即使是扩展良好的原子 s 或 p 轨道也会导致铁磁基态。对于准平坦带的情况，数值研究表明，某个大的U> U c 可以诱发铁磁性，其中 U c 是临界值，U c 具有带宽 W 的顺序 [32]。由于 U 的估计 和 U c 在实际化合物中是困难的，我们进行了自旋极化 ab-initio 计算。考虑到能带计算已经成功地描述了同样具有窄能带的 bcc Fe 的铁磁基态，我们的方法将是合理的。为了模拟空穴掺杂，我们用 N 代替 O'，即我们计算了 Sn2Nb2O6N 和 Bi2Ti2O6N。由于这种取代减少了每个原始晶胞的两个电子（每个公式单位一个电子），因此准平坦带变为半填充。

图 3 显示了 Sn2Nb2O6N 和 Bi2Ti2O6N 的 DOS 曲线。上述准平坦带在费米能级附近形成一个尖峰。我们可以看到这两种化合物都变成了半金属，即能量为 E 的电子的自旋态 =E F（费米能量）是完全极化的。总磁矩M 两种化合物的每个原始晶胞均为 2.00 μB，这也表明传导电子是完全自旋极化的。上旋带和下旋带之间的交换分裂对于 Sn2Nb2O6N 为 ~ 0.3 eV，对于 Bi2Ti2O6N 为 ~ 0.4 eV。这些值远小于 bcc Fe 中的交换分裂，~ 2 eV。由于交换分裂大约由原子波函数决定 [33]，d 波段比 s 或 p 波段具有更大的交换分裂。然而，由于Sn2Nb2O6N和Bi2Ti2O6N的带宽很小，交换分裂超过了带宽，实现了半金属基态。

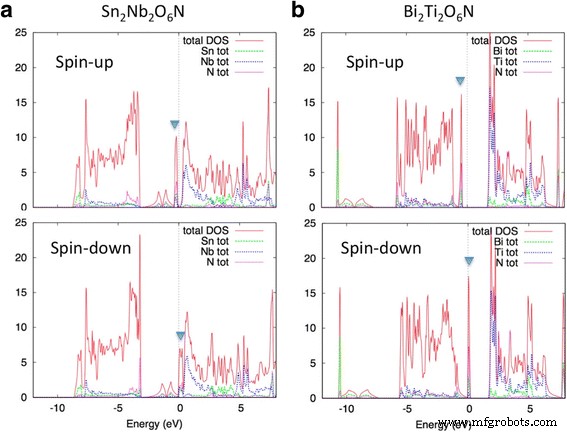
(a 的 DOS 曲线 ) Sn2Nb2O6N 和 (b ) Bi2Ti2O6N 为自旋极化状态。实心三角形表示准平带位置

结论

在本文中，我们展示了设计平带化合物的指导原则。根据这一原理，我们选择了三种烧绿石氧化物，并通过第一性原理研究了它们的电子结构。结合紧束缚分析，我们发现一些化合物实际上具有准平坦带。我们还发现，尽管这些化合物不含磁性元素，但对这些化合物的空穴掺杂会导致铁磁基态。这些发现将是实现化合物中平带系统和不含磁性元件的铁磁体的一大步。

缩写

DOS：

态密度

FLAPW：

全电位增强平面波

结核病：

紧束缚