在垂直磁化赛道中电流诱导的畴壁运动和倾斜

背景

赛道中的电流感应磁畴壁运动 (CIDWM) 揭示了一种新开发的磁性赛道存储设备 [1, 2]。由于这个充满希望的前景，在过去的几十年里已经进行了大量的工作。 CIDWM 首先在具有面内磁各向异性的铁磁体 (FM) 中进行研究，自旋极化电流产生的自旋转移矩 (STT) 作为驱动力 [3, 4]。之后，CIDWM 也在具有垂直磁各向异性 (PMA) [5, 6] 的 FM 中实现。然而，在一些 PMA 材料中，畴壁 (DW) 运动方向与电子流动方向相反，这与 STT [7, 8] 的预测相矛盾。并且发现更多的工作是在带有 PMA 的重金属 (HM)/FM 双层结构中 DW 运动是沿着电流方向的。结果表明，由于 FM 的结构反转不对称性，通过自旋霍尔效应和/或 Rashba 效应产生的 HM 产生的自旋轨道扭矩 (SOT) 以及界面 Dzyaloshinskii-Moriya 相互作用 (DMI) 被认为驱动手性 DW 运动沿当前方向 [9, 10]。因此，为了提高 CIDWM 的效率，需要具有大自旋霍尔角 (θ SH ) 产生更大的扭矩来驱动 DW 运动。许多努力已经致力于获得一个大的θ SH 通过改变 HM 的厚度 [11, 12]，装饰 HM 和 FM 之间的界面 [13, 14]，改变 HM 的结晶度 [15]，甚至在 HM 中加入氧 [16]，来改变 HMs。此外，一些报告也取得了较大的有效θ SH 基于HM/FM/HM结构，其中两个HM层具有相反的θ符号 SH [17,18,19]。当电流通过两个 HM 层时，两种 HM 层产生的自旋电流将协同工作以提高 SOT 效率，从而降低电流密度以切换磁化或驱动 DW 运动。同时，这种三层的 DMI 强度可能与双层不同，因为在 FM 层的两侧有两个界面相互作用。当提出扩展的集体坐标模型来解释 DW 倾斜行为时，发现 DMI 强度对 DW 速度有很大影响 [20]。此外，在 GaMnAs 微线中也报道了 DW 倾斜 [20,21,22]。

在我们之前的工作中，我们研究了在 Co 和 Ta 之间插入 C 夹层对 PMA 的 Pt/Co/Ta 结构中的各向异性场、开关场和 SOT 有效场的影响 [23]。得到的磁化开关电流密度为10 ⁶ A/cm ² 在 Pt/Co/Ta 和 Pt/Co/C/Ta 器件中。在这项工作中，我们研究了这两个样品中电流引起的 DW 运动和倾斜行为，以及 C 插入对微型 Pt/Co/Ta 赛道中 DMI 强度和 DW 速度的影响。我们发现计算的 DMI 交换常数 (|D |)，表明 DMI 强度主要来自 Pt/Co/Ta 和 Pt/Co/C/Ta 堆叠中 Pt/Co 界面的贡献。在场致 DW 运动中，即使在大磁场下，测得的 Pt/Co/C/Ta 中的 DW 速度也小于 Pt/Co/Ta 中的速度，表明钉扎势垒对 DW 运动有很大影响。此外，在 CIDWM 中，与在当前产生的有效场和施加的磁场之间具有相同幅度的场感应运动中观察到的 DW 速度更大。它表明电流产生的焦耳热也会影响 DW 运动。更重要的是，在Pt/Co/Ta和Pt/Co/C/Ta堆叠中观察到了电流引起的DW倾斜现象，这可以用电流产生的奥斯特场结合自旋霍尔有效场很好地解释。

方法

两个薄膜叠层 Ta(3)/Pt(5)/Co(0.6)/Ta(5) 和 Ta(3)/Pt(5)/Co(0.6)/C(2)/Ta(5)（厚度在nm) 在室温下通过直流磁控溅射沉积在康宁玻璃基板上，基础压力低于 4.0 × 10 ^-5 Pa。底部 3 nm Ta 用作种子层，顶部 Ta 层由于暴露在空气中而具有大约 1.5 nm TaOx 覆盖层 [17, 24]。然后，使用标准光刻和 Ar 离子铣削技术将薄膜堆叠图案化为 8.5-μm 和 3.0-μm 宽的 Pt/Co/Ta 和 Pt/Co/C/Ta 跑道，以研究 CIDWM。此外，使用相同技术图案化的 8.5 微米宽霍尔条用于测量面外场 (H z ) 依赖的异常霍尔电阻 (R 大厅 ) 在不同的面内偏置场 (H x ) 沿电流方向实现自旋霍尔有效场 (H 她 ) 并估计 Pai 等人报告的 DMI 强度。 [25]。在他们的报告中，R 的转变 大厅 -H z 在 H 处循环 x 可以用手性 Néel DW 模型很好地解释。偏移定义为 H 她 , 可用于量化 SOT 效率 χ ≡ H 她 /J (J 是充电电流密度）。在这项工作中，该方法用于表征 DMI 强度和 SOT 效率。此外，利用具有极性克尔效应的磁光克尔显微镜在室温下监测外加场或电流脉冲下的DW运动。

结果与讨论

基于手征 Néel DW 模型，我们首先研究了面内偏置场 H 下的异常霍尔环 x 获得 DMI 强度和 SOT 效率（参见附加文件 1）。得到的DMI有效场(H DMI ) 对于 Pt/Co/Ta 和 Pt/Co/C/Ta，分别约为 1370 和 1055 Oe。饱和 χ (χ ^坐 ) 代表最大 SOT 效率约为 10.0 和 8.3 Oe/(10 ⁶ A/cm ² ) 分别为 Pt/Co/Ta 和 Pt/Co/C/Ta。下降的χ ^坐 对于 Pt/Co/C/Ta 可能是因为 Co 和 C 之间的界面以及 C 和 Ta 之间的界面的一些相互扩散和化学反应增加了自旋翻转概率并减少了从顶部 Ta 的自旋电流的有效注入.此外，DMI 交换常数的强度|D |也可以从测得的|H DMI |使用 |D | =μ 0M s Δ |H DMI | [26]，其中Δ 是 DW 宽度，它与交换刚度常数 A 有关 和有效 PMA 能量密度 K 效果 通过∆ =(A /K 效果 ) ^1/2 .使用 M s （分别约为 1.213×10 ⁶ 和 1.288×10 ⁶ A/m 用于 Pt/Co/Ta 和 Pt/Co/C/Ta) 和 K 效果 （分别约为 4.1×10 ⁵ 和 2.1×10 ⁵ 焦/米 ³ 为 Pt/Co/Ta 和 Pt/Co/C/Ta)，如先前工作中所报告并假设 A ≈ 1. 5 × 10 ⁻¹¹ J/ m [27]，我们估计 |D | =1.01 ± 0.16 mJ/ m ² 对于 Pt/Co/Ta 和 |D | =1.15 ± 0.14 mJ/ m ² 对于 Pt/Co/C/Ta。 |D 的区别 |这两个样本的价值似乎很弱。这可能是由于总 DMI 强度来自底部 Pt/Co 界面和顶部 Co/Ta 或 Co/C 界面的两个贡献。由于底部 Pt/Co 界面非常相似，它们对 |D 的贡献相同 |。而对于来自顶部 Co/Ta 或 Co/C 界面的贡献，Ma 等人。 [28] 报道 |D | Ta 的诱导比 Pt 弱得多。因此，顶部 Co/Ta 界面对于总 |D 的贡献较弱 |。由于 C 的自旋轨道耦合非常弱，顶部 Co/C 界面的贡献也可以忽略不计。 还注意到底部 Pt/Co 和顶部 Co/Ta 界面都对 DMI 有贡献，但可能会部分抵消彼此 [28]，导致 |D | Pt/Co/Ta 样品与 Pt/Co/C/Ta 样品的比较。因此，类似的 |D | Pt/Co/Ta 和 Pt/Co/C/Ta 样品表明 DMI 强度主要来自 Pt/Co 界面的贡献。此外，对于这两个样本，H DMI /H K （对于 Pt/Co/Ta 和 Pt/Co/C/Ta 分别约为 0.2 和 0.3）小于 2/π。虽然 H DMI 没有超出稳定 Néel DW 所需的理论阈值 [25, 26]，这两个样品中的手性 Néel DW 通过观察 CIDWM 行为来证明，这将在下面讨论。同时，在面内偏置场 (H 是 ) 正交电流方向也进行了研究。即使一个很大的H 是 应用，R 的移位 大厅 -H z 循环非常小（请参阅附加文件 1）。可能是因为 H 是 逐渐将手性 Néel 型 DW 转变为 Bloch 型 DW，有效场 H 她 根据公式 [10, 29, 30]，对于布洛赫型 DW 几乎为零：

其中，θ 她 , 女士 , t F , J x , \( \widehat{m} \) 和 \( \widehat{j} \) 表示有效自旋霍尔角、FM 层的饱和磁化强度、FM 层的厚度、沿 x 的电流密度 方向、磁化强度单位矢量和电流密度单位矢量。

接下来，DW 速度 (v ) 在面外磁场和面内电流脉冲下使用克尔显微镜测量以研究 DW 运动行为。在跑道在相反的大磁场下饱和后，使用刚好在成核场上方的磁场脉冲形成预先准备的 DW。 H下的速度 z 两个样品的脉冲如图 1a、b 所示。对于 Pt/Co/C/Ta，v 即使在大驱动磁场下，仍小于 Pt/Co/Ta 样品。这可能是由于 C 装饰后形成的缺陷更多，这增加了钉扎场 [23]。也可以看出 lgv 与 H 成正比 z ^-1/4 ，根据蠕变定律 [31] 表明 DW 运动的蠕变状态：

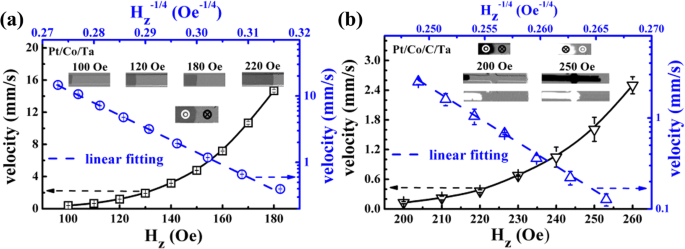
作为面外场函数的 DW 速度 H z 对于 Pt/Co/Ta (a ) 和 Pt/Co/C/Ta (b ）。 a 中的插图 和 b 代表不同领域域的快照以显示DW形状

其中 U C 是与无序引起的钉扎电位相关的特征能量，k B 是玻尔兹曼常数，T 是温度，H 部门 是塞曼能量等于 DW 钉扎能量的去钉扎场。拟合斜率给出了 \( \frac{U_c}{k_BT}{H_{dep}}^{1/4}=s \), s 大约是 37.4 和 76.5 Oe ^1/4 分别为 Pt/Co/Ta 和 Pt/Co/C/Ta。由于 H 部门 Pt/Co/C/Ta 比 Pt/Co/Ta 大两倍 [23]，H 部门 ^1/4 它们之间小于 1.5。但是，s 的区别 它们之间的比值大于 2，说明 Pt/Co/C/Ta 样品具有较大的钉扎电位，这与上述讨论一致。此外，图 1a、b 中的插图还显示了不同磁场下域图像的快照。可以看到，Pt/Co/C/Ta 的 DW 形状比 Pt/Co/Ta 的分布更大。它还表明，由于 C 装饰引起随机分布的钉扎位点，Pt/Co/C/Ta 中的钉扎电位不是很均匀。而这两个样品在磁场下没有观察到规律的DW倾斜，这与理论集体坐标模型[20]不同。

之后，还研究了 CIDWM 行为以与场引起的 DW 运动进行比较。由饱和状态的脉冲磁场首先使自上而下 (UD) 或自下而上 (DU) 域成核，然后使用脉冲发生器施加脉冲电流以推动 DW 运动5-100 ns 范围内的脉冲宽度。图 2a、b 显示了未施加任何磁场的 CIDWM 速度。正或负速度表示 DW 沿或逆当前方向运动。这意味着在这两个样品中存在 DMI 时，手性 Néel DW 的形成 [10, 30]。较高电流密度下的速度增加是由于 H 她 作用于手性 Néel DW。然而，与 Pt/Co/Ta 结构相比，它需要两倍大的电流密度才能在 Pt/Co/C/Ta 中达到相同的 DW 速度。这可能是由于 C 界面装饰降低了 SOT 效率和增加了钉扎势垒。此外，电流驱动的 DW 速度约为 10 ³ 电流产生的有效场保持与磁场相同的值，比通过磁场驱动大数倍。它揭示了其他机制，如焦耳加热和/或电流产生的奥斯特场，也可能在 CIDWM 中发挥重要作用。应该注意的是，在图 2b 和图 3c 中，当电流密度为 ± 19.2 MA/cm² .同时，人们可以在图 1 和图 2 的插图中看到更多的成核区域，如白点或黑点。 2b 和 3c 在更高的电流密度下。这可能是由于存在大的焦耳热，热激活了大电流密度下的一些随机成核位点，并且钉扎势垒景观也可以重新分布，这会对运动速度和倾斜角产生影响。 <图片>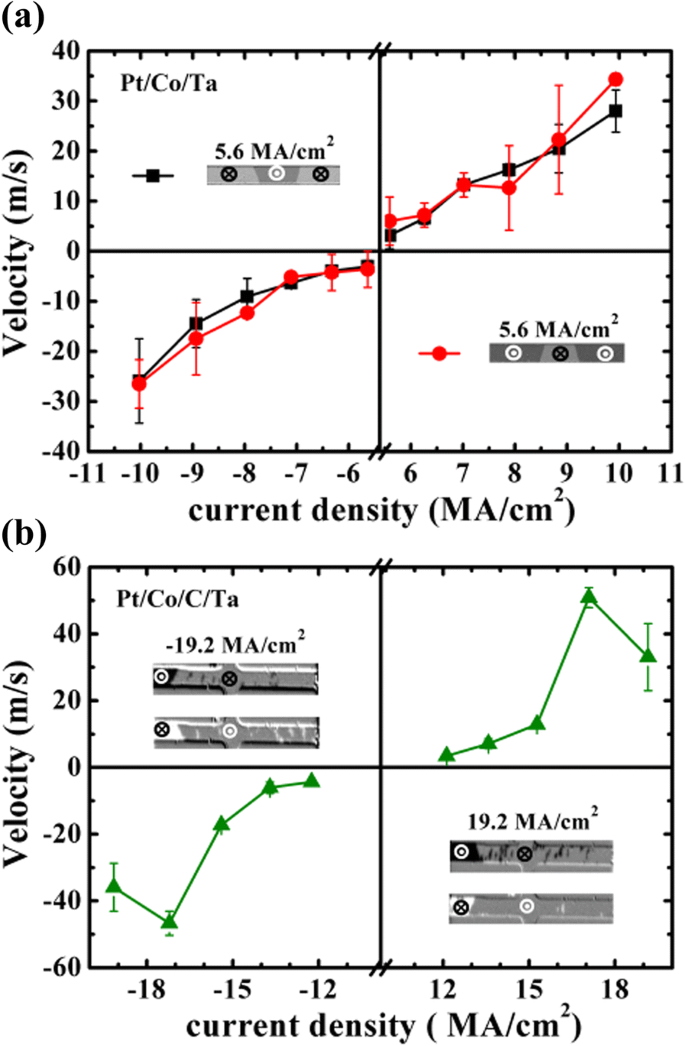

DW 速度对 Pt/Co/Ta (a ) 和 Pt/Co/C/Ta (b ）。 a 中的插图 和 b 代表在代表电流密度下域形状的快照

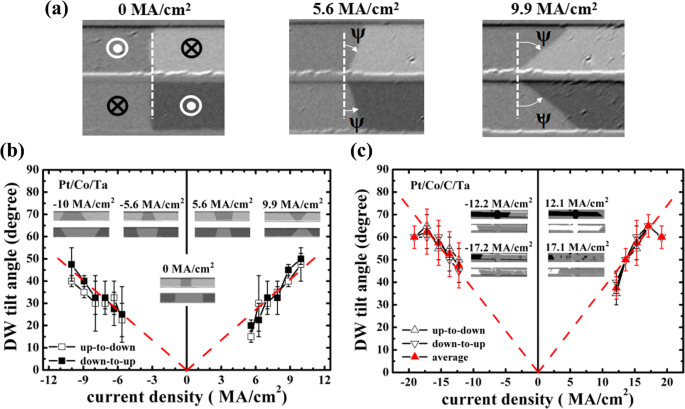
(a ) Kerr 图像给出了 DW 倾斜角的定义 (ψ ) 和 ψ 的变化 以 Pt/Co/Ta 样品为例，在从“上”到“下”状态和“下”到“上”状态的不同电流密度下。 DW 倾斜角与 Pt/Co/Ta 的电流密度 (b ) 和 Pt/Co/C/Ta (c ）。 b 中的插图 和 c 表示不同电流密度下域形状的快照

在电流引起的 DW 运动过程中，在这两个样品中可以清楚地观察到 DW 倾斜现象，并且倾斜是在具有足够短脉冲作为驱动力的时间相关观察中逐渐形成的。为了深入了解电流引起的 DW 倾斜，我们测量了 DW 倾斜角 (ψ )，它在图 3a 中定义为不同的电流密度。还应注意的是，由于沿跑道的脱销分布较宽，在运动过程中倾斜角可能会略有变化，这将导致特定电流密度下的较大测量误差。从图 3b，c 可以看出倾斜角对两个样品的电流密度的大致线性依赖性。它与之前的理论工作 [20] 一致，其中可以观察到倾斜角和 DW 速度对较低电流密度的近似线性依赖性。然而，在他们的模拟中，大的 DW 倾斜角发生在电流密度至少大一个数量级的情况下。这与我们的观察结果不一致，并且在我们的实验中场致 DW 运动期间也未观察到倾斜行为。因此，DMI 或钉扎势垒的分级分布对电流引起的 DW 倾斜的影响可能很弱。此外，异常霍尔效应也可能导致 DW 倾斜，但预计在纳米厚的赛道中贡献很小 [20]。一种可能的解释是施加的电流不仅产生自旋霍尔有效场 H 她 , 还有奥斯特场 (H 奥斯特 ) 这也可能导致 DW 运动。两者 H 她 和 H 奥斯特 可能会影响 DW 倾斜。在图 4 中，我们绘制了这些有效场的草图，以阐明 DW 倾斜行为。域排列显示为 U-D-U-D 草图，具有左手手性的 DW 中的磁化显示为沿面内方向的细黑色箭头。在薄而均匀的跑道上，如果厚度 (t ) 远小于宽度 (w )，生成的 H 奥斯特 集中在两个边缘，其在厚度上的平均分量可以通过 H 计算 奥斯特 = ±jt [3 + 2lnw /t ]/4π [22]。得到的H 奥斯特 使用 10.0 和 19.2 MA/cm ² 的最大电流密度时，Pt/Co/Ta 和 Pt/Co/C/Ta 的电流密度约为 19.6 和 37.4 Oe , 分别相当于自旋霍尔有效场 H 她 （在相同的电流密度下，Pt/Co/Ta 和 Pt/Co/C/Ta 约为 100.0 和 159.4 Oe）。由于 H 她 和 H 奥斯特 在标有绿色星星的位置具有相同的方向，更大的有效场将作用在绿色星星区域的 DW 上，这导致与赛道中绿色星星的相对区域相比更大的速度。因此，可以形成具有特定梯形形状的倾斜 DW，如图 4 的左下图所示。图 3b 中 Pt/Co/Ta 的插图也明显显示了某些代表性电流密度下的类似形状。此外，在较高电流密度下倾斜角的增加可能是由于 H 的增加导致跑道两侧的速度差异较大 奥斯特 .同时，根据上述分析可以发现，一旦畴的排列和/或电流极性发生变化，畴的形状就会发生变化。电流脉冲处的所有勾画域形状与实验观察一致。此外，当面内 H x 或 H 是 被申请;被应用。当 H x 应用，它将改变 DW 中的磁化方向。因此，H 她 将改变 DW 的符号，其原始水平磁化与 H 相反 x ，这使得梯形域扩大或缩小（取决于 H 的符号 x ) 如图 4 的右中间面板所示。当 H 是 应用，强H 是 会将 Néel 型 DW 更改为 Bloch 型。 H 她 根据等式将变为零。 (1)，并且只有当前生成的 Oersted 场 H 奥斯特 驱动 DW 运动。这将使域在一侧扩展。还可以看到边缘域的变化发生在 H 是 约为 − 1400 Oe，如图 4 的右下图所示。这与 H 的分析一致 奥斯特 作为唯一的驱动力负责 DW 运动。但是，它不能导致常规的 DW 倾斜行为。因此，电流引起的DW倾斜可以归因于电流引起的奥斯特场与自旋霍尔有效场的结合。

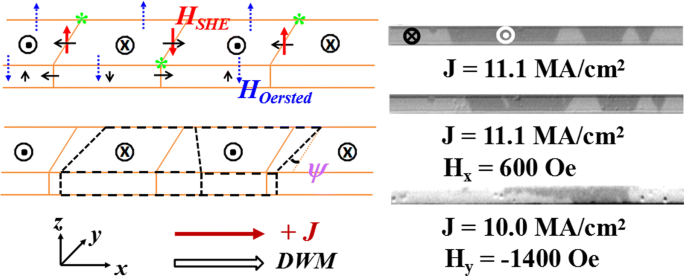
在电流密度 J 下的 DW 运动示意图和域形状 .左上图显示了带有 U-D-U-D 草图的域以及域和 DW 中的磁化方向（黑色细箭头）。一旦施加电流，生成的 H 她 作用在 DW 上的用红色粗箭头表示，而奥斯特场 (H 奥斯特 ) 在赛道的两侧显示为蓝色虚线箭头。左下图显示了在H作用下域形状的相应变化（用虚线粗黑块表示） 她 和 H 奥斯特 .右图显示了面内磁场对 Pt/Co/Ta 磁畴形状的影响

结论

总之，在 Pt/Co/Ta 和 Pt/Co/C/Ta 结构中观察到电流引起的畴壁运动和倾斜。 DMI强度和SOT效率是使用传输测量方法获得的，可以达到1.01 ± 0.16（1.15 ± 0.14）mJ/m ² 和 10.0 (8.3) Oe/MA/cm ² 分别用于 Pt/Co/Ta (Pt/Co/C/Ta) 样品。 Pt/Co/Ta 和 Pt/Co/C/Ta 样品的相似 DMI 强度表明 DMI 强度主要来自 Pt/Co 界面的贡献。 Pt/Co/C/Ta 的场致 DW 运动中降低的 DW 速度表明 DW 速度与钉扎势垒有关。此外，电流产生的焦耳热和奥斯特场在 DW 运动和倾斜中起着重要作用。对于赛道内存应用，应考虑大电流产生的奥斯特场，因为它会显着改变记录位的形状，甚至缩小记录位的面积。这可能不利于实际应用。我们的发现可以为在基于 SOT 的赛道记忆中驱动 DW 运动提供一些设计前景。

缩写

CIDWM：

电流诱导畴壁运动

DMI：

Dzyaloshinskii-Moriya 互动

D-U：

自下而上

DW：

领域墙

FIDWM：

场致畴壁运动

FM：

铁磁体

HM：

重金属

PMA：

垂直磁各向异性

SOT：

自旋轨道扭矩

STT：

自旋转移扭矩

U-D：

从上到下