基于碳纳米管的纳米线谐振器机电振荡中几何相位的特性
摘要
几何相位是振动波函数中的额外相位演化,可能适用于广泛的科学和技术。采用不变算子方法研究了基于碳纳米管的纳米线谐振器在挤压状态下的几何相位特性。线性不变算子的引入对于处理复杂的瞬态哈密顿系统很有用,使我们能够推导出几何相位的解析公式。利用这一点,我们根据相关说明分析了几何相位的时间行为。研究了挤压参数对几何相演变的影响。几何相位大体上振荡,并且这种振荡的包络随时间增加。当振荡的经典振幅、阻尼因子和驱动力的振幅等参数较大时,几何相位的增加率较大。我们已经确认,在系统的角频率接近谐振角频率的情况下,几何相位会随时间急剧增加。我们对几何相位特征的研究对于理解纳米线振荡的拓扑特征至关重要。
介绍
最小谐振器的机械振动,例如碳纳米管(CNT-based)纳米线 [1-3]、半导体纳米线 [4]、石墨烯 [5] 和悬浮粒子 [6],一直是主要研究课题在纳米科学界工作了十多年。关于由外部周期性力驱动的纳米线谐振器的机电振荡的积极研究已经在理论和实验领域进行。特别是,基于 CNT 的纳米线谐振器作为纳米级机械装置引起了相当大的兴趣,因为它们对来自周围环境的小扰动具有高质量因素的非凡敏感性。基于悬吊式 CNT 的纳米线谐振器是测量各种物理量(例如 EM 波 [2]、小力 [7]、质量 [8]、温度 [9] 和噪声 [10])的设备的有希望的候选者。
为了从理论上阐明系统的基本特征,需要对纳米线振荡中的量子相位演化进行分析。关于基于 CNT 的纳米线谐振器的量子振动态 [11],几何相位 [12] 以及通常的动态相位作为该相位的补充演化出现。几何相位 [12] 是一个量子态的不对称性,可以应用于不同的物理领域。几何相位分析可用于表征纳米线的纳米特性,例如共振曲线 [13, 14]、强量子振动 [15, 16]、应变弛豫机制 [17, 18]、狄拉克磁等离子体的出现[19], 以及 Aharonov-Bohm 振荡的拓扑结构 [20].
对与非绝热动力学相关的几何相位的研究可以为纳米力学系统提供见解,这对于精确模拟技术的进步是必要的 [21]。量子态的制备、操纵和检测是量子技术中的重要因素。本研究的目的是阐明在纳米线振荡的量子态中发生的几何相位的时间行为。为了理解基于 CNT 的纳米线振动的机制,我们将研究压缩状态下几何相位的时间演化,压缩状态是一种类似经典的量子状态,如相干状态。压缩状态的优点是在该状态下正交的不确定性可以显着降低,代价是增加另一个正交的不确定性,而在相干状态下这种不确定性调制是不可能的。我们将特别分析共振对几何相位的影响。由于共振能量与非共振状态的能量显着不同 [22, 23],波函数的拓扑行为很重要,可能与正常情况下的拓扑行为有很大差异。也将严格分析物理参数和挤压参数的变化对几何相演变的影响。几何相位在动力系统中无处不在 [24],可以应用于各种现代技术,例如量子计算 [25]、强度干涉测量 [26]、光子多任务 [27]、量子传感协议 [28] 和波-稳定性测量[29]。
系统的哈密顿量涉及与系统阻尼和外部驱动力相关的时间函数。因此,该系统是一种时间相关的哈密顿系统(TDHS),其量子力学问题直到最近才被广泛研究。 TDHS的哈密顿量中的时间函数在大多数情况下不能与典型变量的函数分离,导致求解薛定谔方程的常规分离变量方法不可用。为克服这一困难而开发的另一种强大方法是由 Lewis 和 Riesenfeld [30, 31] 引入的不变算子方法。当我们推导出 TDHS 的量子解时,这种方法是一个非常有用的数学工具。许多由 TDHS 描述的量子力学问题都是基于这种方法进行研究的。例如,它们包括混沌粒子散射 [32]、光在时变介质中的传播 [33]、捕获驱动电子的控制 [34] 和量子纳米电子电路的非经典性 [35]。 TDHSs的量子力学处理方法还有多种,包括酉变换法[36]、李代数法[37]和哈密顿估计法[38]。
对于系统是TDHS,我们使用不变算子的方法来获得系统的量子解。将介绍用湮灭算子表示的线性不变算子。由于系统的时间依赖性,湮灭和创造算子以时间表示,使用这些梯形算子可以获得相干和压缩状态。系统的几何相位将通过利用压缩状态下的波函数进行分析评估。几何相位的时间演化将在其插图的基础上进行详细分析,并具有多种参数选择。
方法
为了研究几何相位,我们首先需要建立纳米线尖端的经典运动方程。因为几何相位出现在 TDHS 的量子波演化中,所以有必要推导出我们管理的特定量子态的波函数。我们将考虑介绍部分中提到的挤压状态。 TDHS 不同量子态的波函数,包括压缩态,可以通过不变算子方法获得。
随时间变化的幅度x的运动方程 对于有效质量m的悬浮碳纳米管的弯曲模式 由 [1]
给出 $$ \ddot{x}+\left(\frac{\omega_{0}}{Q} +\eta x^{2}\right) \dot{x}+\left(\omega_{0}^{ 2}+\beta x^{2}\right) x =f_{\mathrm{d}}\cos (\omega t), $$ (1)其中 ω 0 是谐振角频率,Q 品质因数,f d 静电驱动力除以 m , η 非线性阻尼系数,β 达芬参数。为方便起见,让我们假设尖端的位移相对于 CNT 线长度足够小。然后,我们可以忽略方程中的非线性项。 (1)、导致[2]
$$ \ddot{x}+\frac{\omega_{0}}{Q} \dot{x}+\omega_{0}^{2} x =f_{\mathrm{d}}\cos (\omega t)。 $$ (2)产生方程的系统的哈密顿量。 (2) 由
给出 $$ \hat{H}=e^{-\gamma t} \frac{\hat{p}^{2}}{2m} +\frac{1}{2}me^{\gamma t} \left [\omega_{0}^{2} \hat{x}^{2} - 2f_{\mathrm{d}}\cos (\omega t)\hat{x}\right], $$ (3)其中 γ =ω 0/Q .方程的经典解。 (2) 由互补函数X组成 c (t ) 和一个特定的解决方案 X p (t ),由
给出 $$\begin{array}{@{}rcl@{}} &&X_{c}(t)=X_{c,0}e^{-\gamma t/2}\cos(\Omega t+\varphi) , \end{array} $$ (4) $$\begin{array}{@{}rcl@{}} &&X_{p}(t) =X_{p,0}\cos (\omega t - \ delta), \end{array} $$ (5)其中 X c ,0 是一个常数,\(\Omega =\sqrt {\omega _{0}^{2} - \gamma ^{2}/4}\), φ 是任意相位,并且
$$\begin{array}{@{}rcl@{}} X_{p,0}&=&\frac{f_{\mathrm{d}}}{\sqrt{\left(\omega_{0}^ {2} -\omega^{2}\right)^{2} + \gamma^{2} \omega^{2}}}, \end{array} $$ (6) $$\begin{array} {@{}rcl@{}} \delta &=&\tan^{-1} \frac{\gamma \omega}{ \omega_{0}^{2} -\omega^{2}}。 \end{array} $$ (7)动量空间中的经典解以类似的方式给出,其中互补函数为 \(P_{c} (t) =me^{\gamma t} \dot {X}_{c}(t)\)并且特定的解决方案是 \(P_{p} (t) =me^{\gamma t} \dot {X}_{p}(t)\)。为了研究系统的几何相位,我们首先需要推导出量子解。注意方程中给出的系统的哈密顿量。 (3) 明确依赖于时间。为了推导出系统的量子解,我们使用不变算子方法[30, 31],这在我们处理这样一个时变系统时是一种有用的方法。系统的一个不变算子 \(\hat {I}\) 可以从刘维尔-冯诺依曼方程导出,它由 \({d \hat {I}}/{dt} ={\partial \hat {I}}/{\partial t} + \left [\hat {I},\hat {H}\right ]/\left (i\hbar \right) =0\)。因此,从插入方程后的严格评估。 (3) 在这个方程中,我们有一个形式为
的线性不变算子[34] $$ \hat{I} =\hat{A} e^{i\Omega t}, $$ (8)其中 \(\hat {A}\) 是由
给出的湮灭算子 $$ \begin{aligned} \hat{A} =&\left(2\hbar m\Omega\right)^{-1/2} \left[ m \left(\Omega+ i\frac{\gamma}{ 2} \right) e^{\gamma t/2}\left[\hat{x}-X_{p}(t)\right]\right.\\ &\left.+ie^{-\gamma t /2} \left[\hat{p}-P_{p}(t)\right]\! {\vphantom{\left(\Omega+ i\frac{\gamma}{2} \right)}}\right]。 \end{对齐} $$ (9)方程的厄米伴随。 (9), \(\hat {A}^{\dagger }\), 是创世算子。
我们可以将\(\hat {A}\)的特征值方程表示为
$$ \hat{A} |A \rangle =A |A \rangle. $$ (10)通过评估上述等式,我们得到特征值的表达式,使得
$$ A(t) =A(0) e^{-i\Omega t}, $$ (11)其中 A (0)=A 0e -i φ 与
$$ A_{0} =\left[m\Omega/(2\hbar)\right]^{1/2}X_{c,0}。 $$ (12)而相干态|A 〉是\(\hat {A}\)的本征态,压缩态是算子\(\hat {B}\)的本征态,由
给出 $$ \hat{B} =\mu \hat{A} + \nu \hat{A}^{\dagger}, $$ (13)其中 μ 和 ν 是产生方程的复变量
$$ |\mu|^{2} - |\nu|^{2} =1。 $$ (14)如果我们把\(\hat {B}\)的特征值方程写成
$$ \hat{B} |B \rangle =B |B \rangle, $$ (15)|B 〉是挤压状态。通过在配置空间中求解这个方程,我们有
$$ {\begin{aligned} \langle {x}|B\rangle =&^{4}\!\!\!\sqrt{\frac{m \Omega e^{\gamma t}}{\hbar\ pi(\mu-\nu)(\mu^{*}-\nu^{*})}} \exp \left\{- \frac{1}{\hbar (\mu-\nu)} \left [\frac{1}{2} me^{\gamma t}\left({\vphantom{\frac{1}{2}}}(\mu+\nu)\Omega \right.\right.\right. \\ &\left. +\frac{i\gamma}{2}(\mu-\nu)\right)\left[x-X_{p}(t)\right]^{2} -[iP_{ p}(t)(\mu-\nu)+ \left(2\hbar m \Omega e^{\gamma t}\right)^{1/2} \\ &\left. \left.\times(\mu A+\nu A^{*}) ]\left[x-X_{p}(t)\right] {\vphantom{\frac{1}{2} me^{\gamma t}}}\right]-\frac{|A|^{2}+A^{2}}{2(\mu-\nu)(\mu^{*}-\nu^{*})} \对\}。 \end{对齐}} $$ (16)因此,在挤压状态下的波函数已经被推导出为方程。 (16).基于对波函数的这种解析描述,可以阐明系统的量子特征。对于 μ =1 和 ν =0,方程(16) 化简为相干态的波函数,即方程的本征态。 (10) 在配置空间中。波函数,方程。 (16),将在下一节中用于推导挤压状态下的几何相位。
结果与讨论
众所周知,量子波演化中的相位包括几何相位和动力学相位。几何相位最早由 Berry 在 1984 年发现 [12],用于一个具有绝热变化的循环演化系统。根据量子力学中的绝热定理,在参数空间中循环演化的量子态的瞬时本征态稍后将保持在同一状态,同时量子相有额外的积累,即贝里相。 Berry 相以包括量子系统的非绝热、非循环和/或非幺正演化的方式的推广是几何相。
挤压状态下的几何相位由
给出 $$ \gamma_{G}(t) =\int_{0}^{t} \langle B(t') |i\frac{\partial}{\partial t'}| B(t') \rangle dt' +\gamma_{G}(0)。 $$ (17)波函数在构型空间中对时间的微分变为
$$ \frac{\partial \langle {x}|B\rangle}{\partial t} \,=\, \left\{ f_{1}(t) \!\left[x-X_{p}( t)\right]^{2}\,+\,f_{2}(t) \left[x\,-\,X_{p}(t)\right]\,+\,f_{3}( t) \right\}\! \!\langle {x}|B\rangle, $$ (18)哪里
$$ f_{1}(t) =- \frac{m\gamma e^{\gamma t}}{2\hbar (\mu-\nu)} \left((\mu+\nu)\Omega + \ frac{i\gamma}{2}(\mu-\nu) \right), $$ (19) $$ {\begin{aligned} f_{2}(t) &=\frac{1}{\hbar (\mu-\nu)}\left[ \left((\mu+\nu)\Omega + \frac{i\gamma}{2}(\mu-\nu) \right) P_{p}(t) -ime^{\gamma t} \right.\\ &\quad\times\left[\omega_{0}^{2} X_{p}(t) - f_{\mathrm{d}} \cos(\ omega t)\right](\mu-\nu) +\left(2\hbar m \Omega e^{\gamma t}\right)^{1/2} \\ &\quad \left.\times\ left(\frac{\gamma}{2}\left(\mu A + \nu A^{*}\right)-i\Omega \left(\mu A - \nu A^{*}\right) \ right) \right], \\ \end{aligned}} $$ (20) $$ {\begin{aligned} f_{3}(t) &\!=\frac{\gamma}{4}-\frac {1}{\hbar me^{\gamma t}(\mu-\nu)} \left[iP_{p}(t)(\mu-\nu) + \left(2\hbar m\Omega e^ {\gamma t}\right)^{1/2} \right.\\ &\quad\left.\times\left(\mu A+\nu A^{*}\right){\vphantom{\left( 2\hbar m\Omega e^{\gamma t}\right)^{1/2}}}\right] P_{p}(t)+ \frac{i\Omega A^{2}}{(\ mu-\nu)\left(\mu^{*}-\nu^{*}\right)}。 \end{对齐}} $$ (21)插入方程后的进一步评估。 (18) 进入方程。 (17) 给
$$ {\begin{aligned} \gamma_{G}(t) =&\int_{0}^{t} dt' \left[ A_{0}^{2}\left(\frac{\gamma^{ 2}}{4\Omega}+\Omega + g_{1} \sin\left[2\left(\Omega t'+\varphi\right)\right] +g_{2} \cos\left[2\ left(\Omega t'+\varphi\right)\right] \right) \right.\\ &\left.-A_{0}\left[ g_{3}(t') \sin\left(\Omega t'+\varphi\right) +g_{4}(t') \cos\left(\Omega t'+\varphi\right) \right]+ g_{5}(t') {\vphantom{\frac {\gamma^{2}}{4\Omega}}}\right] +\gamma_{G}(0), \end{aligned}} $$ (22)哪里
$$\begin{array}{*{20}l} g_{1}~ &=\frac{\gamma}{2} + \frac{i\Omega \left(\mu\nu^{*}-\ mu^{*}\nu\right)}{(\mu-\nu)\left(\mu^{*}-\nu^{*}\right)}, \end{array} $$ (23) $$\begin{array}{*{20}l} g_{2}~ &=\frac{\gamma^{2}}{4\Omega}+\Omega\frac{2|\nu|^{2 }- \left(\mu\nu^{*}+\mu^{*}\nu\right)}{(\mu-\nu) \left(\mu^{*}-\nu^{*} \right)}, \end{array} $$ (24) $$\begin{array}{*{20}l} g_{3}(t) &=\left(\frac{2\Omega}{m \hbar e^{\gamma t}} \right)^{1/2}P_{p}(t), \end{array} $$ (25) $$ {\begin{aligned} g_{4}( t) =\frac{1}{\sqrt{2\hbar\Omega}}\left(\frac{\gamma }{\sqrt{me^{\gamma t}}}P_{p}(t) - 2 \sqrt{me^{\gamma t}}\left[\omega_{0}^{2} X_{p}(t) - f_{\mathrm{d}} \cos(\omega t)\right]\右), \end{aligned}} $$ (26) $$ {\begin{aligned} g_{5}(t) &=\frac{P_{p}^{2}(t)}{\hbar me ^{\gamma t}}+\frac{\gamma^{2}}{8\Omega}\left[2|\nu|^{2}-\left(\mu\nu+\mu^{*}\ nu^{*}\right) +1\right] \\ &\quad +\frac{i\gamma}{4(\mu-\nu)\left(\mu^{*}-\nu^{* }\right)} \left[|\mu|^{2}\left(\nu^{2}-\nu^{*2}\right)-|\nu|^{2}\lef t(\mu^{2}-\mu^{*2}\right)\right.\\ &\quad\left.+ (2|\nu|^{2}+1)\left(\mu\ nu^{*}-\mu^{*}\nu\right) +(\mu-\mu^{*})(\nu-\nu^{*})\right]。 \end{对齐}} $$ (27)g 中的最后一项 5 包含 (μ -μ * )(ν −ν * ) 作为一个相位是不够的,因为这是一个纯虚数。因此,我们现在通过选择至少一个 μ 和 ν 作为一个真正的价值。这种补救措施总是可以在不失一般性的情况下完成,因为只有 μ 之间的相对相位 和 ν 具有物理意义而不是它们的绝对相位。
从执行方程中的积分。 (22),我们有
$$ {\begin{aligned} \gamma_{G}(t) &=A_{0}^{2}\left[\left(\frac{\gamma^{2}}{4\Omega}+\Omega \right)t + \frac{g_{1}}{\Omega}\sin(\Omega t+2\varphi) \sin(\Omega t) +\frac{g_{2}}{\Omega} \cos (\Omega t+2\varphi) \right.\\ &\quad\left.\times\sin(\Omega t) {\vphantom{\frac{\gamma^{2}}{4\Omega}}} \right]\!-A_{0}\left[ \left(\frac{2m\Omega}{\hbar} \right)^{1/2}\omega X_{p,0} \bar{g}_ {3}(t) +\sqrt{\frac{2m}{\hbar\Omega}}\frac{1}{4\omega^{2}+\gamma^{2}}\bar{g}_{ 4}(t) \right]\\ &\quad+ \bar{g}_{5}(t) +\gamma_{G}(0), \end{aligned}} $$ (28)其中 \(\bar {g}_{i}(t)~(i=3,4,5)\) 由
给出 $$ \bar{g}_{i}(t) =G_{i}(t) -G_{i}(0), $$ (29)与
$$ {\begin{aligned} G_{3}(\tau) &=e^{\gamma \tau/2}\left(\frac{1}{4(\Omega+\omega)^{2}+\ gamma^{2}} \left\{2(\Omega+\omega)\sin[(\Omega+\omega)\tau+\varphi-\delta] \right.\right.\\ &\quad\left.+\ gamma \cos[(\Omega+\omega)\tau+\varphi-\delta] \right\}- \frac{1}{4(\Omega-\omega)^{2}+\gamma^{2}} \ { 2(\Omega-\omega) \\ &\quad\left.\left.\times\sin[(\Omega-\omega)\tau\,+\,\varphi\,+\,\delta]\ !+\gamma \cos[(\Omega-\omega)\tau\,+\,\varphi\,+\,\delta]\right\} {\vphantom{\frac{1}{4(\Omega+\ omega)^{2}+\gamma^{2}}}}\right),\\ \end{aligned}} $$ (30) $$ {\begin{aligned} G_{4}(\tau) &=e^{\gamma \tau/2} \left\{X_{p,0} \left\{ \gamma\omega[ 2\omega\cos(\omega \tau-\delta)-\gamma \sin( \omega \tau-\delta)] -2\omega_{0}^{2} \right.\right.\\ &\quad\left.\times[2\omega\sin(\omega \tau-\delta )+\gamma \cos(\omega \tau-\delta)] {\vphantom{X_{p,0}}}\right\}+2f_{\mathrm{d}} [ 2\omega\sin(\omega \tau) \\ &\left.\left.\quad+\gamma \cos(\omega \tau)\right]{\vphantom{X_{p,0}}}\right\}, \\ \end{对齐}} $$ ( 31) $$ {\begin{aligned} G_{5}(\tau) &=\frac{m\omega^{2}}{2\hbar}X_{p,0}^{2} \frac{e ^{\gamma \tau}}{\gamma \left(4\omega^{2}+\gamma^{2}\right)} \left\{ \gamma^{2}+4\omega^{2} -\gamma^{2} \cos[2(\omega\tau -\delta)]\right.\\ &\quad\left.-2\gamma\omega \sin[2(\omega \tau -\delta) )] {\vphantom{\gamma^{2}+4\omega^{2} -\gamma^{2}}}\right\} +\frac{\gamma^{2} \tau}{8\Omega }\left[2|\nu|^{2}-\left(\mu\nu+\mu^{*}\nu^{*}\right)+1\right] \\ &\quad+\frac{i \gamma \tau}{4(\mu-\nu)\left(\mu^{*}-\nu^{*}\right)} \left[|\mu|^{2}\left(\nu ^{2}-\nu^{*2}\right)-|\nu|^{2}\left(\mu^{2}-\mu^{*2}\right)\right.\\&\quad\left.+\left(2|\nu|^{2}+1\right)\left(\mu\nu^{*}-\mu^{*}\nu\right)\right]。 \end{对齐}} $$ (32)因此,我们已经评估了挤压状态下的完整几何相位,由方程给出。 (28) 与方程。 (23)、(24) 和 (29)-(32)。
几何相位的时间演变已在图 1 和图 2 中说明。 1、2、3 和 4。从图 1 中,我们看到几何相位振荡并且这种振荡的包络随时间增加。 A时包络的增加更大 0 很大。随着μ的值的增加,振荡模式逐渐变得不规则 和 ν 增加。而且,随着时间的推移,振荡幅度变大。
<图片>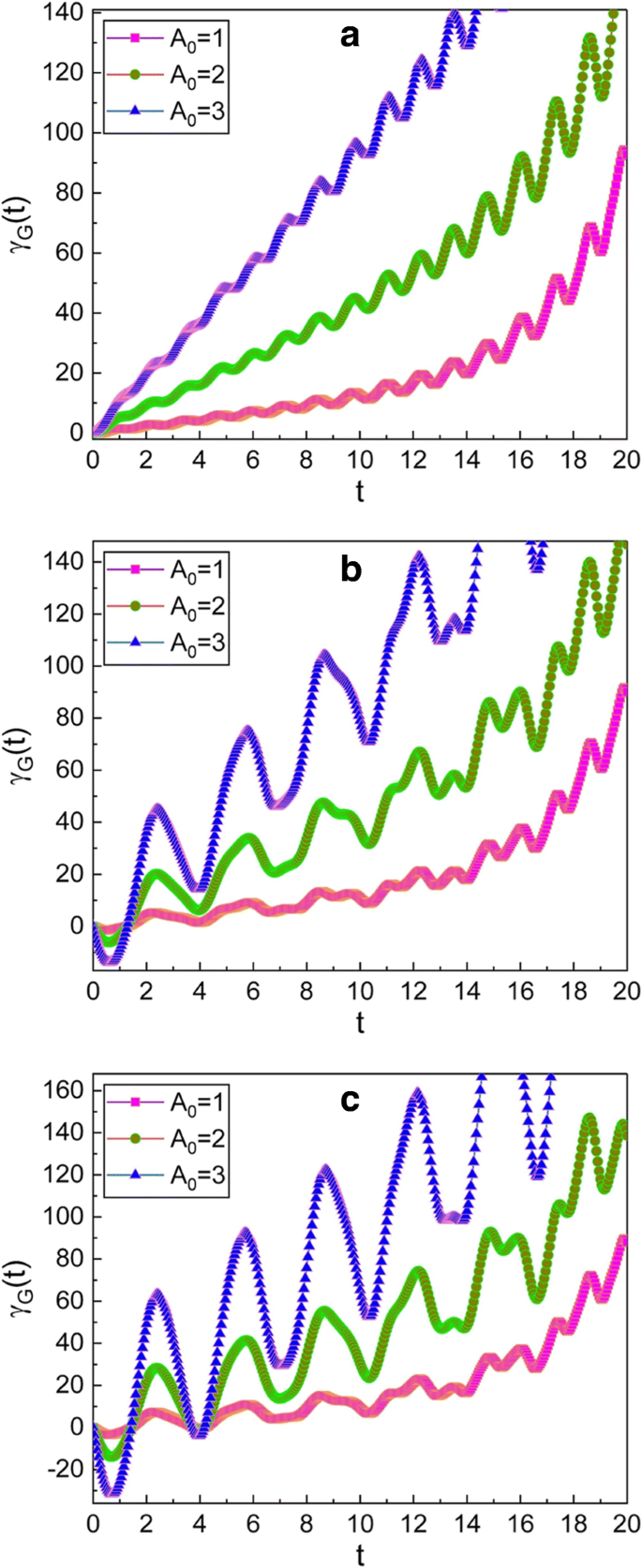
A 的几个不同值的几何相位的时间演化 0. (μ , ν ) 在图形中使用 (1, 0) 表示 a , (\(\sqrt {2}\), 1) 对于 b , 和 (\(\sqrt {3}\), \(\sqrt {2}\)) 对于 c .我们使用了 m =1,ω 0=1,ω =5, γ =0.35,f d=1, \(\hbar =1\), φ =0 和 γ G (0)=0。为方便起见,相位和所有参数均取为无量纲,此约定也将应用于后续图中。因为A 0 是根据经典振幅 X 给出的 c ,0 的互补函数 [见等式。 (12)],我们可以从图形中确认,当振荡幅度大时,几何相位大。我们还看到 γ 的波动 G (t ) 随着值 μ 变大 和 ν 在方程给出的条件下增加。 (14)
<图片>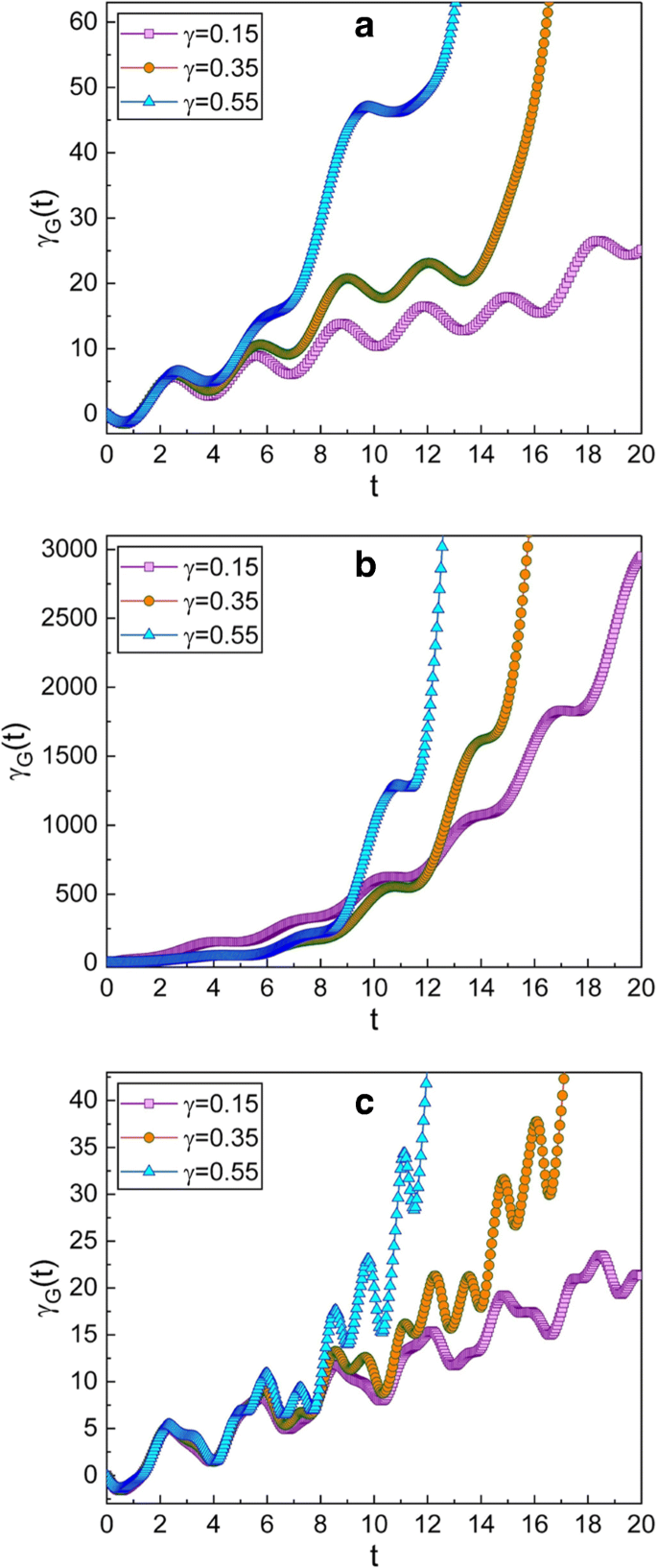
γ 的几个不同值的几何相位的时间演化 . ω 的值 图形中使用的 a 为 0.3 , b 为 0.99 , 5 表示 c .这里选择的挤压参数是\(\mu =\sqrt {2}\)和ν =1;这个选择给 q - 初始时的压缩状态。我们使用的其他数量是 m =1,ω 0=1,A 0=1,f d=1, \(\hbar =1\), φ =0 和 γ G (0)=0。我们确认当阻尼因子 γ 时几何相位很大 在大多数情况下很大,但不是全部。发生频率b 接近谐振频率,而 a 和 c 远不是共振的。谐振情况的几何相位 (b ) 随着时间的推移迅速增加
<图片>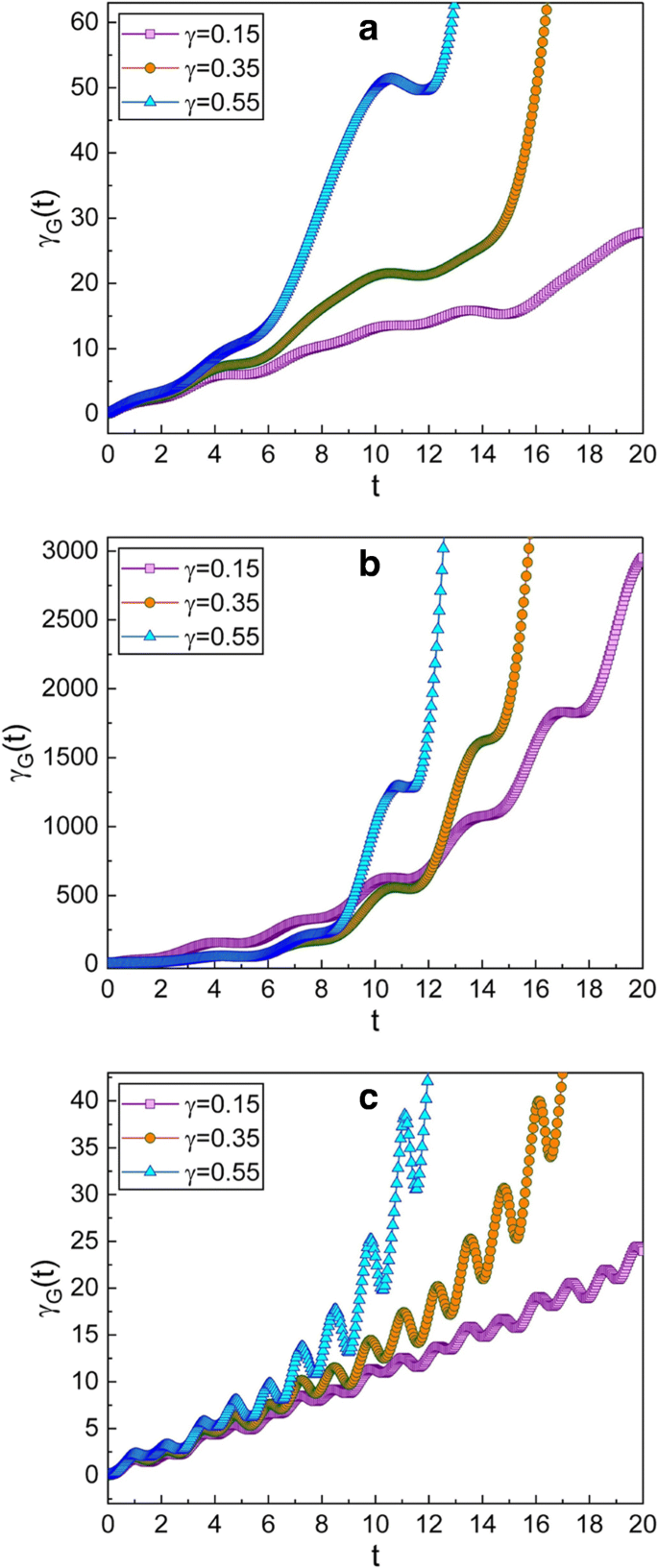
一 –c 该图形与图 2 相同,但对于所选挤压参数为 \(\mu =\sqrt {2}\) 和 ν 的情况 =−1 给出一个 p - 初始时的压缩状态。从这种情况下的整体图形与图 2 中对应的图形没有太大不同,我们可以确认 γ 的演化 G (t ) 几乎与挤压类型无关,只要 μ 的绝对值 和 ν 不改变
<图片>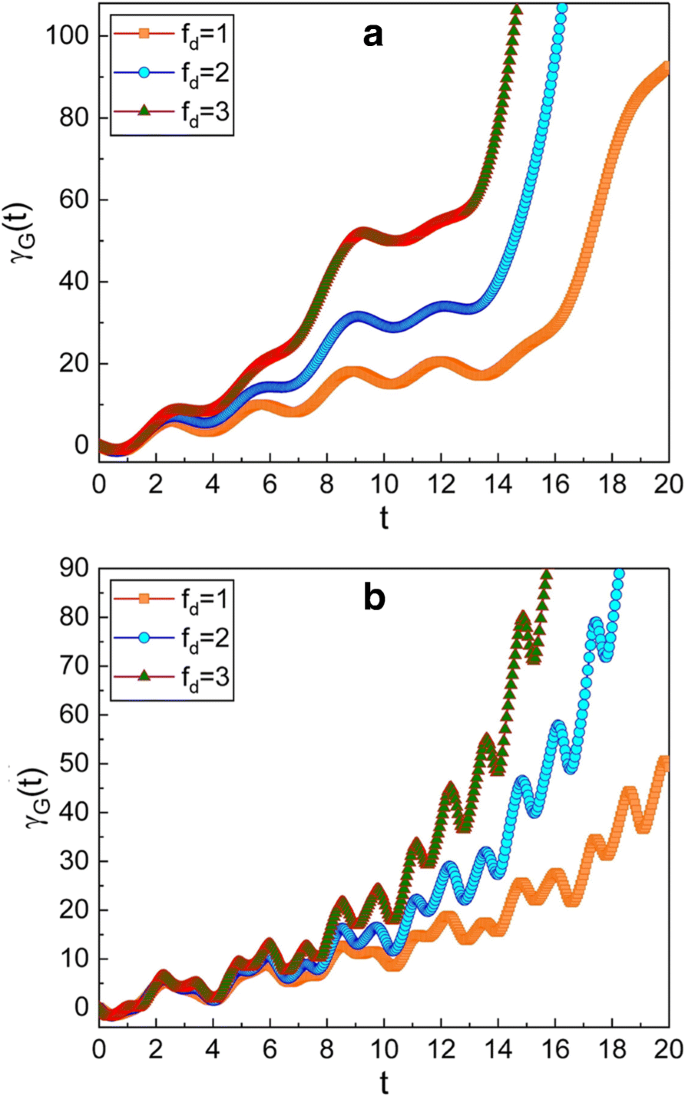
f 的几个不同值的几何相位的时间演化 d. ω 的值 图形中使用的 a 为 0.3 b 为 5 .我们使用了 \(\mu =\sqrt {2}\), ν =1,米 =1,ω 0=1,γ =0.3,A 0=1, \(\hbar =1\), φ =0 和 γ G (0)=0。由于振幅 (f d) 驱动力增大,几何相位变大
挤压状态下的挤压效果取决于挤压参数 c 其中 c =μ /ν 已在参考文献中进行了调查。 [39]。根据参考文献中给出的分析。 [39](参见参考文献 [39] 中的图 1(a)),图 2 所示的挤压状态对应于 \(c=\sqrt {2}\),是 q -squeezed 初始状态,而图 3 中对应于 \(c=-\sqrt {2}\),是 p - 在相同情况下的挤压状态。通过比较图。 2 和 3 相互结合,我们可以得出结论,q 中的几何相位 -squeezed 状态几乎与 p 中的状态相同 -挤压状态。
γ的影响 几何相位的演变可以从图 2 中得到证实。 2和3.当γ时几何相位增加得更快 很大。通过比较图。 2a 和 3a 与图。由图 2c 和 3c 可知,当 ω 大于谐振角频率。
几何相位在系统谐振状态或附近的时间行为可能会引起人们极大的兴趣 [22, 23]。图 2b 和 3b 表明,当 ω 时,几何相位增加得非常快。 接近共振角频率。这意味着这种情况下的波函数随时间变化很大,因为几何相位的大小与波函数的时间变化有关。事实上,导线振荡的振幅在共振状态下显着增加。顺便说一下,悬浮的基于 CNT 的纳米线谐振器的谐振角频率不仅很高,而且还可以通过非常高质量的因素进行广泛调谐 [3]。为此,系统的振动模式将保持很长时间,直到它们完全衰减[11]。
图4表明几何相位也受驱动力f幅值的影响 d.作为 f d 增大,几何相位随时间增加较快。
结论
我们基于量子动力学和薛定谔方程研究了系统在压缩状态下的几何相位。关于描述系统的哈密顿量的时间相关性,引入了不变算子方法,这是在用时间描述哈密顿量的情况下推导量子解的潜在工具。利用该方法得到了碳纳米管基纳米线振荡几何相位的解析公式。
已经进行了对相位效应的详细分析,这是对机械振动的理论理解所必需的。我们对几何相位的开发是完全基于量子的,具有严格的数学评估。几何相位对机械参数的变化很敏感,并且在很多情况下表现出振荡。还分析了挤压参数对几何相位演变的影响。我们已经证实,随着时间的推移,在谐振角频率附近几何相位积累有很强的增加。
我们的结果说明了出现在基于 CNT 的纳米线的振动中的几何相位的时间特性。在这项工作中给出的几何相位分析不仅对于理解系统的拓扑特征很重要,而且对于理解其他基于纳米线的机械振荡器的动态振动也很重要。特别是,我们已经开发了共振态的相位特性,在系统在量子信息技术和其他基于量子的行业中的应用中需要对其进行澄清 [40]。本研究中使用的类似方法和框架也可以扩展到其他纳米系统,例如超导法布里-珀罗谐振器[41]、纳米悬臂梁[42]和量子位-谐振器-原子混合系统[43]。
缩写
- CNT:
-
碳纳米管
- 电磁波:
-
电磁波
- TDHS:
-
时变哈密顿系统
纳米材料


