捕集系统中准单分子和等离子体腔之间的强耦合

介绍

近年来，使用光学偶极子陷阱来捕获和冷却原子或分子已成为实现玻色-爱因斯坦凝聚、测试基本物理定律和更精确地测量基本物理常数的一项有前途的技术 [1-3]。光偶极阱主要利用入射光的梯度力在原子上产生偶极效应。对于红失谐陷阱，原子被困在吸引力潜力下光强度最强的位置[4]。由于瑞利和拉曼散射，被捕获的原子将受到明显的原子相干和加热效应。同时，在最强光位置，核能级有严重的光频移[1]。相反，对于蓝色失谐陷阱 [5, 6]，原子被困在排斥电位下光强度最弱的区域 [6-8]。与红失谐陷阱相比，光子的散射率可以在入射光强度较弱的情况下显着降低，因此提供了一种更稳定的捕获小粒子的方法。然而，蓝失谐陷阱的构建通常很复杂 [9, 10]。表面等离子体激元 (SPP) 是光波的混合模式，耦合到限制在电介质和金属之间界面处的自由电子振荡，在太赫兹器件领域具有广泛的应用潜力 [11-14]，材料 [15]、传感器 [16]、超表面 [17] 和量子信息处理 [18]。将光捕获与等离子体结构相结合是开发集成光学组件的可能性。例如，Chang 等人。建议使用具有组合纳米尖端和微盘腔的纳米结构来捕获孤立的原子 [19]；陈等人。基于等离子体纳米孔阵列中的蓝光失谐光实现了稳定的 3D 原子捕获 [20]。具有亚波长孔阵列的周期性等离子体纳米结构具有有趣的光学性质，这是捕获原子或分子等小粒子的令人鼓舞的场景。

等离子体腔与分子之间的强耦合不仅引起了量子电动力学现象基础研究的兴趣，而且在量子信息处理中也具有广阔的前景[21-23]。等离子体腔可以显着增强光-物质相互作用的强度，是在室温下实现强耦合的合适候选[24-26]。然而，单分子与等离子体腔的耦合在理论和实验上都是一个巨大的挑战，很难操纵分子在耦合系统中的位置。

在本文中，我们从理论上研究了蓝色失谐捕获系统每个单元的准单分子与等离子体腔之间的强耦合。蓝色失谐捕获系统由金纳米孔阵列组成，每个单元仅捕获一个分子。采用时域有限差分(FDTD)方法对我们的结构进行模拟，得到透射谱。当分子被困在最弱点时，散射光谱表现出 Rabi 分裂，这是强耦合机制的特征。所提出的结构为实现光捕获系统中准单分子与等离子体腔之间的强耦合提供了一种潜在的途径。

方法

我们设计了一个周期性的纳米孔结构来实现蓝色失谐捕获。我们的模拟基于 FDTD 方法，我们采用 EAST FDTD 软件来设置我们的结构并研究传输频谱和电磁分布。在我们的模型中，一系列半径为 R 的金纳米孔单元排列在 X 中的二维 (2D) Au 膜中 -是 平面，Au 膜的厚度为 400 nm。晶格常数L 和半径 R 分别为 1000 nm 和 250 nm。在我们的模拟过程中，背景指数为 1，每个方向的网格为 5 nm。沿 X 设置周期性边界条件 -axis 和 Y -轴。完美匹配层沿Z设置 -轴。完美匹配层的数量为 32。Au 的介电常数是从 Johnson 和 Christy 获得的 [27]。圆偏振光通常沿 Z 注入到所建议结构的表面上 轴，波长为 696 nm。 X -是 平面记录器距离建议的结构表面 400 nm 以计算透射率和 X -Z 平面记录仪位于结构中心，以获取电磁场分布。由于FDTD模拟中偶极子源的特性[28-30]，我们可以使用偶极子源来模拟分子。分子共振波长为707 nm，衰减率为1.1×10 ¹⁴ 赫兹。在我们的模拟中，传输 T 通过对上表面的坡印廷矢量进行积分并归一化为在没有金属结构的情况下获得的矢量 [31] 来计算。 FDTD模拟计算的透射率表示为T =我 T /(我 C +我 D )，其中 I T 是传输的电磁场强度，I C 是圆偏振光的电磁场强度，I D 是偶极子的电磁场强度。

结果与讨论

诱捕结构

具有亚波长孔阵列的等离子体纳米结构表现出非凡的光传输效应，这将显着增强纳米孔附近的局部电场 [32-34]。我们将这种效应用于分子运动。当等离子体共振场与分子共振发生蓝色失谐时，会产生巨大的分子排斥力，并且会在距结构表面约数百纳米的地方产生最小俘获。我们设计了一个周期性的等离子体纳米结构来展示我们的方法，如图 1 所示。

周期性等离子体纳米结构示意图

在本节中，我们只讨论没有分子的模拟结果。我们使用圆偏振光从 Z 正常照亮结构 无穷远方向，透射光谱如图2所示。

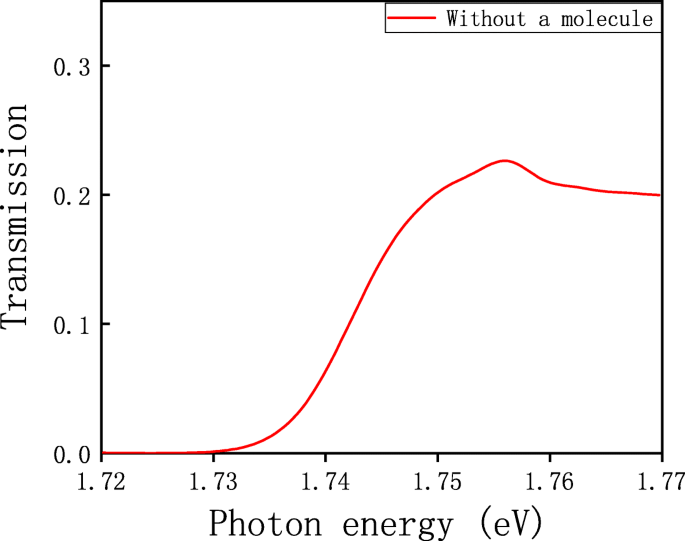
无分子结构的透射光谱

在 707 nm (1.756 eV) 处观察到共振峰，它源于单元（空穴）之间的相互作用。该峰值接近伍德异常 [35] 的 (1, 1) 阶波长。亚波长孔阵列对 SPP 具有布拉格散射，从而产生阵列的倒易晶格矢量，可以轻松满足相位匹配条件 [20]。因此，入射光可以激发 SPP，这种激发 SPP 的方式比使用 Kretschmann 结构容易得多，并且不受金属厚度的影响。为了研究系统的空间电磁场分布，我们绘制了|E | ² X 的分布 -Z Y 处的平面 =0 在 707 nm 的谐振波长处，如图 3a 所示。

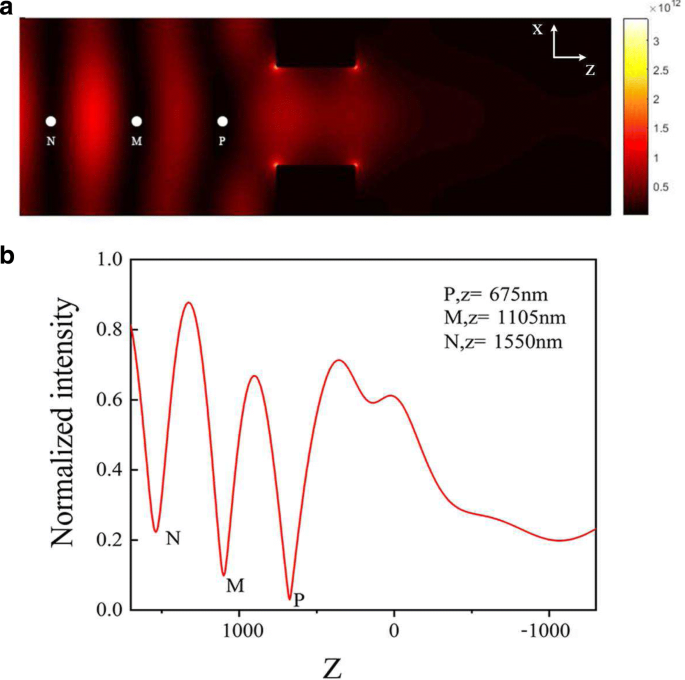
一 电磁场强度|E | ² X 中的分布 -Z Y 处的平面 =0 在 λ =696 纳米。 b |E 的归一化强度分布 | ² 对比 Z 与 X =0 和 Y =0 在 X -Z 飞机

在图 3a 中，|E 有三个最小值 | ² 由白点 P、M 和 N 表示；这三个最小值的出现可归因于热点的出现，这是由一系列等离子体纳米孔对光的近场散射造成的。实际上，电磁场的分布是通过纳米孔的表面等离子体场和空间电磁场的叠加。 |E 的曲线 | ² 对比 Z 在 X =0 和 Y =0 在 X -Z 平面也绘制在图 3b 中。根据空间电磁分布的模拟结果，将有三个强度最小值，这意味着蓝光失谐光阱。

分子可以通过光学偶极力和蓝色失谐光被困在电磁场强度最小值中。在我们的模拟中，分子被视为两能级系统，并且可以在 FDTD 模拟中模拟为偶极子 [28-30]。诱捕势 U 选择分子是与电磁场相关的排斥性光学偶极子势E , 由 [1, 4] 给出：

这里，α 极化率降低，在我们的例子中 α =−7.8​​7×10 ⁻³⁸ F ·米 ² [20]。因此，根据电磁场强度分布，我们可以得到俘获势。使用方程。 (1) 和 |E | ² 在图 3a 中的分布中，我们计算了沿 X 线的捕获电位 =0 和 Y =0，如图 4 所示。

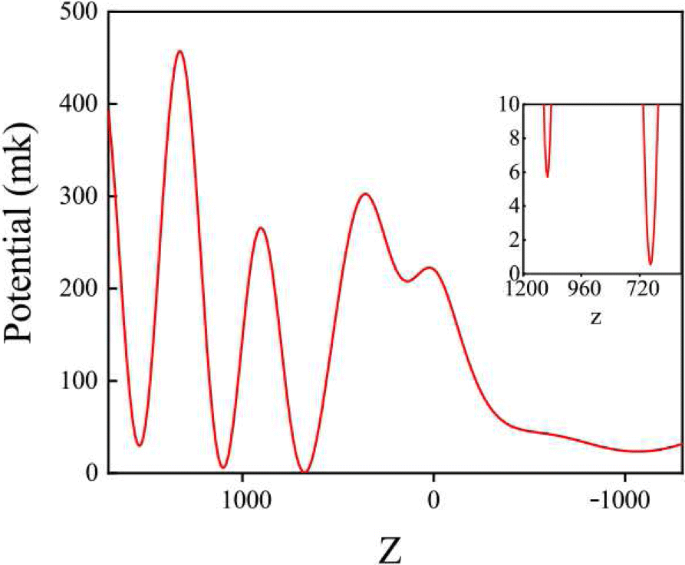
在 X 中捕获潜力 -Z Y 处的平面 =0.插入图片是最低诱捕电位的放大

在图 4 中，我们知道最低强度位置在 P 点。这里，入射功率设置为 P 我 =120 mW，捕获电位为 0.53 mK。陈等人。已报告 ⁸⁷ R b 可以用 2.02 mK 的捕获电位稳定捕获 [20]。比较这些参数，我们的蓝失谐捕获系统可以捕获一个分子量约为 400 的罗丹明分子。根据上面的分析，我们选择在点 (0, 0, 675 nm) 处的捕获位置，示意图被困在结构中的分子示意图如图 5 所示。

分子被困在结构中的示意图

结构和分子之间的强耦合

分子被放置在我们结构的每个单元中，以研究强耦合状态下的光分子相互作用。在 FDTD 模拟中，可以将分子视为偶极子。我们在距离表面 275 nm 的潜在最小点 P 添加一个偶极子，如图 3a 所示。偶极子的极化可以沿着 X -axis，Y -axis，或 Z -轴。分子的共振波长为 707 nm (1.756 eV)。首先，我们考虑偶极子沿 Z 的极化 -轴。还得到了透射光谱，结果如图 6 所示。

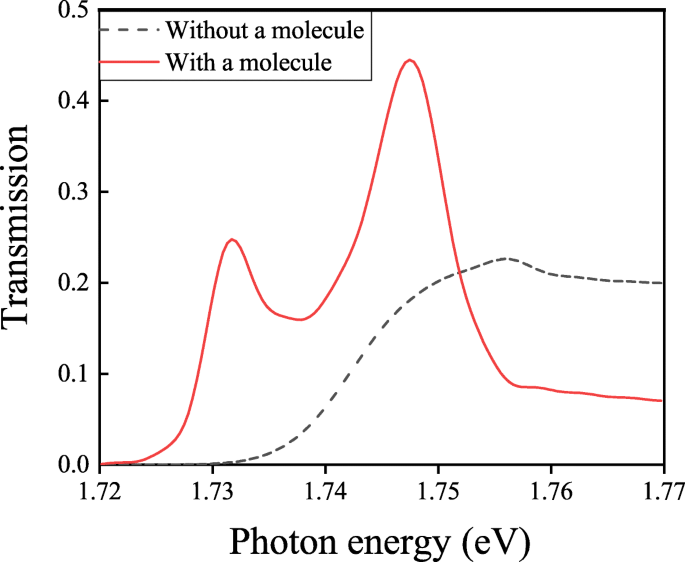
有分子和无分子的透射光谱被困在 P 点

为了比较，图6还绘制了每个单元中没有分子的结构的透射光谱。与图6一致，我们可以在有分子的结构的透射光谱中观察到两个分裂峰，这表明Rabi分裂线形并呈现强耦合现象。入射光不仅射入我们的结构表面，而且使分子被激发。由入射光激发的 SPP 与由工作波长附近的分子激发的 SPP 耦合。这两种 SPP 相互耦合并在透射光谱中形成两个分裂峰。传输曲线的线型显示出强耦合现象。一般来说，这两个分裂峰的频率 ω ±表示为[36, 37]：

其中 ω 0 是假设孤立分子和空腔共振条件下的能量，γ c =4.08×10 ¹³ 赫兹 [38] 和 γ 米 =1.1×10 ¹⁴ Hz 分别是等离子体腔和分子的衰减率，g 是耦合常数。 g 发生强耦合>0.5|γ c -γ 米 |并且对应于具有有限寿命的修整状态的形成。对于我们提出的结构，耦合常数 g 是 144 meV，而 0.5|γ c -γ 米 |是 143 meV。在以前的工作中，Rabi分裂表示为Ω =|ω +−ω -|在基于 J 聚集体-金属或分子-金属混合纳米结构的结构中，在 100 到 450 meV 的范围内 [39, 40]。 Rabi分裂与耦合强度g有关 ，这取决于\(\sqrt {N/V}\)，其中 N 是分子数和V 分别是模式音量 [37]。在我们的工作中，所提出结构的每个单元中只有一个分子，模式体积 V 大到 Rabi 分裂 Ω 约为 16 meV，这种分裂与金属-半导体混合纳米结构 [41] 和金属-二维材料系统 [42] 中的强耦合相当。我们还研究了结构与分子沿 X 极化的强耦合 -axis 和 Y - 轴，分别。仿真结果如图 7 所示。

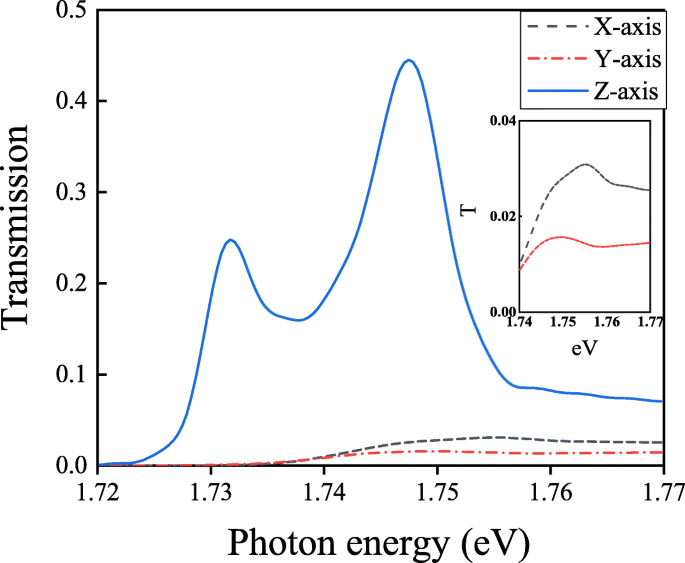
分子分别沿 X、Y 和 Z 方向偏振的透射光谱

在图 7 中，两个分裂峰（710 nm，1.747 eV；717 nm，1.717 eV）仅出现在分子沿 Z 极化的结构中 -轴。分子沿 X 极化 -axis 或 Y -轴在与 Au 纳米腔或 Au 纳米孔阵列耦合之前显示出强烈的集体行为。集体行为S k 沿 X 极化的分子 -axis 或 Y -轴可以通过耦合偶极子方法计算[43]：

其中 k 0 是真空中的波矢，θ 是两个偶极子之间的夹角，r =n L , n =1, 2, 3... 这里，条件为 \( \lambda =\frac {L}{\sqrt {i^{2}+j^{2}}}\) (i , j =0, 1, 2,..., 但都是 i 和 j 不等于 0），集体行为是相当大的，这在 Eq. (3) [35, 43]。它在透射光谱中表现出共振下降。对于沿 X 极化的分子 -axis 或 Y 轴，集体行为太大而无法削弱分子与等离子体腔之间的耦合。我们只看到波长707 nm（1.756 eV）附近的透射光谱中Wood异常[35]的阶次为（1, 1），强耦合无法出现。因此，只有沿 Z 极化的分子 我们提出的结构中的 -axis 可以产生强耦合现象。如果改变分子的共振波长，也可以通过以下步骤获得蓝失谐捕获系统中的强耦合。首先，根据分子的共振，可以固定纳米孔阵列的晶格常数。其次，还可以确定蓝色失谐捕获系统的工作波长，这取决于金属纳米孔阵列的晶格常数。第三，获得电磁场分布以找到诱捕位置。最后，将分子置于最佳捕获位置计算透射谱，得到强耦合线形的透射。

结论

总之，我们设计了一种金属等离子体蓝失谐捕获系统，并研究了准单分子与捕获系统之间的强耦合现象。在FDTD模拟中，我们使用偶极子源作为分子，根据电磁场分布，我们可以找到在结构中仅捕获单个分子的最佳位置。通过计算分子被困与否时所提出结构的透射率，我们发现当分子被困在结构中时，透射光谱中有两个分裂峰，而当分子未被困时，只观察到一个峰.两个分裂峰表明发生了强耦合。因此，我们可以设计蓝色失谐捕获系统以实现纳米等离子体结构中的强耦合，这在量子信息处理中具有潜在的应用。

缩写

FDTD：

有限差分时域