负二进制数

由于加法很容易完成，我们可以使用相同的技术简单地通过将其中一个数字设为负数来执行减法运算。例如，7-5的减法问题与7+(-5)的加法问题本质上是一样的。

既然我们已经知道如何用二进制表示正数，那么现在我们只需要知道如何表示它们的负数，我们就可以做减法了。

通常我们通过在最高有效数字的左侧直接放置一个减号来表示负十进制数，就像上面的例子一样，用 -5。然而，使用二进制符号的全部目的是构建可以用电压表示位值的开/关电路（2 个替代值：“高”或“低”）。

在这种情况下，我们没有像“减号”这样的第三个符号的奢侈，因为这些电路只能打开或关闭（两种可能的状态）。一种解决方案是保留一个位（电路），它只表示数学符号：

如您所见，当我们开始将位用于标准位置加权值以外的任何目的时，我们必须小心。否则，11012 可能会被误解为数字 13，而实际上我们的意思是表示负 5。

在这里，为了使事情简单明了，我们必须首先决定需要多少位来表示我们将要处理的最大数字，然后确保在我们的算术运算中不要超过该位字段长度。

对于上面的示例，我将自己限制为从负七 (11112) 到正七 (01112) 的数字表示，仅此而已，将第四位设为“符号”位。只有首先建立这些限制，我才能避免将负数与更大的正数混淆。

将负五表示为 11012 是负二进制数的符号大小系统的一个示例。通过使用最左边的位作为符号指示符而不是位置加权值，我牺牲了二进制表示法的“纯”形式，以获得实际优势：负数的表示。

最左边的位被读取为正负号，其余位根据标准二进制表示法进行解释：从左到右，将权重置于 2 的倍数。

补充

尽管符号幅度方法很简单，但它对于算术目的来说并不是很实用。例如，如何使用二进制加法的标准技术将负五 (11012) 添加到任何其他数字？

我必须发明一种新的加法方法才能让它发挥作用，如果我这样做，我还不如用普通的减法来完成这项工作；如果我们必须使用符号幅度计算，那么使用负数通过加法执行减法没有算术优势，这就是我们的目标！

还有另一种表示负数的方法，它适用于我们的熟悉的普通加法技术，而且从位置加权计数的角度来看也更有意义，称为补码。

使用这种策略，我们将最左边的位分配给特殊用途，就像我们使用符号大小方法所做的那样，就像以前一样定义我们的数量限制。然而，这一次，最左边的位不仅仅是一个符号位；相反，它具有负的位置权重值。例如，负 5 的值将表示为：

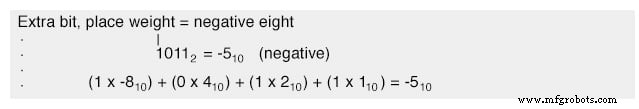
右边三位能够表示从零到七的幅度，最左边的位表示零或负八，我们可以成功地表示从负七 (10012 =-810 + 12 =-710) 到正的任何整数七 (01112 =010 + 710 =710).

在这个方案中表示正数（第四位指定为负权重）与普通二进制表示法没有什么不同。然而，表示负数并不那么简单：

请注意，右列中的负二进制数，即右三位的总和加上最左位的负八位之和，与左列中的正二进制数不以相同的级数“计数”。

相反，当与最左边位的负八位值相加时，必须将右边的三位设置为适当的值以等于所需的（负）总数。

补码

那些右边的三位被称为相应正数的二进制补码。考虑以下比较：

在这种情况下，负权重位是第四位（负八的位置值），任何正数的二进制补码将是需要添加到负八以使该正值的负等效的任何值。

值得庆幸的是，有一种简单的方法可以计算任何二进制数的二进制补码：简单地反转该数字的所有位，将所有 1 更改为 0，反之亦然（得出所谓的补码），然后加一！例如，要获得五的二进制补码（1012），我们首先将所有位取反得到 0102（“一个的补码”），然后加一得到 0112，或 -510 的三位二进制补码形式

有趣的是，如果您操作所有位，包括最左边（符号）位和幅度位，则生成二进制数的二进制补码的工作方式相同。让我们用前面的例子试试这个，将正五转换为负五，但对所有四位执行补码过程。

我们必须确保在原始数字五 (01012) 中包含 0（正）符号位。首先，将所有位取反得到一个的补码：10102。然后，加一，我们得到最终答案：10112，或-510，以四位二进制补码形式表示。

很关键重要的是要记住，在进行任何二进制补码转换之前，必须已经确定负权重位的位置。如果我们的二进制数字字段将第八位指定为负权位 (100000002)，我们就必须根据所有其他七位来确定二进制补码。

这里，五的二进制补码 (00001012) 将是 11110112。本系统中的正五表示为 000001012，负五表示为 111110112。

相关工作表：

• 二进制数学工作表