复数的极坐标形式和矩形形式符号

为了在不绘制向量的情况下处理复数，我们首先需要某种标准的数学符号。复数符号有两种基本形式：polar 和矩形 .

复数的极坐标形式

极坐标形式是复数由长度表示的地方 （也称为幅度 , 绝对值 , 或 模数 ) 和 角度 其向量的（通常用如下所示的角度符号表示：∠）。

使用地图类比，从纽约市到圣地亚哥的矢量的极坐标表示法类似于“西南 2400 英里”。以下是向量及其极坐标符号的两个示例：

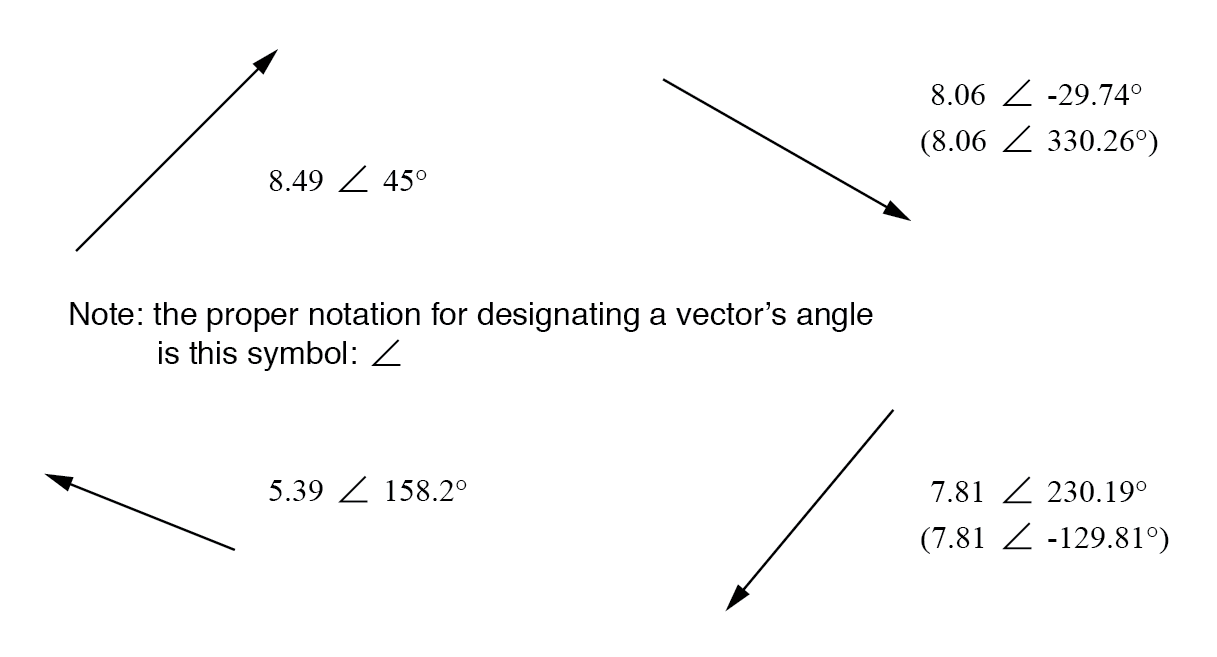
带有极坐标符号的矢量。

交流电路计算中矢量角的标准方向将 0° 定义为向右（水平），即向上 90°、向左 180° 和向下 270°。请注意，“向下”角度的矢量的角度可以以极坐标形式表示为超过 180 的正数，或小于 180 的负数。

例如，角度为∠ 270°（直线向下）的向量也可以说具有-90°的角度。 （下图）上面右边的向量（7.81 ∠ 230.19°）也可以表示为7.81 ∠ -129.81°。

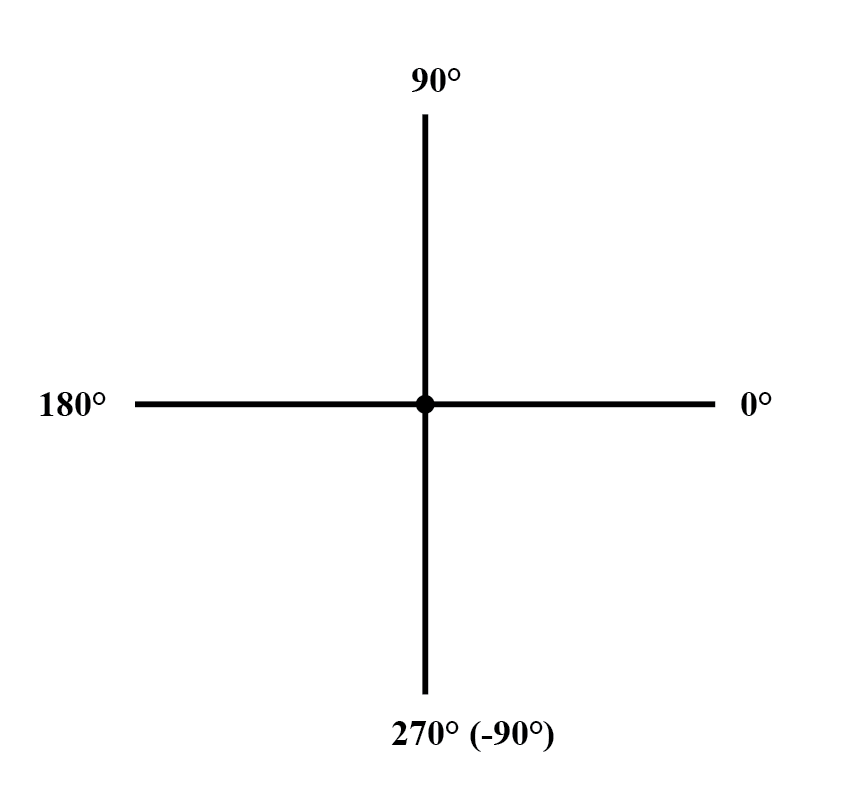
矢量罗盘。

复数的矩形形式

另一方面，矩形形式是复数由其各自的水平和垂直分量表示的地方。本质上，角度向量被认为是直角三角形的斜边，用相邻和对边的长度来描述。

不是通过表示大小和角度来描述矢量的长度和方向，而是用“向左/向右多远”和“向上/向下多远”来描述。

这些二维图形（水平和垂直）由两个数字图形表示。为了区分水平和垂直维度，垂直以小写字母“i”（纯数学）或“j”（电子学）作为前缀。

这些小写字母不代表物理变量（如瞬时电流，也用小写字母“i”表示），而是数学运算符 用于区分向量的垂直分量和水平分量。作为一个完整的复数，水平和垂直量写成和：（下图）

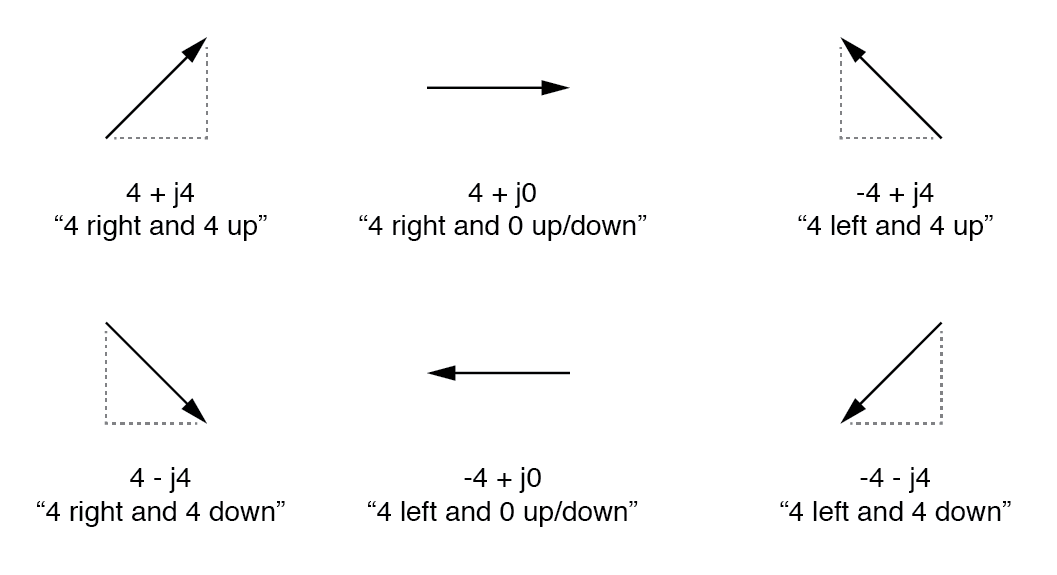
在“矩形”形式中，向量的长度和方向用其水平和垂直跨度表示，第一个数字表示水平（“真实”），第二个数字表示数字（带有“j”前缀）代表垂直（“虚数”）维度。

水平分量被称为 real 组件，因为该维度与正常的标量（“实数”）数兼容。垂直分量被称为虚部 分量，因为该维度位于不同的方向，与实数的规模完全不同。 （下图）

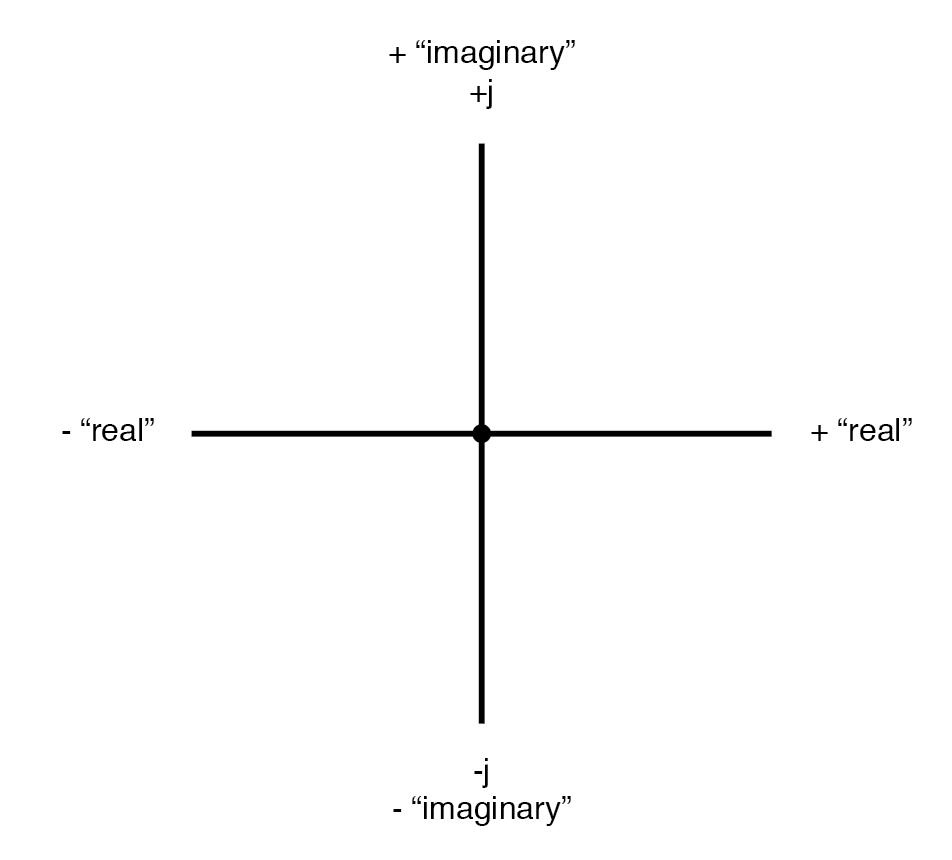
矢量罗盘显示实轴和虚轴。

图的“实”轴对应于我们之前看到的熟悉的数轴：上面有正值和负值的数轴。图中的“虚”轴对应于与“实”轴成 90° 的另一条数轴。

向量是二维的东西，我们必须有一个二维的“地图”来表达它们，因此两条数轴相互垂直：（下图）

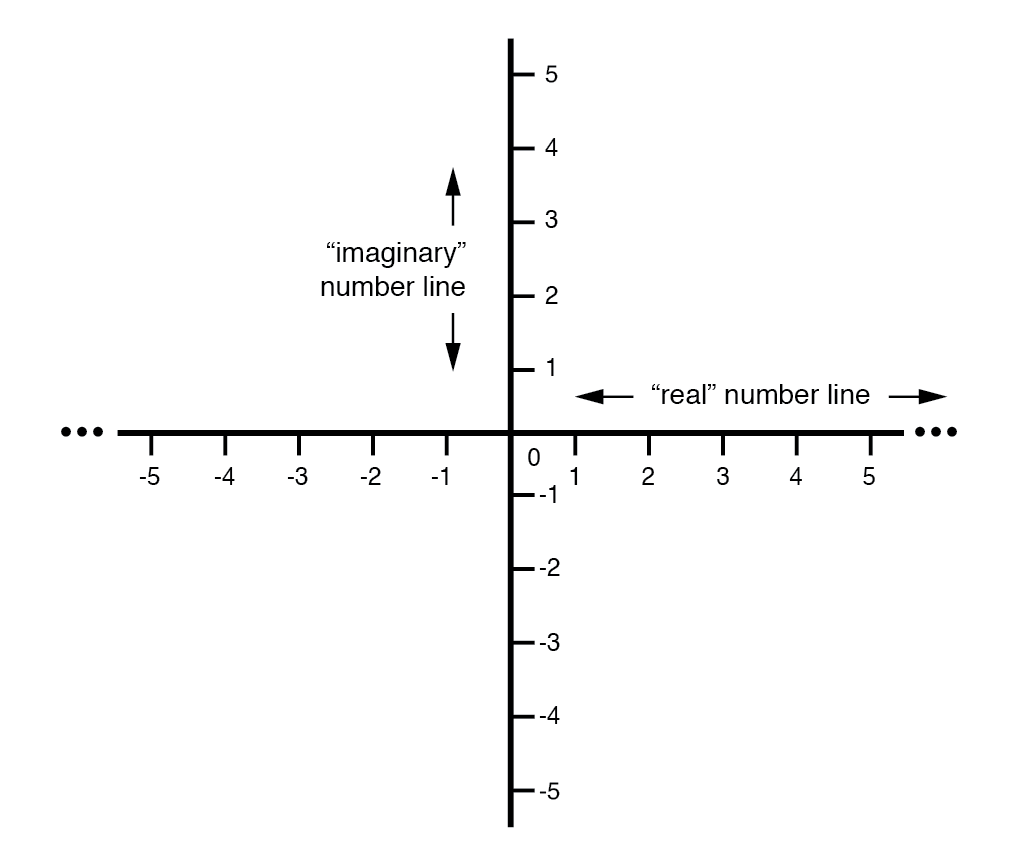
带有实数和虚数 (“j”) 数轴的矢量罗盘。

从极坐标形式转换为矩形形式

两种表示法都适用于复数。有两种记法的主要原因是为了便于计算，矩形适合加减法，极坐标法适合乘除法。

两种符号形式之间的转换涉及简单的三角学。要从极坐标转换为矩形，通过将极坐标值乘以角度的余弦值来求实分量，通过将极值值乘以角正弦值来求虚分量。

通过将数量绘制为直角三角形的边，三角形的斜边代表向量本身（其长度和相对于水平线的角度构成极坐标形式），水平和垂直边代表“分别为实数和虚数矩形分量：（下图）

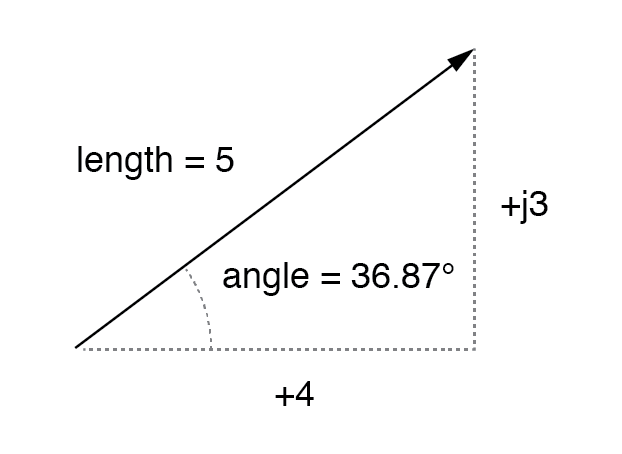
根据实部 (4) 和虚部 (j3) 分量表示的幅度向量。

从矩形转换为极坐标

将矩形转换为极坐标，通过使用勾股定理求极坐标大小（极坐标大小为直角三角形的斜边，实部和虚部分别为邻边和对边），角为取虚部除以实部的反正切：

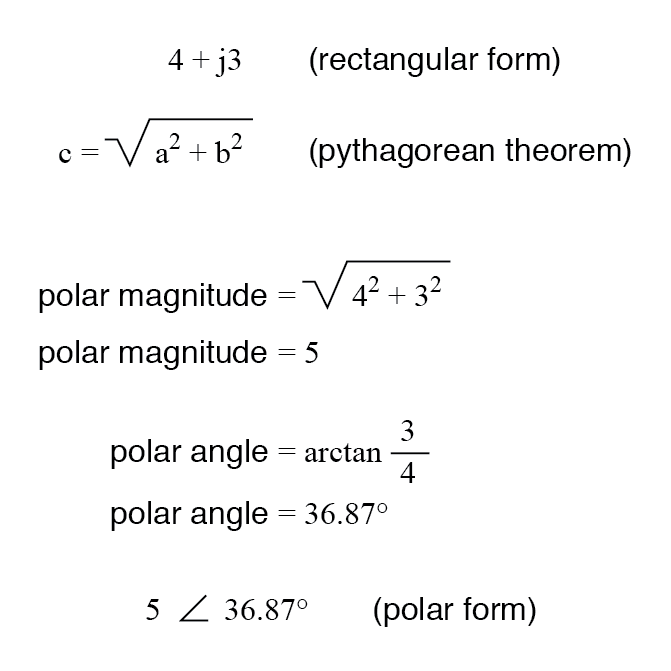
评论：

• 极地 符号表示一个复数，表示其向量的长度和从起点的角度方向。示例：飞行 45 英里 ∠ 203°（西南偏西）。
• 矩形 符号表示一个复数的水平和垂直维度。示例：向西行驶 41 英里，然后转向向南行驶 18 英里。
• 在矩形符号中，第一个量是“实数”分量（向量的水平维度），第二个量是“虚数”分量（向量的垂直维度）。虚部前面有一个小写的“j”，有时称为 j 运算符 .
• 复数的极坐标和矩形符号都可以以直角三角形的形式图形相关，斜边代表向量本身（极坐标形式：斜边长度 =幅度；相对于水平边的角度 =角度)，水平边代表矩形“实”分量，垂直边代表矩形“虚”分量。

相关工作表：

• 交流阶段工作表