复数算术
由于复数是合法的数学实体,就像标量一样,它们可以加、减、乘、除、平方、倒数等,就像任何其他类型的数字一样。
一些科学计算器被编程为直接对两个或更多复数执行这些运算,但这些运算也可以“手动”完成。本节将向您展示如何执行基本操作。
这是高度 建议您配备一个能够轻松对复数执行算术运算的科学计算器。与被迫长时间进行所有计算相比,这将使您对交流电路的研究更加愉快。
矩形复数的加减法
矩形复数的加减法很容易。对于加法,只需将复数的实部相加即可确定和的实部,将复数的虚部相加即可确定和的虚部:
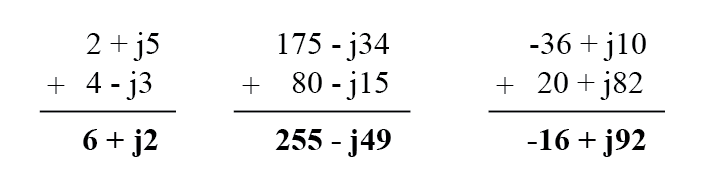
以矩形形式相减复数时,只需将第一个复数的实部减去第一个复数的实部即可得到差值的实部,然后将第二个复数的虚部减去第二个复数的虚部最先到达差值的虚部:
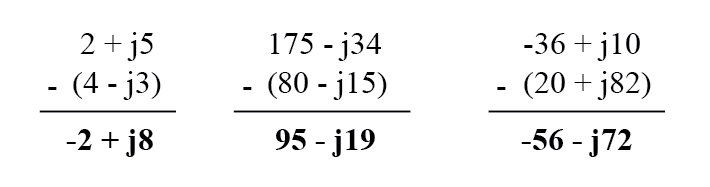
极坐标形式复数的乘法和除法
对于普通乘法和除法,极坐标是最常用的符号。以极坐标形式乘以复数时,只需乘以 复数的极坐标确定乘积的极坐标,然后相加 复数的角度来确定乘积的角度:
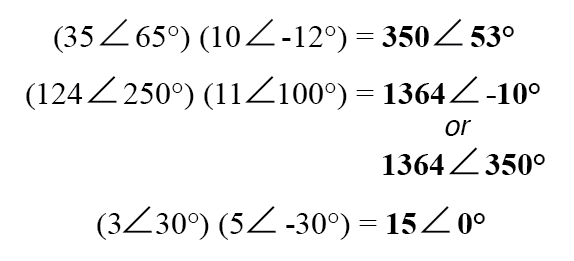
极坐标复数的除法也很简单:只需将第一个复数的极坐标除以第二个复数的极坐标即可得到商的极坐标,然后减去第二个复数的角度到达商角的第一个复数的角:
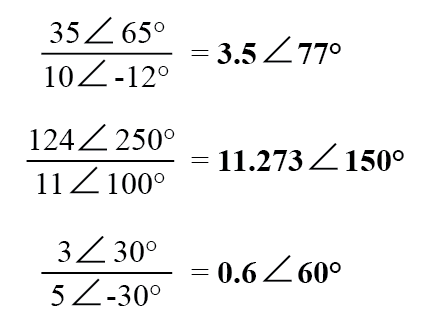
要获得复数的倒数或“倒数”(1/x),只需将该数(以极坐标形式)除以标量值 1,该标量值只不过是一个没有虚部的复数(角度 =0):
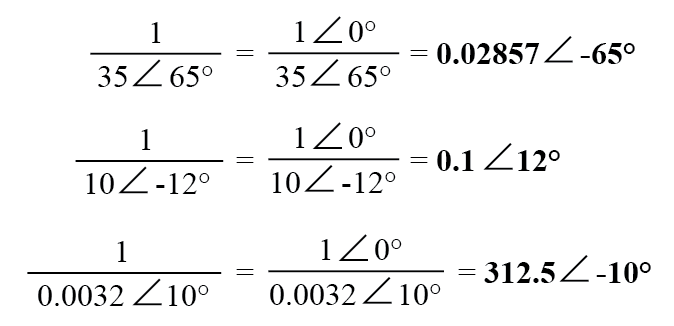
这些是您需要了解的基本操作,以便在交流电路分析中操作复数。然而,复数运算绝不仅限于加、减、乘、除和求逆。
几乎任何可以用标量完成的算术运算都可以用复数完成,包括幂、根、用复系数求解联立方程,甚至三角函数(尽管这涉及三角学的全新视角,称为双曲函数 这远远超出了本讨论的范围)。
一定要熟悉加减乘除的基本算术运算,交流电路分析不会有什么问题。
评论:
- 要以矩形形式添加复数,请添加实部并添加虚部。减法类似。
- 要以极坐标形式乘以复数,请乘以幅度并加上角度。要进行除法,请将大小相除,然后从另一个角度减去一个角度。
相关工作表:
- 交流阶段工作表
工业技术


