补偿定理——证明、解释和解决的例子

电路分析补偿定理的证明、解释、实验和求解示例

补偿定理

在网络理论中，了解或研究其分支中阻抗变化的影响非常重要。它会影响网络或电路的相应电压和电流。补偿定理给出了网络变化的信息。

补偿定理适用于欧姆定律的基本概念。根据欧姆定律，当电流通过电阻器时，电阻器上会出现一定量的电压降。这个电压降将与源电压相反。

因此，我们连接了一个与源电压相反极性的额外电压源，并且幅度等于电压降。补偿定理适用于这个概念。

补偿定理表明，

• 相关文章：戴维南定理。带有已解决示例的分步指南

补偿定理解释

要理解补偿定理，请看下图。

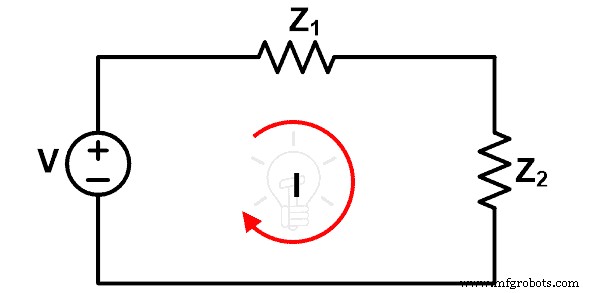
在该图中，电压源V是一个独立的电压源，两个阻抗Z1和Z2是线性或双边元件。因此，我们可以将补偿定理应用于该网络。通过回路的电流为 I。

现在，假设阻抗 Z2 增加了 ΔZ。由于这种变化，通过回路的电流发生了变化，它是 I'。新的电路图如下图所示。

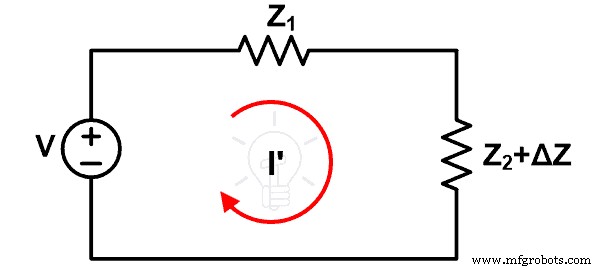
由于阻抗的变化，电流的变化由ΔI给出。

Δ我 =我 ——我

根据补偿定理的说法，我们可以直接计算出电流ΔI的变化。为此，我们需要修改电路。

第一个修改是，在改变阻抗的支路连接一个IΔZ值的电压源。并且这个电压源的极性与主电源的极性相反。新增的电压源VC称为补偿源。

VC =我 ΔZ

第二个修改是我们需要通过其内部阻抗去除旧电压源。如果我们考虑一个理想的电压源，在这种情况下，我们可以通过短路它的端子来移除这个电压源。经过这些修改，剩下的电路如下图所示。

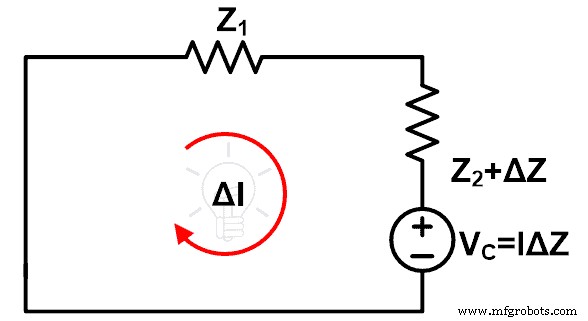
通过上面的电路求解，我们可以很容易的找到阻抗变化后电流的变化。

• 相关文章：诺顿定理。带有已解决示例的分步指南

补偿定理证明

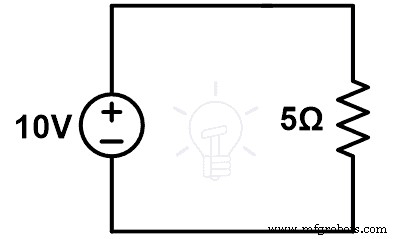
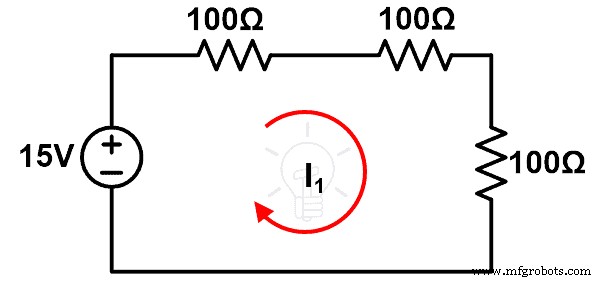
考虑图1中给出的电路。计算通过回路的电流（I）。

对图1应用KVL；

现在，我们假设阻抗 Z2 改变了 ΔZ。修改后的电路如图2所示。我们需要计算（I'）通过图2回路的电流。

对图2应用KVL；

由于阻抗的变化，回路电流的变化记为ΔI。 ΔI等于旧电流I与新电流I'之差。

Δ我 =我 ——我

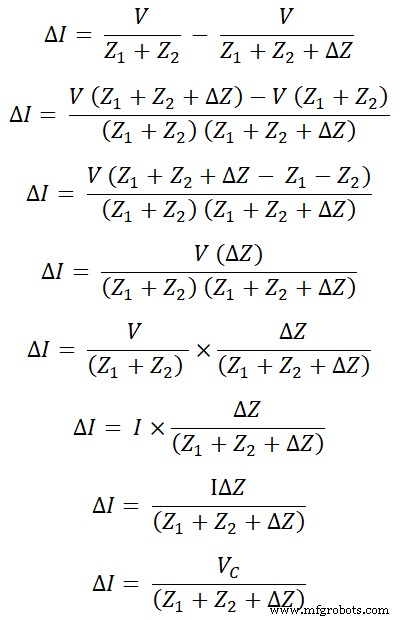
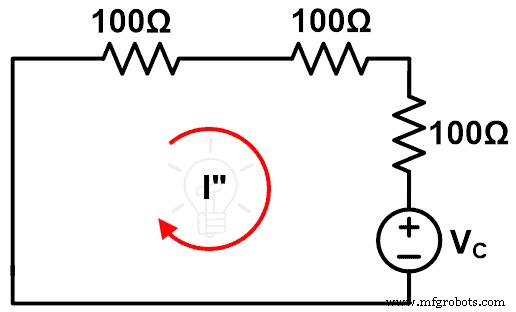
现在，考虑下图。

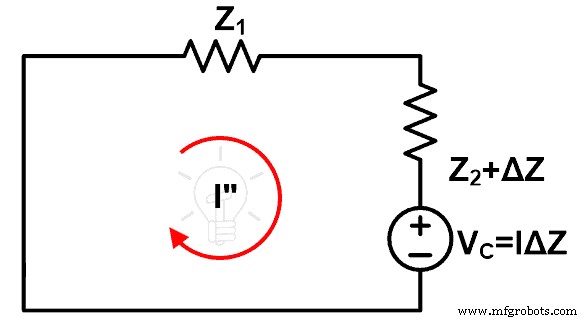
此图表示补偿定理执行后的电路。这里，通过短路去除原来的电压源（假设为理想电压源）。

我们会发现通过这个循环的电流就是I”。并将此电流与上面计算的电流进行比较。

要计算通过环路的电流，将KVL应用于上图。

VC =Z 1 我” +(Z 2 +ΔZ ) 我”

VC =我” (Z 1 + Z 2 + ΔZ )

我” =VC / (Z 1 + Z 2 + ΔZ )

我” =Δ我

由此证明修改后的电流变化（ΔI）与补偿定理计算的电流相同。

我们已经证明了补偿定理的陈述。

• 相关文章：叠加定理 - 带求解示例的电路分析

补偿定理实验

目标： 证明补偿定理，求电流变化。

设备： 电压表、电流表、电阻器、连接线、面包板、

电路图：

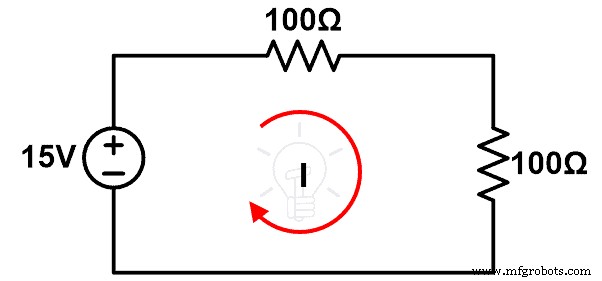
程序：

Step-1 使用面包板上的连接线连接组件，如图5所示。

Step-2 测量电流I。

Step-3 如图6所示连接组件。在这里，我们连接了一个额外的电阻。

Step-4 测量电流I1。

Step-5 根据 I 和 I1 的值计算电流变化 (ΔI)。

Step-6 如图7所示连接组件。本电路为补偿电路。

Step-7 测量电流I”。

Step-8 比较电流变化 (ΔI) 与 I”。

实验表：

高级没有。	我	我 1	Δ我	我”
1

结果：

通过比较电流I''的值与ΔI，我们可以证明补偿定理。

• 相关文章：米尔曼定理 - 分析交流和直流电路 - 示例

补偿定理示例

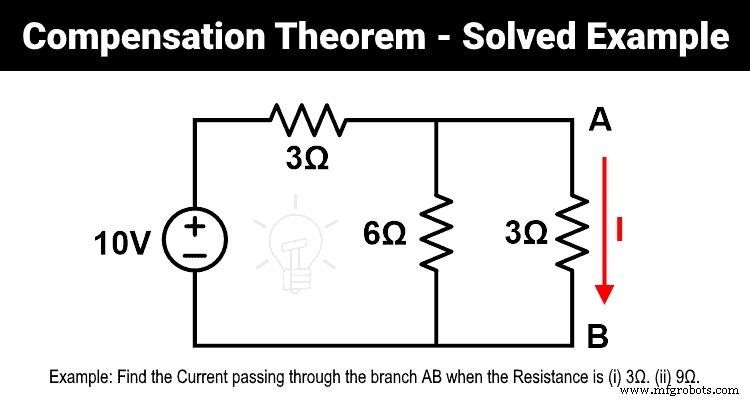
Example-1

• 1) 求电阻为3Ω时通过支路AB的电流。
• 2) 3Ω电阻变为9Ω时，利用补偿定理求通过AB支路的电流。
• 3) 证明补偿定理。

Answer-1

如图所示，6Ω和3Ω电阻并联。并且这个并联组合是串联了一个3Ω的电阻。因此，等效电阻为；

R 等式 =6 | | 3+3

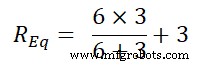
R 方程 =2 + 3

R Eq =5Ω

根据欧姆定律；

10 =我 (5)

我 =10 ÷ 5

我 =2个

现在，我们需要找到当前经过分支AB的路径。所以，根据电流分频器规则；

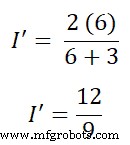
我' =1.333 A（或 3/4 A）

• 相关文章：替换定理 - 带求解示例的分步指南

Answer-2

我们需要将3Ω电阻换成9Ω电阻。根据补偿定理，我们需要在 9Ω 电阻上串联一个新的电压源。而这个电压源的值为；

VC =我' ΔZ

在哪里，

ΔZ =9 – 3 =6 Ω 和 I' =4/3 A（或 1.333 A）

VC =(4/3A) x 6Ω

VC =8 V

修改后的电路图或补偿后的电路图如下图所示。

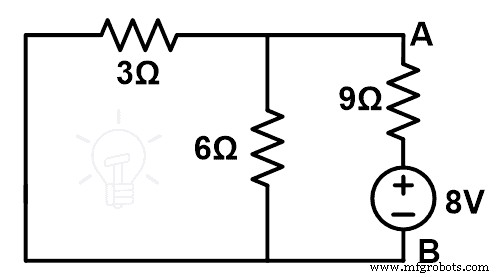
现在，我们将找到等效电阻。这里，3Ω和6Ω电阻并联。而这种并联组合是串联一个9Ω的电阻。

请求 =3 | | 6+9

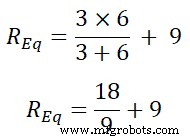
请求 =2 + 9

请求 =11Ω

现在，根据欧姆定律；

V =ΔI R

8 =ΔI (11Ω)

Δ我 =8 ÷ 11

Δ我 =0.7272 A

所以，根据补偿定理；电流变化为0.7272A。

• 相关文章：Tellegen 定理 - 求解示例和 MATLAB 仿真

Answer-3

我们要证明补偿定理。因此，我们在给定示例中使用 9Ω 电阻计算电流。

修改后的电路图如下图所示。

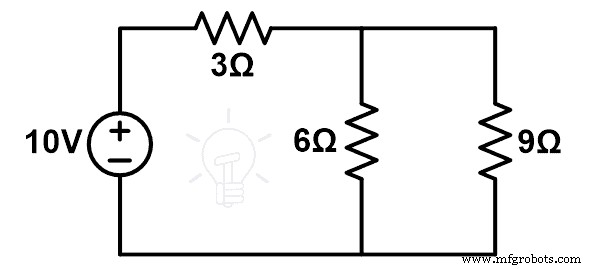
这里9Ω和6Ω电阻是并联的，这个并联组合是和3Ω电阻串联的。

等效电阻等于；

请求 =9 | | 6+3

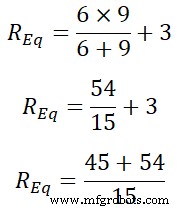
请求 =99 ÷ 15

请求 =6.66Ω

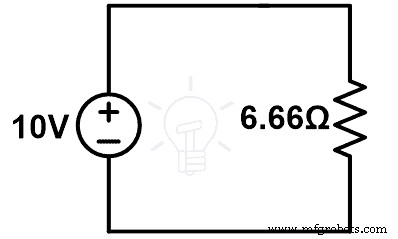
从上图看；

10 =我 (6.66)

我 =10 ÷ 6.66

我 =1.5151 元

按照当前的分隔规则；

我” =0.6060A

Δ我 =我' ——我”

Δ我 =(4/3A) – 0.6060

Δ我 =1.333A – 0.6060

Δ我 =0.7273 A

由此证明，补偿定理计算的电流变化与原电路计算的电流变化相同。

• 相关文章： 交流和直流电路的最大功率传输定理
  

Example-2

在下面的电路中，用补偿定理求出3Ω电阻换成7Ω电阻时电流的变化。并证明补偿定理。

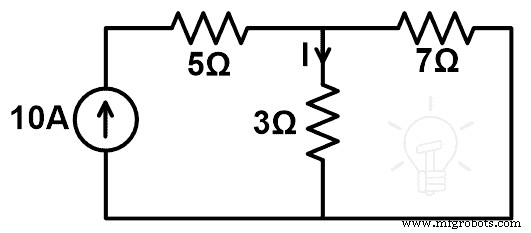
上述网络仅由电阻和独立的电流源组成。所以，我们可以将补偿定理应用于这个网络。

在此图中，网络由电流源供电。现在，我们需要找到通过 3Ω 电阻支路的电流。可以使用 KCL 或 KVL 找到该电流。但是在这里，这个电流可以很容易地通过分流规则找到。

因此，按照当前的分隔规则；

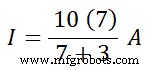
我 =70 ÷ 10 A

我 =7个

在原来的3Ω电阻网络中，通过该支路的电流为3A。现在，我们需要将此电阻从 3Ω 更改为 7Ω。由于此修改，通过该分支的电流将被更改。我们将通过补偿定理找到电流的这种变化。

为此，我们需要建立一个补偿网络。为了制作补偿网络，我们需要通过短接电压源和开路电流源来移除网络中所有可用的独立电源。

在这个网络中，只有一个电流源可用。我们假设电流源是一个理想的电流源。因此，我们不需要添加内阻。

我们需要在补偿电路中进行的第二个修改是添加一个额外的电压源。而这个电压的值为；

VC =我 ΔZ

VC =7 × (7 – 3)

VC =7 × 4

VC =28 伏

补偿网络如下图所示。

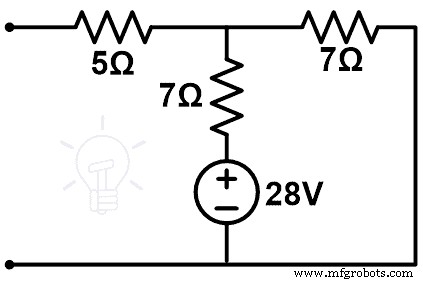
这个图只有一个循环。而通过7Ω支路的电流会给我们电流的变化（ΔI）。

Δ我 =VC ÷ (7+7)

Δ我 =28 ÷ 14

Δ我 =2个

为了证明补偿定理，我们将在连接一个7Ω电阻的电路中找到电流。修改后的电路图如下图所示。

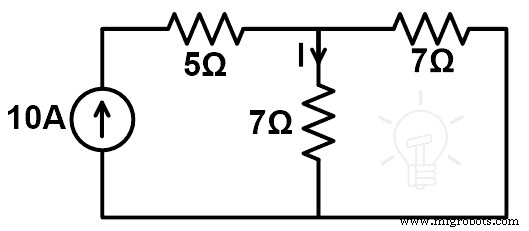
我” =(10 (7)) ÷ (7 + 7)

我” =70 ÷ 14

我” =5 个

通过应用当前分隔规则；

要找到电流的变化，我们需要从通过原始网络的电流中减去这个电流。

Δ我 =我 ——我”

Δ我 =7 - 5

Δ我 =2个

由此，我们证明了补偿定理。

相关电路分析教程：

• SUPERNODE 电路分析 - 逐步解决示例
• SUPERMESH 电路分析 - 逐步解决示例
• 基尔霍夫电流和电压定律 (KCL &KVL) |解决的例子
• 克莱默规则计算器 - 电路的 2 和 3 方程系统
• 惠斯通电桥——电路、工作、推导和应用
• 电气和电子工程计算器
• 5000 多个电气和电子工程公式和方程式